
To go directly a particular section of this paper, click on a section title below.
| 1. The models |
| 2. The limitations |
| 3. Visual abduction |
| 4. The demise of SK54 |
| 5. Coherence |
| 6. Conclusion |
Abstract
This paper discusses abductive reasoning---that is, reasoning in which explanatory hypotheses are formed and evaluated. First, it criticizes two recent formal logical models of abduction. An adequate formalization would have to take into account the following aspects of abduction: explanation is not deduction; hypotheses are layered; abduction is sometimes creative; hypotheses may be revolutionary; completeness is elusive; simplicity is complex; and abductive reasoning may be visual and non-sentential. Second, in order to illustrate visual aspects of hypothesis formation, the paper describes recent work on visual inference in archaeology. Third, in connection with the evaluation of explanatory hypotheses, the paper describes recent results on the computation of coherence.
There has been an explosion of recent work in artificial intelligence that recognizes the importance of abductive reasoning---that is, reasoning in which explanatory hypotheses are formed and evaluated. Many important kinds of intellectual tasks, including medical diagnosis, fault diagnosis, scientific discovery, legal reasoning, and natural language understanding have been characterized as abduction. Appropriately, attempts have been made to achieve a more exact understanding of abductive reasoning by developing formal models that can be used to analyze the computational properties of abductive reasoning and its relation to other kinds of inference. Bylander et al. [4] have used their formal model to analyze the computational complexity of abduction and show that in general it is NP-hard. Konolige [16] has used a similar formal model to derive results concerning the relation between abductive reasoning and Reiter's model of diagnosis [16]. While these formal results are interesting and useful, it would be unfortunate if researchers were to conclude that the analyses of Konolige, Bylander et al. have provided a precise understanding of abductive reasoning. We shall discuss numerous important aspects of inference to explanatory hypotheses that are not captured by one or both of the formalisms that these authors have proposed. In particular, we show how these models do not adequately capture abductive discovery using representations that are pictorial, and we argue that abductive evaluation should be conceived in terms of coherence rather than deduction.
Definition 1.1 Let L be a first order language. A simple causal theory is a tuple {C,E,Sigma} where:
1. C, a set of sentences of L, are the causes;Definition 1.2 Let {C,E,Sigma} be a simple causal theory. An explanation of a set of observations O subset E is a finite set A subset C such that:2. E, a set of sentences of L, are the effects;
3. Sigma, a set of sentences of L, is the domain theory.
1. A is consistent with Sigma;Definition 1.3 An abduction problem is a tuple {Dall,Hall,e,pl} where:2. Sigma cup A vdash O;
3. A is subset-minimal over sets satisfying the first two conditions, i.e., there is no proper subset of A consistent with Sigma that implies O.
Bylander and his colleagues offer a similar definition:
1. Dall is a finite set of all the data to be explained;2. Hall is a finite set of all the individual hypotheses;
3. e is a map from all subsets of Hall to subsets of Dall;
4. pl is a map from subsets of Hall to a partially ordered set representing the plausibility of various hypotheses.
A set of hypotheses H is an explanation if it is complete and parsimonious, i.e., if e(H) = Dall, and no proper subset of H explains all the data that H does.
The similarities between these two sets of definitions are clear. Konolige's [16] causes correspond to Bylander et al. [4] hypotheses; Konolige's effects correspond to Bylander et al.'s data. Konolige's requirement that a set of causes be subset-minimal is the same as Bylander et al.'s requirement that a set of hypotheses be parsimonious. (Peng and Reggia [21] call the same property irredundancy.) Bylander et al. [4] go beyond Konolige in requiring an explanation to explain all the data and in adding a plausibility ordering on hypotheses. On the other hand, their definition is more general than Konolige's in not restricting data and hypotheses to sentences.
These definitions usefully capture much of what is central in abductive reasoning, particularly the goal of assembling a set of hypotheses (causes) that provide good explanations of the data (effects). But each of them oversimplifies abductive reasoning in several important respects.
In 1948, Hempel and Oppenheim proposed what has come to be known as the deductive-nomological model of explanation [12]. On this model, an explanation is a deductive argument in which a sentence representing a phenomenon to be explained is derived from a set of sentences that describe particular facts and general laws (nomos is Greek for law). This model provides a good approximation for many explanations, particularly in mathematical physics. But it is evident that the deductive model fails to provide either necessary or sufficient conditions for explanation. See [15] for a comprehensive review of several decades of philosophical discussions of the nature of explanation, and [18] for application to artificial intelligence.
First, there are many explanations in science and everyday life that do not conform to the deductive model. Hempel himself discussed at length statistical explanations in which what is explained follows only probabilistically, not deductively, from the laws and other sentences that do the explaining. Many critics have argued that explanations in such fields as history and evolutionary biology rarely have a deductive form. In both philosophy and AI, researchers have proposed that many explanations can be understood in terms of applications of schemas that fit a phenomenon into a pattern without producing a deductive argument. (For a review of different approaches to explanation in these fields, see [27, 28].) For example, a Darwinian explanation of how a species evolved by natural selection applies a general pattern that cites biological mechanisms and historical facts to suggest how an adaptation might have come about. But the historical record is too sparse and biological principles are too qualitative and imprecise for deductive derivation. Thus Konolige's use of deduction in his characterization of abduction arbitrarily excludes many domains in which hypotheses are formed and evaluated but do not provide deductive explanations.
Second, the deductive model of explanation does not even provide sufficient conditions for explanation, since there are examples that conform to the model but do not appear to constitute explanations. For example, we can deduce the height of a flagpole from information about its shadow along with trigonometry and laws of optics. But it seems odd to say that the length of a flagpole's shadow explains the flagpole's height. Konolige's subset-minimality requirement serves to rule out some of the cases of irrelevance that philosophers have discussed, for example the explanation that a man is not pregnant because he takes birth control pills. But other examples such as the flagpole show that some additional notion of causal relevance is crucial to many kinds of explanation, and there is little hope of capturing this notion using logic alone. Contrast Pearl's [20] work on Bayesian networks and Peng and Reggia's [21] model of abduction which employ ineliminably intuitive notions of causality. A general model of abduction requires an account of explanation that is richer than deduction.
Just as Bylander et al. assume that only data are explained, so Konolige assumes that only observed effects are explained by derivation from causes. But as both Bayesian and explanatory coherence analyses allow, causes are often themselves effects and assessment of overall acceptability of explanatory hypotheses must take this into account.
Suppose you return to your car at the shopping center and find a big scratch on one door. Naturally, you wonder how it happened and start to generate hypotheses to explain how the scratch came to be. Your abductions may be purely verbal, if you start to apply rules such as ``If a car door is opened and collides with another car door, the latter door is scratched.'' You could then verbally abduce that some other car door was opened and collided with yours. But a mode of thinking that is natural for many people is to perform the same kind of thinking pictorially. You can form a mental image of a car driving up beside yours and then its driver opening a door that scratches yours. Here the explanation is a kind of mental movie in which you imagine your door being scratched. The abductive inference that the accident happened this way involves a mental picture of the other car's door hitting yours. Such pictures provide an iconic representation of the event that you conjecture to have happened, since the picture you form resembles the hypothesized event in a much more direct way than a verbal/sentential representation would. Whenever our knowledge of how things work in the world involves dynamic pictorial representations, these representations can be used to generate iconic explanations of what occurs. Many scientists have reported that images played a crucial role in their most creative thinking: the most eminent include Bohr, Boltzmann, Einstein, Faraday, Feynman, Heisenberg, Helmholtz, Herschel, Kekule, Maxwell, Poincare, Tesla, Watson, and Watt.
Performing abduction visually may have strong cognitive advantages. With verbal representations such as rules, it may be necessary to search through many possible inferences before finding a plausible explanatory hypothesis. But a picture of a situation may immediately suggest a likely cause, if it vividly displays factors that are spatially contiguous and therefore more likely to be causally relevant. Artificial intelligence is still very limited in its ability to use such visuospatial information, although progress is being made in the direction of imagistic representations. Glasgow has argued for the importance of spatial reasoning in AI and proposed a representational scheme based on 3-dimensional arrays [9, 8]. Graphs provide visual representations that are more flexible than arrays [5, 30], so to show how abduction can be visual yet nevertheless amenable to formal treatment, we will now discuss graph grammars.
A simple graph can be thought of as a purely algebraic structure consisting of a set of vertices and edges, but uses of graphs often exploit their visual character. When we draw a graph representing, for example, the paths between various cities, we get a diagram or mental representation of the routes between cities that resembles the actual roads. The mathematical structure of a graph naturally translates into a graphical diagram that resembles what it represents much more directly than a set of sentences would. Graph grammars consist of sets of production rules that differ from standard verbal productions in that the left-hand sides (conditions) and right-hand sides (actions) are represented as graphs rather than as verbal structures [7, 14, 19]. A graphical production can be interpreted as saying that if you have one graphical structure and you apply a transformation to it, then you get another graphical structure. For abduction purposes, we can think of the right-hand side of a graph production as providing a visual representation of something to be explained, and the left-hand side and the transformation as providing a possible visual explanation.
(Graphic not available)
Figure 1. Graph representation of a Lego block.
To be more concrete, consider children's interlocking Lego blocks. We can represent each block as a graph whose vertices are connectors and sockets, where the connectors on one block fit into the sockets on another block. Figure 1 gives a graph for a simple 4-connector block, with 8 vertices and 12 edges. Transformations possible for Lego blocks include stacking one on top of the other, which produces a new structure in which the connectors on the bottom block go into the sockets on the top block. A graphical production representing this would have a left-hand side of two unconnected graphs and a transformation that produced new edges connecting the appropriate sockets and connectors, producing a new connected graph with a total of 16 vertices and 28 edges, including 4 new ones.
Given such a production, we could explain the existence of a tower consisting of two blocks by hypothesizing that there were two independent blocks that had been transformed by joining. Abduction is then visual because the representations of both what gets explained and what does the explaining use structures that resemble what they represent.
Let us now state this more formally.
Definition 3.1 A graph G is a tuple {V,E} where:
Definition 3.2 A graph grammar Gamma is a finite set of productions P, where a production is a tuple {Gl,Gr,T} such that:
- V is a set of vertices;
- E subset (V times V) is a set of edges.
Definition 3.3 A graph-grammatical abductive explanation of a target graph G^t is a hypothesis graph G^h such that there is a set of productions in P whose successive transformations transform G^h into G^t.
- Gl is the left-hand side;
- Gr is the right-hand side;
- T is the embedding transformation that specifies the relations between the vertices and edges of Gl and Gr.
Intuitively, the hypothesis graph G^h provides an explanation of the target graph G^t by virtue of a series of transformations that show how the target graph can be produced from the hypothesis graph.
Graph grammars are not the only possible basis for visual abduction. Leyton [17] presented a ``process grammar'' that could be used to infer the causal history of objects from their shapes. This grammar contains such productions as one that can be interpreted: ``If a shape is squashed, it will indent.'' If the shapes and the processes of squashing and indenting are represented pictorially, then the inference that explains a shape's indentation by its having been squashed is an instance of visual abduction.
This paper does not attempt to present a general theory of visual abduction, but rather some instances that show the limitations of current formal models of abductive reasoning. A fully general characterization of abduction would have to allow representations of causes and effects that are pictorial as well as ones that are sentential. It would also have to admit forms of explanation that centrally employ visual transformations as well as ones that employ deduction and other verbal processes. In addition, we should not rule out the possibility of a multimodal theory of abduction that includes non-visual, non-verbal representations involving smell, touch, and emotion. For example, there are some diseases that physicians can diagnose based on a patient having a particular odor. The need for a multimodal theory is illustrated below with an archaeological example.

Figure 2. The skullcap SK54 with notches indicated by white arrows [2, p. 1117]

Figure 3. The abduced fate of SK54 in the jaws of a leopard [2, p. 1118]
For example, in 1949 excavations of a cave at Swartkrans in South Africa yielded, among much other debris, the skullcap of an australopithecine (thereafter designated SK54). The distinctive features of this skullcap consisted of two notches, one on either side of the centerline, which had obviously been driven into the back of the skull by two pointed objects when the creature was still alive [2]. SK54 is pictured in figure 2, with the notches indicated by the two arrows. At first it was supposed that the notches had been inflicted by two separate blows from a weapon wielded by another hominid, because each notch had been made at divergent angles from the centerline [1]. This hypothesis accorded well with the prevailing theory that human evolution had been driven by murder and cannibalism---Dart's [6] ``killer ape'' hypothesis.
However, an alternative explanation has been offered by Brain [2]. Noting that the lower canine teeth of leopards diverge and are about the right distance apart, Brain hypothesized that the notches had been created by a leopard which had taken the australopithecine's head in its mouth, as dramatically illustrated in figure 3. Indeed, a fossil leopard jaw from the same site (SK349) fits the notches fairly well and shows that the hypothesis is a plausible one; see also [3]. This is shown in figure 4.
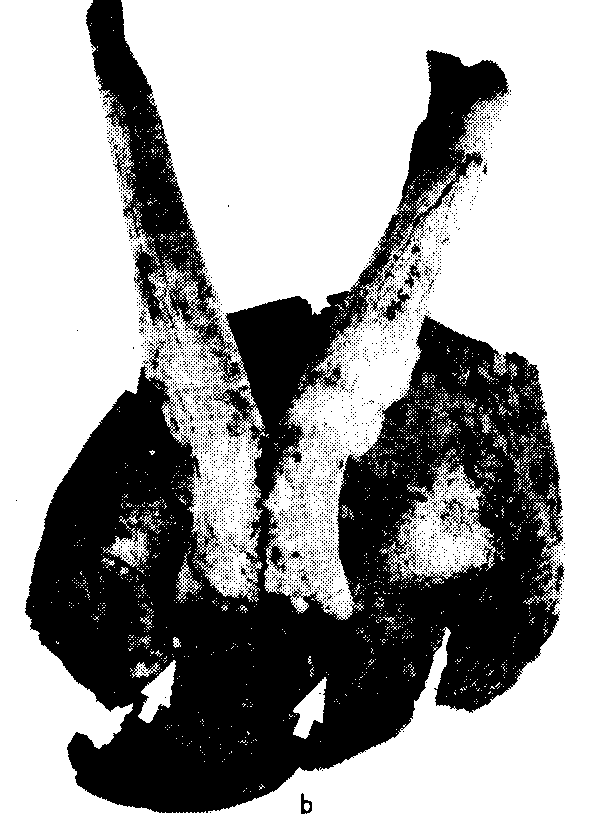
Figure 4. Fossil leopard jaw SK349 fitted into the notches of SK54 [2, p. 1117]
This explanation of the notches in SK54 also accords with several other facts about the debris in the Swartkrans cave. The entrance to the cave was a vertical shaft when the australopithecine remains were deposited and those remains are mostly comprised of skull fragments. Similar shaft caves in the area today are frequented by leopards which use the trees which grow around the entrances as places to safely consume prey out of the reach of hyenas. Since leopards tend to destroy the skeletal material of their primate prey with the exception of the skulls, the leopard-predator hypothesis would also explain why the australopithecine remains are mostly skull fragments---the skulls would simply have fallen from the trees and into the cave shafts [2]. This scenario, leopard predation of early hominids, is much different from the ``killer ape'' scenario favored by Dart.
Brain's leopard hypothesis exemplifies the use of visual abduction. The target of explanation---the unusual notches in the skullcap SK54---are highly visual in nature, consisting in their placement, depth, and direction. The hypothesis reconstructs the vital moment in the history of an unfortunate hominid, when its head was clenched in the jaws of a leopard to produce the notches. Because the relevant data are spatial, the hypothesis is most parsimoniously captured visually, as in figure 3, and may well have first occurred to Brain as just such a mental picture. The hypothesis thus abduced was then corroborated by further evidence of fossil leopard jaws and the feeding habits of modern leopards. Thus, this example illustrates that visual abduction fits the expanded criteria for abduction discussed in section 2.
Let E be a finite set of elements ei and C be a set of constraints on E understood as a set (ei, ej) of pairs of elements of E. C divides into C+, the positive constraints on E, and C-, the negative constraints on E. With each constraint is associated a number w, which is the weight (strength) of the constraint. The problem is to partition E into two sets, A (accepted) and R (rejected), in a way that maximizes compliance with the following two coherence conditions:
1. if (ei, ej) is in C+, then ei is in A if and only if ej is in A;Let W be the weight of the partition, that is, the sum of the weights of the satisfied constraints. The coherence problem is then to partition E into A and R in a way that maximizes W.2. if (ei, ej) is in C-, then ei is in A if and only if ej is in R.
To understand abduction as a coherence problem, we need to specify the elements and the constraints. The elements are representations of causes and effects; in line with our discussion of visual abduction, we will allow the representations to include both sentential and nonsentential representations such as visual ones. The major positive constraint on abduction is that if one element explains another, then there is a symmetric positive constraint between them. In accord with the first of the two coherence constraints above, this will have the effect that if the explaining element and the explained element will tend to be accepted or rejected together. If, as often happens, more than one element is required to explain another element, the weight on the constraint between each explaining element and the explained element can be less than if there were only one explaining element, in keeping with the theory of simplicity of Thagard [28].
Two sorts of negative constraint are possible. If two elements contradict each other, then there is a symmetric negative constraint between them, but there is also a negative constraint if two elements offer competing explanations of the same fact [28]. Deciding which explanatory hypotheses to accept and which to reject is a matter of maximizing compliance with the two coherence conditions. Computationally, this is a very difficult problem and no tractable algorithm for solving it is available, although various approximation algorithms work quite well [29].
Our account of abduction as a coherence problem avoids all the limitations we discussed in section 2. We assume that the relation between elements is explanation, not deduction. Elements can explain other elements which explain other elements, so hypotheses can be layered and give rise to complex chains of constraints. Abduction is not defined in terms of a fixed set of elements but allows the possibility of creation of new elements that produce a new assessment of coherence. New hypotheses need not be consistent with existing ones, nor need the facts be completely explained. Maximizing coherence involves explaining as much as possible (positive constraints) and being as consistent as possible (negative constraints), but perfection is not to be sought in abductive reasoning. We are not urging inconsistency as a general epistemological strategy, only noting that it is sometimes necessary to form hypotheses inconsistent with what is currently accepted in order to provoke a general belief revision that can restore consistency.
Reducing the weights on constraints when explanation is accomplished by multiple hypotheses allows a complex assessment of simplicity. Finally, since elements can be visual or other nonverbal kinds of representation, we have transcended the limitation of abductive reasoning to sentences.
Thanks to important formal results such as the theory of NP-completeness, formal methods have achieved much well-deserved prestige in computer science and artificial intelligence. But an oversimplified formalization can distract from important aspects of the kinds of reasoning that underlie intelligence. Graph grammars and other techniques for visual representation offer the prospects of developing more general accounts of the nature of abductive reasoning, which should be construed not as a deviant form of deduction, but as a coherence problem.
[2] C. K. Brain. New finds at the Swartkrans australopithecine site. Nature, 225:1112-9, 1970.
[3] C. K. Brain. The hunters or the hunted? An introduction to African cave taphonomy. The University of Chicago Press, Chicago, Ill., 1981.
[4] T. Bylander, D. Allemang, M.C. Tanner, and J.R. Josephson. The computational complexity of abduction. Artificial Intelligence, 49:25-60.
[5] J. Y. Ching. Computational imagery: An alternative framework. Ph.D. thesis proposal, Pattern Analysis and Machine Intelligence Lab, University of Waterloo, Waterloo, On., May 1994.
[6] R. A. Dart. The predatory transition from ape to man. International Anthropological Linguistic Review, 1(4):201-18, 1953.
[7] H. Ehrig, H. J. Kreowski, and G. Rozenberg, editors. Graph-grammars and their application to computer science:4th international workshop, number 532 in Lecture notes in computer science, Berlin, Germany, March 1990. European Association for theoretical computer science, Springer Verlag.
[8] J. I. Glasgow. The imagery debate revisited: A computational perspective. Computational Intelligence, 9:309-33, 1993.
[9] J. I. Glasgow and D. Papadias. Computational imagery. Cognitive Science, 17930:355-394, 1992.
[10] T. A. Goudge. The thought of C. S. Peirce. University of Toronto Press, Toronto, On., Canada, 1950.
[11] C. Hartshorne and P. Weiss, editors. Collected papers of Charles Sanders Peirce. Harvard University Press, Cambridge, Mass., U.S.A., 1958. Volumes 7-8 edited by A. Burks.
[12] C. G. Hempel. Aspects of scientific explanation. The Free Press, New York, N.Y., 1965.
[13] J.R. Hobbs, M. Stickel, D. Appelt, and P. Martin. Interpretation as abduction. Technical Note 499, AI Center, SRI International, 333 Ravenswood Ave., Menlo Park, CA 94025, December 1990.
[14] C.V. Jones. An integrated modeling environment base on attributed graphs and graph-grammars. Decision Support Systems: The international journal, 9(10):255-72, 1991.
[15] P. Kitcher and W. Salmon. Scientific explanation. University of Minnesota Press, Minneapolis, M.N., 1989.
[16] K. Konolige. Abduction versus closure in causal theories. Artificial Intelligence, 52:255-72, 1991.
[17] M. Leyton. Inferring causal history from shape. Cognitive Science, 13:357-87, 1989.
[18] D. V. McDermott. A critique of pure reason. Computational Intelligence, 3:151-60,1987.
[19] M. Nagl. Formal languages of labelled graphs. Computing, 16:113-37, 1976.
[20] J. Pearl. Probabilistic reasoning in intelligent systems. Morgan Kaufman, San Mateo, CA, 1988.
[21] Y. Peng and J. Reggia. Abductive inference models for diagnostic problem solving. Springer Verlag, New York, N.Y., 1990.
[22] R. Reiter. A theory of diagnosis from first principles. Artificial Intelligence, 32:57-95, 1987.
[23] D. D. Roberts. The existential graphs of Charles S. Peirce. Mouton, The Hague, 1973.
[24] C. Shelley. Visual abductive reasoning in archaeology. Under review, 1996.
[25] P. Thagard. Computational philosophy of science. MIT Press, Cambridge, Mass., 1988.
[26] P. Thagard. Explanatory coherence. Behavioral and Brain Sciences, 12:435-67, 1989.
[27] P. Thagard. Philosophical and computational models of explanation. Philosophical Studies, 64:87-104, 1991.
[28] P. Thagard. Conceptual revolutions. Princeton University Press, Princeton, N.J., 1992.
[29] P. Thagard and K. Verbeurgt. Coherence. Under review.
[30] A. Wong, S. Lu, and M. Rioux. Recognition and shape synthesis of 3-D objects based on attributed hypergraphs. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11(3):279-90, Jun 1989.