|
Approach to a model of the aging phenomenon
by |
|
J.-P. VANBREMEERSCH and A.C. EHRESMANN
from the "Mémoire de Capacité en Gérontologie" (Dr VANBREMEERSCH, Amiens 1992), abstracted in "IXth International Congress of Cybernetics & Systems" (New Delhi 1993) |
INTRODUCTION
Numerous physiological theories of aging have been proposed (these are reviewed in Part II). Most of these theories approach the problem in an essentially local manner: Orgel's theory of catastrophic errors due to the malfunctioning of enzymes; theories implicating mutations, either within the framework "of an aging program", or in a stochastic manner; Hayflick's theory proposing a limitation in the number of cell duplications encoded in the genome; several theories implicating free radicals; theories of Verzar and Robert concerning the involvement of extracellular matrices or other theories emphasizing, for example, the predominance of immune aging or the slowing down of biological rhythms.
Each of these theories stresses the role of a particular factor intervening at a certain level and the resulting pathological consequences. But they do not allow for a combination of the different phenomena observed in the course of aging.
In this study, we shall use a mathematical model for complex systems with a hierarchy of internal regulation centers that permits a more unified approach to the phenomenon of senescence as a consequence of a dialectics between these centers due to the systemic nature of the levels and their different timescales. Aging for an organism is reduced to a phenomenon of progressive desynchronization between these centers, resulting from the reduction in stability of the complex components (increase in turnover or acceleration of degradation) and the increase in transmission delays for functioning and repair. We'll speak of a "cascade of de/resynchronizations".
This temporal imbalance thus accounts for the constraints imposed by the interplay between predetermined strategies that have limited capacities for repair, and the external stochastic disturbances that have an unpredictable rhythm and intensity.
I. AGING WITHIN THE THEORETICAL FRAMEWORK OF AN EVOLUTIVE HIERARCHICAL SYSTEM
Aging will be studied within the framework of a mathematical model for autonomous, open, natural systems such as biological or sociological systems (introduced in Ehresmann & Vanbremeersch 1987, 1989, 1990, 1991, 1992), based on the theory of categories. This recent branch of mathematics (cf. Mac Lane 1971) offers a relational approach that is more qualitative than quantitative and better adapted to the study of a complex system, that is, one where the components are organized in levels of an increasing hierarchical order, overlapping on a structural and functional level.
A/ Notion of a complex system
A natural complex system, for example an animal's body, presents different levels of increasing order of complexity with their components being atoms, macromolecules, intracellular structures, cells, tissues, organs... An object is said to be complex if it itself has an internal organization at a lower level; for example, a cell in relation to its organelles, a macromolecule in relation to its atoms.
1) Modeling of a system by a category
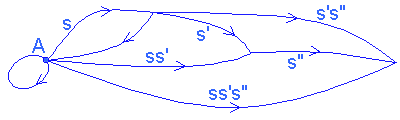
To model the internal organization of a system composed of its components and their relations, we use specific mathematical tools: a system is represented in the form of a graph, called a category, whose vertices or objects represent the components of the system, and the arrows, called links, correspond to the interactions between these components which may be of an informational or causal nature, energy transfers, or constraints linking these components. Between 2 objects, there can be several links or no link, and 'closed' links are accepted (of an object towards itself).
For example, in a cell, the components of an infracellular level will be cell organelles (cell membrane, nucleus, mitochondria, Golgi apparatus,...), the links between these components, constraints and topological relations, enzymatic or nucleotide messages...
The efferent links from a component represent more specifically its functional behavior or the commands it sends, the afferent links represent the data or constraints it receives.
To define the category, a law of composition between consecutive links (satisfying axioms of associativity and identity) must be added to operate a correlation on the chains of links. (For a study of categories, cf. MacLane 1971.)
FIGURE 1
|
|
|
CATEGORY |
NATURAL SYSTEM |
CATEGORY OF NEURONS |
|
objects |
Components |
neurons |
|
Arrows between objects (or links) |
interactions (constraints, transfers of information or energy, causality) |
Multi-synaptic paths (classes of functionally equivalent synaptic paths) |
|
composition of links |
Transitivity of transfers |
concatenation |
|
2 successive links s and s' have the composite ss' and s(s's") = (ss')s" (associativity) |
2) Modeling of a complex object
This category represents the relational structure of the system; in the description of a hierarchical organization with increasing levels of complexity, we are led to differentiate its objects according to their complexity. Our aim is to be able to model this system by considering each object such as a cell both as a simple constituent of the more complex object that is a tissue, and as a whole complex object regrouping its constituents and their links. To thus formalize the complexity allows us to consider both sides of the same object at the same time and not to reduce the analysis to a single level.
a) Two basic ideas to represent a complex object
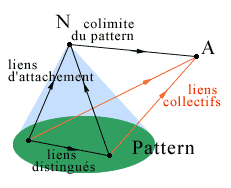
- In a category we consider families of linked objects, called patterns; a pattern consists of a family of objects, or components of the pattern, and some specific links between them that will be called the distinguished links of the pattern. These links will permit that the objects of the pattern have a concerted action towards an object outside the pattern, say A. More specifically, a family of individual links of each object of the pattern towards A forms a collective link of the pattern towards A when these links are correlated by the distinguished links of the pattern.
For example and more simply, let us consider the category associated with the organism. There is a pattern of immune cells whose links towards an outside object such as an antigen are correlated by a whole series of distinguished links between the various immune cells. The objects of the pattern will be the cells presenting the antigen (CPA), the various families of T-lymphocytes and B-lymphocytes. The distinguished links of the pattern will be either the links of proximity, corresponding to cell-to-cell contacts (for example presentation of the antigen by the CPA to a T-cell via the integrins, Springer 1990), or links representing more distant signals, especially those sent by several families of cytokines, small-sized polypeptides synthesized by the cells themselves and used as an intercellular message (interleukins, TNF, interferon, ...). The collective link towards the antigen A will be formed from the following family of individual links: for the cells presenting the antigen, binding of an epitope of this antigen on a receptor of their wall after binding to a major histocompatibility complex of the cell; for B-cells, release of antibodies or binding of the antigen on the immunoglobulin of the membrane; for cytotoxic T-cells, phagocytosis of the antigen. The immune cells have a concerted action as a result of the existence of the distinguished links in the pattern. The very great diversity of cytokines, their possibility of activity at very weak concentrations, their capacity to be in the activated or non-activated form, the fact that the same spectrum of activity corresponds to the same receptor confers to the class of cytokines the quality of a developed, specific, precise immunitary quasi-language (ASSIM 1991).
- Given a pattern, an object N is called the colimit of the pattern (or its gluing together or its inductive limit, MacLane 1971) if it represents the global behavior of the pattern towards any object A outside the pattern, that is, if its links towards the object A correspond exactly to the collective links of the pattern of linked objects towards A; in particular, there is a collective 'attachment link' from the pattern to its colimit. In a given category a pattern can have no colimit; we shall see further on that we can then add one by constructing a complexification of this category.
We take as an example a lower level in the immune system, no longer considering a cell population but a T-lymphocyte. Here we consider the mature T-cell as the colimit of the pattern whose components are the macromolecules involved in the immune activity within this cell, the regulatory genes of the DNA, the membrane receptor immunoglobulins, the genes of synthesis and some interleukins such as IL1, which has the capacity of autocrine activation and induction of lL2 secretion (which will activate cell duplication, ASSIM 1991). The distinguished links between these macromolecular components (intracellular mRNA-type messages or enzymatic messages) compel them to follow a concerted behavior towards the exterior, for example an antigen.
The coherence and constraints introduced by the distinguished links of the pattern may be measured by comparing the colimit of the pattern (the T-cell in the example above) and the simple sum of its components, that is, their juxtaposition without concerted functioning, forgetting the distinguished links. This comparison (by means of a 'comparison' link from the sum towards the colimit) would indicate how the properties of the colimit are different from those of its basic components, and explain how the complexification, that is, the formation of a complex object colimit of a pattern, allows for the emergence of new properties for this complex object with respect to its components (Ehresmann & Vanbremeersch 1987).
b) Hierarchy of complex objects
A hierarchical system can be described as a category where the objects are distributed in a finite number of levels of increasing complexity, the objects of a certain level being homogeneous between them, but more complex than those of the lower levels. More specifically, at any level n different from level 0, each object is the colimit of a pattern of linked objects of the level n-1 formed by its constituents of the level immediately below and the interrelations between these; and these constituents are themselves colimits of their organization of a lower level... (Ehresmann & Vanbremeersch 1987).
The generic example we'll have to consider is that of an organism with its components of various levels (atoms and molecules, macromolecules, infracellular structures, tissues and organs, large systems such as the immunitary system).
B/ Evolution of a hierarchical complex system
Up to now, we have only introduced ideas that permit a study of the state of the system at a given instant. As our purpose is to model the process leading a living organism to aging, we must introduce the idea of an evolutive system to understand the modifications of a biological system in the course of its own evolution, but also since it is open, progressively under the constraints and exchanges it has with the environment.
1) The system is evolutive
We define an evolutive system by: a set of instants delimiting its timescale, a category (hierarchical system) representing the state of the system at each of its instants, and a function of transition between the category at an instant t and that at an instant t' > t.
In the natural biological systems under consideration, the transition between two instants will be determined by operations such as: suppression or decomposition of certain objects (catabolism, for example), absorption of external elements (endocytosis), formation of complex objects by gluing new patterns (biosynthesis of macromolecules), or strengthening of preexisting patterns in a more coherent and structured association (as during learning when there is the formation of synchronous neural assemblies) or, conversely, reduction of the coherence of a pattern by the addition or loss of objects and/or modifications of links (result of the action of alkylating agents or radiation on DNA).
2) Transitions and complexification process
These operations are described in the complexification process of a category according to a strategy. A strategy on a category is the data of objects, links or colimits to suppress, external elements to absorb, patterns without colimit to glue together. The operation of complexification of the category (Ehresmann & Vanbremeersch 1987) permits to construct, by a categorical process, the most economic category resulting from the implementation of this strategy. In particular, it is possible to determine the 'good' links between the new objects (colimits of the patterns to be glued), and easily operate on them.
Thus, for a cell, the S phase of DNA synthesis ends with a complexification of the category modeling the cell with respect to the strategy of DNA replication, while correcting the eventual errors with the help of repair mechanisms.
The difficult problem to shape the evolution of the system will be that of the choice to make between a certain number of admissible strategies at a given time. We shall see further on that this choice will be made through internal regulation organs. But now we can consider the problem of aging.
3) First approach to aging
One of the marks of aging will be the increasing instability of the components that expresses a greater difficulty of the system to regain its equilibrium in case of aggression. It will be all the more dangerous when combined with an increase in the propagation delays of information between the components, the two processes being reciprocally magnified; this leads to a loss of relative synchronicities between the functioning of the system at different levels. We shall return to this problem later on; in this paragraph we propose only to measure this instability.
The problem for maintaining the homeostasis of a complex object comes from the progressive modification in time of its internal organization formed by its components at a lower level and their links.
Thus the components of a cell are continuously renewed even though the cell as such is conserved. The turnover of a population of proteins is measured by their half-life, which is the duration necessary for renewal of half the protein population. This half-life will be shortened when the population is unstable, that is, either if it rapidly increases (by new protein synthesis) or rapidly degrades (a large number of proteins become denatured).
We model this notion in a hierarchical evolutive system where an object of level n is colimit of the pattern of its linked components of level n-1. First we mention that we can generally remove some components and links of a pattern without changing its colimit; a subpattern of the pattern is said to be representative if it has the same colimit as the entire pattern.
To state that an object of level n retains its complex identity of level n-1 during a certain period signifies that the pattern formed by its components of level n-1 is not renewed in an essential manner during this period; more precisely, there is a subpattern of the pattern which remains representative of the whole pattern (thus retains the same colimit) during the entire period. A measure of the stability of a complex object will be given by its stability span, that is the largest period t during which this complex identity is maintained (Ehresmann & Vanbremeersch 1987). Naturally, t depends both on the object, its level and the date it is studied.
Indeed, let us consider a complex object at instant t, colimit of a pattern of level n-1. It is possible to find a subpattern representative of the pattern and remaining such at the next instant so that the colimit is preserved between t and t+1. Here the idea of the preceding instant is completely relative and depends on the timescale of the level which is observed; maintaining a representative subpattern between the two instants will not require the same timescale for a cell organelle or for an entire organ. In contrast, the loss of the complex identity is modeled as the absence of such a representative subpattern of the pattern studied between two remote instants: while there are representative subpatterns between t and t+1, between t+1 and t+2,..., t+k and t+k+1, on the contrary there is none between t and t+k+1. In this case the stability span t of the complex object at t will be less than k; it will be the largest number t where a representative subpattern can be found at t that is still representative at t+t.
By analogy, if the letters of a sentence are randomly changed at the rate of one per second, the sentence will continue to retain its significance up to an instant where it will no longer be understandable; but at each second, the difference is sufficiently small to not alter it in practice.
We designate by tn (or only t if no confusion is possible) the average time during which an object of level n retains its complex identity of the level n-1. As a general rule, the observations concern populations (cell, cellular ultrastructures, macromolecular or molecular components) for which we shall admit that this average tn is proportional to the usual quantifications of the half-life. This delay decreases if there is a rapid degradation of products, for example for the macromolecular level, if a certain population of proteins is denatured more rapidly, or if the DNA has undergone too many mutations.
The stability span t is an increasing function of the level; from the order of a minute for metabolites, it can go to several days at the cellular level. Its decrease is both a cause and an effect of aging, as proposed in some theories (cf. II). But we shall see that it is not sufficient to explain all the phenomena of senescence, and that the different propagation delays of the information within the system must intervene, as well as the periods of different cycles.
C/ Dynamic regulation of the system
1) Centers of Regulation and agents
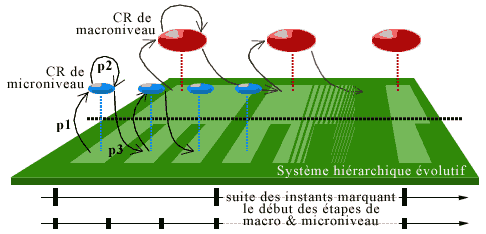
In open autonomous systems, the evolution of the system is controlled by a hierarchy of internal organs of regulation (consider the hierarchy of hormonal controls of the hypothalamus - pituitary gland - peripheral glands - target cells - intracellular effectors) assuring a functional control and permitting an adaptation of the state of the system to external and internal constraints.
In an evolutive system as we have defined above, these organs are modeled by the regulatory system, which is formed by a net of evolutive subsystems called centers of regulation or Coregulators (CR), each with its own timescale that consists of a sequence of instants. We suppose that at each hierarchical level there are one or more CRs. These CRs will operate as organs of observation, command and control at the same time. We shall first describe the situation relative to one CR, then their coordination/competition that will modulate the evolution of the entire system.
a) Landscape of the system for a CR
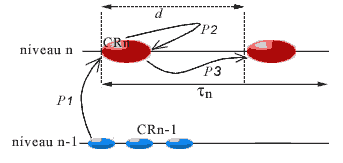
The time period (which can vary) that runs between two successive instants of the timescale of the CR corresponds to a step for this CR. The duration of steps increases with the level of complexity of the CR. For a cell, a step coincides with a cell cycle.
At each stage, the components of the CR, called its agents, form a certain 'image' of the system, which we call their actual landscape. The agents will only have certain information about the system; for example, those coming from an object B of the system will consist of the links from B towards the agents, called aspects of B for the CR. Because of their links in the CR, the agents 'communicate between them' all the aspects that they can receive from the system. This is modeled by the construction of a new category, the actual landscape of the system for the CR (Ehresmann & Vanbremeersch, 1989).
Thus, the landscape of the organism for a cell at a given instant will be determined by a few biochemical phenomena affecting its components and triggered by the binding to the membrane of a cellular mediator (for example, hormonal), by changes in the concentration of this or that oligoelement, etc... A T-lymphocyte will only know an antigen through the complex epitope+HML that a macrophage presents to it, or even only by means of some IL1.
It can be said that the landscape is the representation that the agents form of the system at a given date. There is a loss of information for the CR, not accessible to it, but externally measurable (by a functor 'distortion' from the landscape to the system).
b) Development of a regular step for a CR
The agents will play their role as regulatory agents on the data obtained in the landscape. When the landscape is changed under the effect of internal or external constraints, a new step is triggered that consists of:
- reception and analysis of the information in the landscape,
- search for admissible strategies on the landscape, then among these, choice and realization of a strategy,
- evaluation of the result (by comparing the anticipated landscape with the new landscape after the change).
In the case the result is inadequate, a new strategy is chosen and applied until the required result is obtained and homeostasis is restored in the landscape of the CR. When the result is obtained before the end of the step, it terminates by a period of rest.
But there is the risk that the step be interrupted prematurely when the strategy chosen cannot be applied (for example, if the necessary components have been destroyed), or if no strategy is possible for the CR (as in the case of paralysis of the repair systems). In this case we say that a fracture occurs in this landscape, initiating a new step.
2) Regulatory System
Up to now we have described the regulation at the level of a single CR. But we stated that there is a complete hierarchy of CRs (forming the Regulatory System; cf. Ehresmann & Vanbremeersch 1990 1991). Such a hierarchy of CR models, for example, the control mechanisms of DNA replication; we shall see its importance for the phenomenon of senescence.
To simplify, we consider the case of a bacterium, but the situation would be similar for higher organisms. In our model, the replication of the bases of the DNA chain is carried out under the control of a regulatory system consisting of two levels of CRs (cf. Ehresmann and Vanbremeersch 1987):
- a microlevel whose (micro)agents are the gene activating the replication, that is, the genes synthesizing the DNA polymerase (pDNA), the genes controlling the SSB protein (which permits the separation of the bases following those replicated by pDNA), the genes encoding the synthesis of patrol enzymes that correct an eventual defect in base pairing before their replication;
- a macrolevel where the agents are operons, functional combinations of more complex genes such as the SOS system (Radman 1975), normally inhibited by the LexA protein (Little & Mount 1982), and protein populations (SSB, RecA,...). Under certain conditions these will permit unblocking a situation of paralysis of the microlevel (we shall return to the play between these two CRs later).
The choices of strategies of the different CRs are made on their respective landscapes which only offer a partial image of the system, and at their own timescales. The system remains in equilibrium as long as the synchronism of the clocks allows that these choices be more or less coordinated (in this case, the duration of steps and delays in latency of different levels will be perfectly adjusted). But external or internal constraints can act more specifically on certain levels and thus render the choices of the CRs conflictual. This explains that the strategies chosen by the agents of a particular CR do not always succeed; in this case, its step will be terminated earlier than intended in the initial programming and there will be a fracture in its landscape, requiring a new strategy to regain homeostasis at this level.
This process is better understood if we consider the case of two CRs, one of a 'microlevel', whose agents are termed microagents, the other of a 'macrolevel'. Changes in the microlevel are too rapid to be transmitted in real time to the macrolevel; they are individually imperceptible for the macroagents and the system's global change appears to them to be continuous, smooth compared with the microevolution (that develops according to a discontinuous progression of microsteps). As long as the two CRs remain synchronized, the macrolevel can simply readjust the situation at the scheduled termination of its step. However, there is the danger that the moment will come when the constraints or microchanges will accumulate so rapidly during the progression of the macrostep that it will be interrupted following a total inadaptation of the strategy at this level, thus causing a fracture at this macrolevel.
For example, to again take the example used at the beginning of the paragraph, the macroagents impose the replication strategy to the microagents. For the microagents, the replication phase develops in several microsteps, each corresponding to a strategy of copy and verification of bases, or repair: what follows is a change in the landscapes by combination of pDNA with the base and molecules needed to replicate it, combination of SSB protein with the following bases, combination of simple repair enzymes with the DNA parts they will patrol...
In the case of very extended lesions of the bases, the simple repair system is overflowed, and there is no more strategy admissible for the microagents as the strict pairing of bases cannot be respected. The replication strategy imposed by the macrolevel is blocked and everything happens as if the macroagents measured the difference between the anticipated landscape and the effective landscape. What follows is a fracture at the macrolevel, with a change of macrostep, and adoption of a new strategy by the macroagents to permit the renewal of replication: derepression of the SOS system by the combination of DNA fragments linked to SSB with RecA (triple complex), whereby fission of the LexA protein that permits derepression of the SOS system whose activation allows to renew replication, eventually by accepting a mutation (Little & Mount 1982).
D/ Aging as a consequence of the dialectics between CRs
If the evolutive system has CRs which are heterogeneous with respect to their timescales and levels of complexity, a fracture in a landscape at a high level, say n+1, followed by a change in strategy and inauguration of a new step can have repercussions on the CRs at lower levels, in particular n, retroactively imposing a microfracture on them and secondarily a change in strategy. This corresponds to a dialectics between CRs, represented in the form of a loop of retroactions:
level n -----> level n+1 -----> level n.
But this dialectics requires a synchronism between the levels to maintain an equilibrium of the whole system. Aging will be caused by the progressive loss of this synchronism. To define it more precisely, we will need the following concepts (cf. Ehresmann & Vanbremeersch 1991).
1) Latency delays
a) Propagation delays of the links
The links represent informational messages or energy transfers (reception of information, for example the presence of an antigen, or command of effectors), whose transmission requires a certain latency delay, which is an internal structural constraint. Therefore, a propagation delay is associated with each link, which is a function of the levels of the linked components and the instant considered. It increases with the level of components. A simple chemical message is sent more rapidly than a humoral response requiring the synthesis of various products.
These delays are not to be defined precisely, only their order of magnitude is to be considered. In the first approximation, we associate an average propagation delay, written pn (or only p if no confusion is possible) for the links between the components of level n or between the levels n and n-1.
b) Problem of duration of a step
The duration of successive operations to develop a step constitutes a primary factor of internal constraint for the global evolution of the system.
We shall consider for each CR the average duration (determining its 'actual present'), called its period and written dn (or simply d ) for a CR of level n. This period represents the duration necessary to receive the messages that permit the formation of the landscape (p1), communication between agents to choose a strategy (p2), and to realize it (p3). This is therefore the latency time of the agents in the CR. Depending on the CR, this period will vary, the steps of a level being of a much shorter duration than those of the more complex levels; intuitively, it will take much less time to carry out a step at the molecular level (pair two bases), than a step at the cellular level (duplicate the cell, where d corresponds to the duration of a cell cycle). It is the duration of its actual present, thus its period, that determines the timescale proper to the CR. In the case of fracture at its level, the duration of the current step will be reduced.
2) Problems of synchronization
A first temporal constraint for a CR to function is that its period d be greater than 3p, where p is the average propagation delay of links between its agents and between these and the components of the lower level; otherwise there will not be time enough for development of the operations necessary for the completion of a step. This duration d should be far greater, as realizing the strategy takes more time than a simple transmission of information, and the CR risks having to eventually change this strategy in the case of an inadequate result. It would then be necessary to have
d >> p (where >> signifies 'of a greater magnitude order').
But the synchronism between levels also requires a certain compatibility between the propagation delays, the duration of the step, and the stability span during which is maintained the complex identity of the complex components intervening in the landscape of the CR (defined in §B). More precisely, the system can only function correctly if each CR satisfies the following inequalities:
called the temporal constraints for the CR.
Indeed, if the CR is at level n:
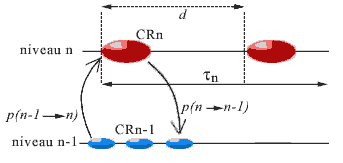
- the average stability span t maintaining the complex identity of the components of level n must be much greater than the propagation delays p of the links between these components or between them and those of the lower level, so that these components remain stable during an exchange between the levels (analysis of information, command of effectors);
- this average stability span t maintaining the complex identity must also be much greater than the period d of the CR, so that a complex object intervening in the strategy of CR is not denatured before the strategy is carried out (without which there would be a fracture interrupting the step because of the impossibility of pursuing this strategy).
Thus the inequalities characterizing synchronization permit that a message sent by one level (for example, the saturation of enzymes ensuring simple repairs during DNA replication) can receive a response from the higher level (triggering of SOS system) before the changes become catastrophic.
3) Consequence for aging
Aging will be defined as a progressive decrease of the average ratios t/d and t/p relative to different CRs. This decrease can result from a decrease of t (the components become denatured more rapidly) or from an extension of the propagation delays p (the communications slow down) and of the duration of the steps d (consequence of the propagation delays). In the section that follows we shall see that this hypothesis appears to unify the different physiological theories of aging that have been proposed, each referring to a different level.
The decrease of t/d and t/p must safeguard the temporal constraints for each CR, which can also be expressed by the inequalities:
The result is that such a decrease at a certain level will be propagated at higher levels; there is what we would term a progressive de/resynchronization of different levels. (Cf. Note)
We mention that the inequalities (1) must only be satisfied 'on the average', which signifies that, if one of these structural constraints is not respected at a certain instant for a CR, for example following a fracture, it will be rapidly compensated for (during the following step) by repair mechanisms controlled by the same CR or by other CRs. The pathology would correspond to the case where this compensation cannot be produced rapidly enough, that is, it is impossible for the organism to maintain its homeostasis, eventually leading to death. In normal senescence, the minimum threshold of 1 for t/d is continuously approached, on a more or less long duration, and the repairs are carried out more slowly.
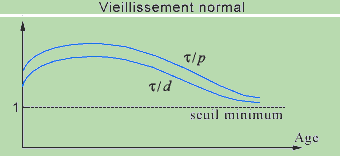
Graphically, this hypothesis leads to represent the curves of t/d and t/p as a function of time under the following form, where the descending part corresponds to aging. The intensity of this decrease measures the more or less great rapidity with which the organism ages. The 'rising' part of the curves would correspond to the growth phase that presents a rapid rhythm of structural transformations, with a t initially low, which will gradually decreases, the delays p remaining relatively stable.
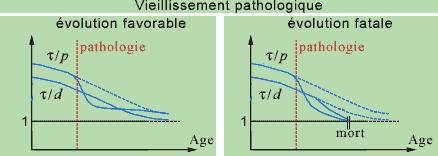
The pathology would then correspond to the case where the slope of t/p relative to some CR of higher or lower levels presents a sudden change in direction that makes its curve pass under that of t/d, even though the latter also decreases. Depending to the intensity of this change in direction, it will be possible to recover the initial position after repair, or the slope of t/d will also decrease suddenly, so that it will go beyond the minimum threshold; this would correspond to the case where it is impossible for the system to recover its equilibrium, and thus death.
Another consequence of the analysis of these relations would be the realization of the quasi-absence of aging in a certain number of cases. If a system has a restricted number of hierarchical levels, thus a weak complexity, with, in addition, few external functional relations, permitting such an adaptation that the relation t/d remains almost invariable, it will undergo little aging, except if the external constraints become too great. That could be the case of cancer cells and certain isolated cells such as spermatogonia.
II. INTERPRETATION IN THE MODEL OF DIFFERENT PHYSIOLOGICAL THEORIES OF AGING
Several physiological theories have been proposed that attribute aging to phenomena at the molecular or cellular levels. These theories are interpreted in the proposed model, as we are going to demonstrate, by an accelerated decrease of the complex identity of some components or by the extension of communication delays between levels, thus desynchronization of different cycles, leading to fractures at higher and higher levels. They will therefore justify, experimentally, the thesis proposed in the preceding section, specifically that aging results from a progressive desynchronization of different levels, with a decrease in ratios of the stability span t of the components on one hand to the propagation delays p, on the other hand to the period d of steps relative to a CR.
A/ Macromolecular level
Most authors base the phenomena of aging at this level.
1) Decrease in stability of components
It is recognized that with age, the complex identity of proteins and DNA is less well maintained (t decreases at the macromolecular level), following an accelerated DNA mutation rate (Sinex 1977) and a more rapid degradation of proteins with an accumulation of defective enzymes (having lost 30 to 70% of their catalytic activity, Gershon 1979).
a) Instability of proteins
Orgel's theory (1963) attributes cell aging to a poor translation of mRNA that produces defective proteins by incorrect substitution of amino acids. This would result in a "catastrophe of errors", following poor enzyme functioning. (In our model, this would be expressed by a poor performance of strategies selected by the RNAs, which will reflect back to the other levels.) Since then contradictory results have been obtained. Thermolabile enzymes were detected in fibroblasts (Holliday et al. 1981, Goldstein & Moerman 1976), in particular in the course of diseases imitating accelerated aging (Progeria, Werner's syndrome, Goldstein 1978). But other experiments did not corroborate the hypothesis of a routine increase in errors of protein synthesis with age (Harley & Goldstein 1980, Wojtyk & Goldstein 1980).
Strehler's theory (Strehler et al. 1971) supposes a fracture in the functioning of certain tRNAs, so that the code degenerates and the rapid translation of messages cannot be carried out.
b) Instability of the genome
More frequent DNA mutations were implicated by various authors as the basis of aging. Errors could be stochastic (Szilard 1959, Burnet 1982, Holliday et al. 1981), or result from an "aging program" (Sinex 1977). They could also be due to a defect in the mechanisms of DNA repair, although there is no evidence that these are modified with age (Goldstein 1978, Gensler 1981).
Chronogenetics (Gedda & Brenci 1975) attributes senescence to a progressive and differentiated exhaustion of the stability span and of the intensity of action of genes (measured by their "chronon" and "ergon" that are proportional to the t of the gene and its products).
Other causes of genome instability altering its functional duration (thus decrease in its t) have been implicated in aging. Thus a dysdifferentiation of certain genes that lose their specificity would result in a decrease in DNA methylation to specific regions close to the gene (theory of Cutler 1985, Holliday 1987). A similar cause would be at the basis of the reactivation of the inactivated X-chromosome (Holliday 1992).
Repeated DNA sequences may facilitate the formation of extrachromosomal circular DNA molecules (Shrnookler et al. 1986), which would increase the genome's instability (thus would decrease its t). Thus the DNA functioning (in Podospora) is disturbed by one of the introns of mitochondrial DNA encoding for chytochrome-oxidase, a plasmid that would be reinserted into the DNA and block gene expression (cf. Esser 1985).
2) Extension of functioning delays
Insufficient maintenance of the complex identity for DNA, RNA and proteins (decrease of t, see above) results in a lowering of their activity and, consequently, an increase in the delays of latency and propagation p and in the duration d of the steps at the macromolecular level. This results in a desynchronization of the molecular, macromolecular and cellular levels, leading to fractures that are more and more difficult to overcome.
The renewal of proteins lowers with age and abnormal proteins are maintained, for example in the mouse liver (Lavie et al. 1982). It appears that protein degradation results from inadequate elongation rather than a defect in the initiation of the synthesis (cf. Danner et al. 1990, Webster 1985). Thus, a reduction of 20 to 25% of catalytic activity of the elongation factor EF10a has been observed, and could result from post-translational modifications (Rattan et al. 1986).
RNA synthesis also decreases (cf. Danner & Holbrook 1990), especially the mRNA (80-90% decline, Richardson & Semsel 1987), the maturation of which could be altered.
B/ Level of infracellular structures
Here the changes are essentially due to a slowing down of intralevel communications and communications with the lower level, that is, a lengthening of p. Combined with the decrease of t at the macromolecular level (cf. above), it results in a desynchronization between these levels that is amplified over time, resulting in deteriorations by reciprocal fractures of different components (decrease in their t).
1) Degradation of mitochondria
In the mitochondria, aging is manifested at the microlevel by a poor functioning of the ion transport system and a loss of their capacity to carry out the Krebs cycle generating ATP (Robert 1990); this results in an increase of p. It leads to membrane fatigue (due to poor control of Ca++ and Mg++ ions) and an increase in the proportion of incompletely reduced oxygen (2% in normal times) that appears in the form of free radicals (cf. LeBel & Bondy 1992, Pacifici & Davies 1991).
2) Theories implicating free radicals
Numerous authors have implicated free radicals as responsible for aging (cf. Laborit 1987, Harman 1986). They are one of the factors intervening in most of the cell deterioration mentioned above, and the defense system capable of neutralizing them (superoxide dismutase, glutathion peroxidase, vitamin E...) may decrease with age (Pacifici & Davies 1990).
In different types of cells, the accumulation of free radicals results in membrane degradation (thus, a decrease in their t). Consequently, in erythrocytes and the brain, they attack the protein Band3, which is one of the principal constituents of membranes both from the structural and functional viewpoint. One of the products of this protein alteration is termed "aging cell antigen", as it binds an auto-antibody IgG, which marks the cell for death (Bartosz 1991, Kay 1991).
The degradation of membrane lipids by free radicals also results in the accumulation of lipoprotein particles, or lipofuscin, (up to 6 to 7% of the intracellular volume at 90 years of age), in particular in the myocardium and central nervous system, with a slowing down of the renewal of organelles, such as mitochondria (Robert 1983).
3) Changes in the cytoskeleton
Macieira-Coelho et al. (1986) implicate another harmful loop, this time between the macromolecules and the cytoskeleton: a reorganization of the genes of the cytoskeleton results in modifications of the links between membranes and the nucleus (thus a lengthening of p for the organelles), and thus a poor anchoring of the DNA and a slowing down of intracellular communications, which increases the duration of the cell cycle (considered below) by delaying its initiation.
C/ Cellular level
All the changes at the lower levels have repercussions at this level by increasing its p and d. The lengthening of the cell cycle (thus of d ) can result in a longer latency phase G0 (Bazerga 1977, Hayflick 1977), or a slower DNA replication. Dysfunctions of the cycle time produce messages that are poorly transmitted to the chromatin, and the cells will divide before DNA doubling, resulting in a loss of volume (for the ciliates, cf. Smith et al. 1990).
For numerous types of cells, a clear decrease in the number of replications was observed with age (loss of 0.2 duplications per year of age for normal human fibroblasts, Martin et al. 1970); this led to the idea that cellular aging would be encoded in the genome by an appropriate clock and that the number of duplications of cells in continuous mitosis would be limited (model of Hayflick 1977; cf. Robert 1983, 1990).
In the immune system, a larger number of aged T-lymphocytes do not enter into mitosis in the presence of activators, perhaps subsequent to defects in Ca++ signals (Miller 1990) or as a consequence of a lesser density of IL-2 receptors (cf. Bums & Goodwin 1991), in contrast, the changes are less marked for B-lymphocytes, antigen-presenting cells and neutrophils, at least in the healthy aged subject (Kennes et al. 1986, Coberand et al. 1986).
At present, it is not known if cell death is a programmed phenomenon external or internal to the cell ("death genes"), or if it intervenes in a stochastic manner (cf. Raff 1992).
D/ Higher levels (tissues, organs, large systems)
Here the phenomena are the consequence of modifications of lower levels. The decrease of their s and lengthening of their p and d are combined to deteriorate the interlevel communications by increasing the propagation delays (thus p) at the tissue level and cause subsequent fractures at different levels, resulting in more or less considerable changes whether aging is associated with disease or not.
1) Degradation of the extracellular matrix
Several authors (cf. Robert 1983, 1990) emphasize the changes in the composition of the extracellular matrix (thus, t decreases) during aging. The bypass theory of Verzar (1957) is based on the increase of intercatenary bonds (bypasses) of collagen, in part due to free radicals (Rigby et al. 1977). The elastin/glycoprotein ratio of the structure in the aorta routinely decreases with age (Moschetto et al. 1974). The thickness of the basement membranes increases (A.M. Robert et al. 1977). Generally, the degradation of the matrix would result (Robert 1990) from the interaction between the deterministic mechanism (encoding the informational loop between the matrix and the cell which develops it) and stochastic events (UV radiation, nutritional factors). The result is the deterioration of tissues rich in matrix.
Thus, the vitreous body, composed especially of collagen fibrils and hyaluronic acid, progressively liquefies (Robert 1983). In the normal lens, the SOD activity decreases with age (Ohrloff & Hockwin 1986), as does the membrane potential, while the total concentration of sodium increases (Duncan & Hightower 1986). These changes are more pronounced in the case of cataracts.
The bone, which is made up of more than 80% collagen, undergoes a decrease in its density due to an increase in catabolism of the calcifiable matrix; this results in osteoporosis, in particular in women after menopause, or over the age of 70 (Riggs & Melton 1986).
The water content decreases while the collagen content increases with an increase in bypass (Meynadier 1980). The speed of cicatrization decreases exponentially with age (Lecomte de Noüy 1936).
2) Slowing down of communications
Less effective exchanges between cells and tissues (lengthening of p) by hormones or neuromediators result in a functional decrease of metabolic regulation in response to external or internal stimuli; there will be an increase in the latency period of induction (thus p of tissues) and a decrease in the amplitude of the responses of effectors (Adelman 1979). The result is that homeostasis is more difficult to reestablish at the level of the large systems (longer duration d of step).
For example, nerve conductivity decreases 15% between the ages of 30 and 90, the cardiac index at rest decreases 30%, renal circulation 50% around 50 years of age, while the maximal respiratory capacity decreases 60 to 70%; the muscle strength decreases markedly only around the age of 65-70 (Robert 1983). These changes are greater in the case of diseases, such as arteriosclerosis, which occurs frequently. The adreno-cortical axis becomes more vulnerable in the case of stress, with a tendency towards excessive secretion of glucocorticoids, which conversely can accelerate aging and give rise to diseases (Sapolsky 1990).
We shall not discuss aging of the immune system, which we have already mentioned several times.
3) Aging of the nervous system
In the nervous system, the weight of the brain decreases 2% per decade over the age of 50, with glial atrophy and dilatation of the ventricles (Horvath & Davis 1990), the loss of white matter becoming preponderant over the age of 50 (Miller et al. 1980). The multisynaptic transmissions slow down following an insufficient renewal of neuromediators, especially catecholaminergic; but the GABA-ergic system does not appear to vary (Robert 1983). Contradictory results were obtained concerning the role of free radicals in all the cerebral changes (LeBel & Bondy 1992, Aston-Jones 1985). Senile plaques with amyloid substance between the neurons (especially in levels II and III of the cortico-cortical connections, Duyckaerts et al. 1987), and cerebral vascular amylosis (infiltration of cerebral vessel walls by amyloid substance) can be found in the normal aging brain (Hauw et al. 1987) although they are more developed in the case of dementias, in particular Alzheimer disease, where they are associated with neurofibrillar degeneration with the presence of abnormal filaments that can fill the neuron (Lamour 1991).
From the cognitive viewpoint, in normal aging (in contrast to the pathological case), it is essentially the central processes such as attention that would be affected, and their functional rapidity decreases (Signoret 1987). There can be progressive deterioration of the frontal system, in particular in the right hemispheres, less good perceptuo-motor integration, and language and memory disorders, although these are not as severe as usually believed (Albert 1987). The rhythm a is slowed down (Robert 1983).
4) Slowing down of biological rhythms
Generally, biological rhythm disorders have been detected. The circadian cycle lengthens and the amplitude of the circadian variations of some endocrine variables decreases (consequently a lengthening of delays p at different levels), but the effects of these changes are difficult to evaluate (Richardson 1990). For Robert (1989), there is a hierarchy of biological clocks (perhaps even one in each cell), up to a "master clock" at the level of the hypothalamus (we return to the pineal gland of Descartes!) synchronizing the others through hormone synthesis. The decrease in the number of cell divisions (cf. above) will modify gene expression of these hormones, consequently a progressive disorder of the ensemble.
E/ Global phenomena
More theoretical studies have suggested that aging would not be due to local errors (such as accelerated degradation of proteins), but would be inherent to the global organization of a complex system. Thus, Rosen (1978) showed that any system that, like an organism, has feedforward loops can show global modes of failure; the different subsystems function correctly as far as can be judged according to local criteria, but each loop has only a limited lifetime, so that the system in its ensemble becomes less and less adapted in the course of time: "It is possible for a complex system to exhibit global modes of failure which are not associated with local subsystem failures. It is a priori conceivable that senescence is associated with such non-localized or global modes of failure" (Rosen 1978, p. 580).
Other authors (Baas 1975, Sutton et al. 1988) have also implicated the hierarchical organization of the organism in the phenomenon of aging. Laborit (1987) also considers the intervention of the socioeconomic level: he thinks that the inhibition of the gratifying action would be one of the factors accelerating the aging process (which he believes is genetically programmed).
CONCLUSION
Our theory of aging by a "cascade of de/resynchronizations" is related to these recent studies. It allows to refine them in our categorical model for complex systems, taking into account the dialectics between the different CRs of the organism. Furthermore, as we showed in the preceding pages, it offers a framework for a synthesis unifying different physiological theories of a more local nature, and appears to encompass a large number of biological results. Let us remember that it is based essentially on the properties of an evolutive hierarchical system in which the dynamics is modulated by the dialectics between a net of CRs which are heterogeneous by their level of complexity and their timescale.
Even if we suppose that each CR acts in a deterministic manner and has good repair systems, these risk being submerged at times under the effects of stochastic external disturbances. The fracture thus caused at one level will affect higher CRs that might intervene to reduce it, with the risk of destabilizing certain components by modifying their complex identity (consider the SOS system in bacteria that will make a mutation acceptable). In the long run, these changes make the loops of interactions between CRs perform less, so that the information and responses will arrive with greater and greater delays resulting in a more pronounced desynchronization between the levels. Consequently, there is an increasing difficulty in reestablishing an equilibrium of the global system, as the errors to be corrected become more numerous. This process of destabilization by progressive desynchronization characterizes aging and terminates in death, either by total paralysis of the system ('normal' physiological aging), or by uncontrolled rupture of a subsystem (pathological case). Thus, aging would result in an innate/acquired dialectics between:
- the determinist limitation of local repair systems, of informational loops permitting interlevel synchronization, perhaps also of the number of cellular duplications ("death genes");
- the influence of stochastic external disturbances.
In this scheme, the correction of errors at one level, when they are too numerous, requires the intervention of a higher level. A given CR can act against errors for which it is programmed, but it can only perceive the saturation of its repair mechanisms in a negative manner (fracture), when its functioning is stopped: only from the outside and with a certain latency period can this saturation be 'understood' (Ehresmann & Vanbremeersch [1990] demonstrated that in an evolutive system with memory, the 'meaning' of a situation or of a fracture can only be perceived at a higher level), and therefore eventually remedied by imposing a radical change in strategy which alters the equilibrium between these levels. But then the same phenomenon occurs at higher and higher levels so that there comes a time when there is no longer any recourse within the system.
The organism has only two strategies to fight against this: to decrease the external risks so that its repair mechanisms are not pushed to the limit by the unexpected, that is, to restrict itself to an environment that is not too disturbing; or to develop repair systems at higher and higher levels, thus becoming more complex. These two strategies were used by natural selection: either by specializing species in very particular niches, or by making complex organisms, that also has its limits. According to Burnet (1982), natural selection could not combat aging as it does not have the means of action on the individual beyond the period of reproduction (which leaves open the question: why does the reproduction period stop for women, and does so relatively early?). Another response, which is suggested by the preceding considerations, would be that natural selection does not act on the individual level but only on that of the species, and that death of the individual would be its way of correcting, at the higher level of the species, the errors that led to aging. No doubt this response would not be to the liking of those who wish to prolong life more and more.
REFERENCES
Adelman, R,C. (1979); Loss of adaptive mechanisms during aging; Fed. Proc. 38, 1968-1971.
Albert, M.L. (1987); Caractéristiques cliniques du vieillissement cérébral normal; in Le vieillissement cérébral normal et pathologique, Maloine, 22-28.
ASSIM (1991); Immunologie Générale, 2e édition; MEDSI/McGraw-Hill.
Aston-Jones, G., Rogers, J., Shaver, R-D-, Dinan, T.G. & Mass, D.E. (1985); Age-impaired impulse flow from nucleus basalis to cortex; Nature 318, 462-465.
Baas, N.A. (1976); Hierarchical Systems. Foundations of a mathematical theory and applications; Report Mathematics 2/76, Mate. Inst,, Univ. Trondheim.
Bartosz, G. (1991); Erythrocyte aging: physical and chemical membrane changes; Gerontology 37 n° 1-3, 33-67.
Bazerga, R.L. (1977); Cell division and the cell cycle; in Handbook of the biology of aging, vol. 1 (Finch & Hayflick, ed.); Von Nostrand, 101-121.
Burnet MacFarlane (1982); Le programme et l'erreur; Albin Michel.
Burns, E.A. & Goodwin, J.S. (1991); Immunologie et vieillissement. Travaux récents; in L'Année Gérontologique (Albarède & Vellas, ed.); Serdi, Paris, 19-29.
Corberand, J.X., Laharrague, P.F. & Fillola, G. (1986); Polymorphonuclear functions in healthy aged humans selected according to the Senior protocol recommendations; in Modern trends in aging research, Coll. INSERM-EURAGE, John Libbey Eurotex LTD, vol. 147, 235-241.
Cutler, R. G (1985); Antioxydants and longevity of mammalian species; Basic Life Sciences 35, 15-73.
Danner, D.B. & Holbrook, N.J. (1990); Alterations in gene expression with aging; in Handbook of the biology of aging, 3rd edition; Acad. Press. 97-115.
Duncan, G. & Hightower, K.R. (1986); Age-related changes in human lens membrane physiology; in Modern trends in aging research; Coll. INSERM-EURAGE, John Libbey Eurotex LTD, vol. 147, 341-348.
Duyckaerts, C., Delaere, P., Brion, J.-P., Fiente, F. & Hauw, J.-J. (1987); Les plaques séniles; in Le vieillissement cérébral normal et pathologique; Maloine, 157-163.
Ehresmann, A,C. & Vanbremeersch, J.-P. (1987); Hierarchical evolutive systems: a mathematical model for complex systems; Bull. Math. Biology, 49 N°1, 13-50.
- (1989); Modèle d'interaction dynamique entre un système complexe et des agents; Revue Intern. Systémique 3, 315-341.
- (1990); Hierarchical evolutive systems; in Conf. Proc. 8th Intern. Congress of Cybernetics and Systems (New York, 1990; ed. Manikopoulos), 320-327.
- (1991); Un modèle pour des systèmes évolutifs avec mémoire, basé sur la Théorie des catégories; Revue Intern. Systémique 5 N°1, 5-25.
- (1992); Outils mathématiques utilisés pour modéliser les systèmes complexes; Cahiers de Top. et Géom. Diff. Catég. XXXIII-3.
Esser, K. (1985); Genetic control of aging: The mobile intron model; in The thresholds of aging (Bergener, Ermini & Stahelin, ed.); Academic Press, 4-20.
Gedda, L.C. & Brenci, G. (1975); Chronogénétique: l'hérédité du temps biologique; Hermann, Paris.
Gensler, H.L. (1981); The effect of hamster age in UV-induced unscheduled DNA synthesis in freshly isolated lung and kidney cells; Exper. Gerontology 16, 59-68.
Gershon, H.L. (1979); Current status of age altered enzymes: altemative mechanisms; Mech. Aging Develop. 9, 189-196.
Goldstein, S. (1978); Human genetic disorders which feature accelerated aging; in The genetics of aging (ed. Schneider); Plenum, 171-224.
Goldstein, S. & Moerman, E.J. (1976); Defective proteins in normal and abnormal human fibroblasts during aging in vitro; in Cellular ageing: concepts and mechanisms, Part 1 (ed. Cutler); S. Karger, 24-43.
Harley, C.B. & Goldstein, S. l1980); Retesting the commitment theory of cellular aging; Science 207, 191-193.
Harman, D. (1986), Free radical theory of aging: role of free radical reactions in the origination and evolution of life, aging and disease processes; in Modern trends in aging research; Coll. INSERM-EURAGE, John Libbey Eurotex LTD, vol. 147, 77-83.
Hastie, N.D., Dempster, M., Dunlop, M.G., Thompson, A.M., Green, D.K. & Allshire, R.C. (1990); Telomere reduction in human colorectal carcinoma and with ageing; Nature 346, 866-868.
Hauw, J.-J., Delaere, P. & Duyckaerts, C. (1987); La sénescence cérébrale: données morphologiques; in Le vieillissement cérébral normal et pathologique; Maloine, 139-156.
Hayflick, L. (1977); The cellular basis for biological aging; in Handbook of the biology of aging (ed. Finch, C.E. & Hayflick, L.); van Nostrand-Reinhold.
Holliday, R. (1987); The inheritance of epigenetic defects; Science 238, 163-170.
Holliday, R. (1987); X-chromosome reactivation; Nature 327, 663.
Holliday, R., Huschtscha, L.l. & Kirkwood, T.B.L. (1981); Cellular aging: further evidence for the commitment theory; Science 213, 1505-l507.
Horvath, T.B. & Davis, K.L. (1990); Central nervous system disorders in aging; in Handbook of the biology of aging (ed. Schneider & Rowe); van Nostrand, 307-329.
Kay, M.M.B. (1991); Drosophila to bacteriophage to erythrocyte: the erythrocyte as a model for molecular and membrane aging of terminally differentiated cells; Gerontology. 37, n° 1-3, 5-32.
Kennes, B.J., Devière, J., Brohée, D., de Maertelaer, V. & Neve, P. (1986); The effect of age, sex and health status on the distribution and functions of human blood mononuclear subpopulations; in Modern trends in aging research; Coll. INSERM-EURAGE, John Libbey Eurotex LTD, Vol. 147, 231-234.
Laborit, H. (1987): Comportement et vieillissement; in Le vieillissement cérébral normal et pathologique; Maloine, 44-60.
Lamour, Y. (1991); Démences de type Alzheimer: de l'anomalie génétique à la lésion structurale; La Revue de Gériatrie, Supplément au n° 3, 15-28.
Lavie, G., Reznick, A.Z. & Gershon, D. (1982); Decreased proteins and puromycinyl peptide degradation in livers of senescent mice; Biochem. J. 202, 47-51.
LeBel, C.P. & Bondy, S.C. (1992); Oxidative damage and cerebral aging; Progress in Neurobiology 38, 601-609.
Lecomte de Noüy, P. (1936); Le temps et la vie; Gallimard, Paris.
Little, J.W. & Mount, D.W. (1982); The SOS regulatory system of E. coli; Cell 29, 11-22.
Macieira-Coelho, A., Liepkalns, C.I., Puvion-Dutilleul, F. (1986); Genome reorganization during senescence of dividing cells; Modern trends in aging research; Coll. INSERM-EURAGE, John Libbey Eurotex LTD, Vol. 147, 41-54.
MacLane, S. (1971); Categories for the working mathematician; Springer.
Martin, G.M., Sprague, C.A. & Epstein, C.J. (1970); Replicative life span of cultivated human cells. Effect of donor's age, tissue and genotype; Lab. Invest. 23, 86-92.
Meynadier, J. (1980): Précis de physiologie cutanée; La Porte Verte, Paris.
Miller, A.K.H., Alston, R.L. & Corsellis, J.A.N. (1980); Variation with age in the volumes of grey and white matter in the cerebral hemispheres of man; measurements with an image analyser; Neuropath. Appl. Neurobiol. 6, 119-132.
Miller, R.A. (1990); Aging and the immune response, in Handbook of the biology of aging, 3rd edition; Acad. Press,157-180.
Moschetto, Y., De Backer, M., Pizieu, O., Bouissou, H., Pieraggi, M.T. & Rufian, M. (1974); Evolution de l'élastine d'aortes humaines au cours du vieillissement; Paroi artérielle 2, 161-177.
Ohrloff, C. & Hockwin, O. (1986); Superoxide dismutase (SOD) in normal and cataractous human lenses: in Modern trends in aging research; Coll. INSERM-EURAGE, John Libbey Eurotex LTD, Vol. 147, 365-371.
Orgel, L.E. (1963); The maintenance of the accuracy of protein synthesis and its relevance to aging; Proc. Natl. Acad. Sci 49, 517.
- (1970); The maintenance of the accuracy of protein synthesis and its relevance to aging; correction; Proc. Natl. Acad. Sci. 67, 1476.
Pacifici, R.E. & Davies, K.J.A. (1991); Protein, lipid and DNA repair systems in oxidative stress: the free-radical theory of aging revisited; Gerontology 37/1, 166-180.
Radman, M. (1975); SOS repair hypothesis: phenomenology of an inducible DNA repair which is accompanied by mutagenesis; in Molecular mechanisms for repair of DNA (ed. Hanawalt & Setlow); Plenum Press 355-367.
Raff, M. C. (1992); Social controls on cell survival and cell death; Nature 356, 397-399.
Rattan, S.I.S., Cavallius, J., Hartvigsen, G.K. & Clark, B.F.C. (1986); Amounts of active elongation factor 1a and its activity in livers of mice during aging; in Modern trends in aging research; Coll. INSERM-EURAGE, John Libbey Eurotex LTD, Vol. 147, 135-139.
Richardson, G.S. (1990); Circadian rythms and aging; in Handbook of the biology of aging, 3rd edition; Acad. Press.
Richardson, A. & Semsei, I. (1987); Effect of aging on translation and transcription; Review of biological research in aging 3, 467-483.
Rigby, B.J., Mitchell, T.W. & Robinson, M.S. (1977); Oxygen participation in the in vivo and in vitro aging of collagen fibers; Biochem. Biophys. Res. Com. 79, 400-405.
Riggs, B.L. & Melton, L.J. (1986); Involutional osteoporosis; New England Journal of Medecine 314, 1676-1696.
Robert, A.M., Boniface, R. & Robert, L. (1977); Biochemistry and pathology of basement membranes; in Frontiers of matrix biology, Vol. 7; Karger.
Robert, L. (1983); Mécanismes cellulaires et moléculaires du vieillissement; Masson, Paris.
- (1989); Les horloges biologiques; Flammarion, Paris.
- (1990); Théories du vieillissement biologique; in Interdisciplinarité en Gérontologie (ed. R. Hebert); Maloine, Paris.
Rosen, R. (1978); Feedforwards and global system failure: a general mechanism for senescence; J.Theor. Biol. 74, 579-590.
Signoret, J.-L. (1987); Le vieillissement du cerveau est-il modulaire?; in Le vieillissement cérébral normal et pathologique; Maloine, 61-72.
Sapolsky, R.M. (1990); The adrenocortical axis; in Handbook of trie biology of aging (ed. Schneider & Rowe); Van Nostrand, 330-346.
Shmookler, R.J., Riabowol, K.T., Jones, R.A., Ravishanker, S. & Goldstein, S. (1986); Extrasomal circular DNAs from senescent human fibroblasts contain an over-representation of Alu1 and Kpn1 interspersed repeats, which may reflect genetic instability; in Modern trends in aging research; Coll. INSERM-EURAGE, John Libbey Eurotex LTD, Vol. 147, 31-39.
Sinex, F.M. (1977); The molecular genetics of aging; in Handbook of the biology of aging (ed. Finch & Hayflick); Van Nostrand, 639-665.
Smith-Sonneborn, J. (1990); Aging in Protozoa; in Handbook of the biology of aging (ed. Schneider & Rowe); Van Nostrand, 24-44.
Springer, T.A. (1990); Adhesion receptors of the immune system; Nature 346, 425-434.
Strehler. B.L., Hirsch, G., Gussek, D., Johnson, A.S. & Bick, M. (1971): Codon restriction theory of aging and development; J. Theoret. Biol. 33, 429-474.
Sutton, J.P., Beis, J.S. & Trainor, L.E.H. (1988); A hierarchical model of neocortical synaptic organization; Mathl. Comput. Modelling 11, 346-350.
Sutton, J.P., Beis, J.S. & Trainor, L.E. H. (1988); Hierarchical model of memory and memory loss; J. Phys. A: Math. Gen. 21, 4443-4454.
Szilard, L, (19S9); On the nature of the aging process; Proc. Natl. Acad. Sci. of the U.S.A. 45, 30-45.
Verzar, F. (1957), Aging of connective tissue; Gerontol. 1, 363-378.
Webster, G.C. (1985); Protein synthesis in aging organisms; in Molecular biology of aging: gene stability and gene expression (ed. Sohal, Birnbaum & Cutler); Raven Press.
Wojtyk, R.I. & Goldstein, S. (1980); Fidelity of protein synthesis does not decline during aging of cultured human fibroblasts; J. Cell Physiol. 103, 299-303.
|
Note: |
|
Whence made smooth, the period d of the CR can be interpreted as the period of an oscillating process for a limit cycle in a dissipative system with multiple regulations (Prigogine); then the changes of t and p correspond to a change of initial conditions that might lead to a brief chaotic state, before coming back to an oscillating process for another limit cycle whose period would be that of the CR after desynchronization. (Return) |






