|
|
|
|
|
|
|
|
|
To go directly a particular section of this paper, click on a section title below.
| 1. Howard's Delimma |
| 2. Principles of Deliberative Coherence |
| 3. Computational Implementation |
| 4. Comparison with Classical Decision Theory |
| 5. Conclusion: Goals and Learning |
In their introduction to this volume, Ram and Leake usefully distinguish between task goals and learning goals. Task goals are desired results or states in an external world, while learning goals are desired mental states that a learner seeks to acquire as part of the accomplishment of task goals. We agree with the fundamental claim that learning is an active and strategic process that takes place in the context of tasks and goals (see also Holland, Holyoak, Nisbett, and Thagard, 1986). But there are important questions about the nature of goals that have rarely been addressed. First, how can a cognitive system deal with incompatible task goals? Someone may want both to get lots of research done and to relax and have fun with his or her friends. Learning how to accomplish both these tasks will take place in the context of goals that cannot be fully realized together. Second, how are goals chosen in the first place and why are some goals judged to be more important than others? People do not simply come equipped with goals and priorities: we sometimes have to learn what is important to us by adjusting the importance of goals in the context of other compatible and incompatible goals. This paper presents a theory and a computational model of how goals can be adopted or rejected in the context of decision making. In contrast to classical decision theory, it views decision making as a process not only of choosing actions but also of evaluating goals. Our theory can therefore be construed as concerned with the goal-directed learning of goals.
"What's the matter, Howard?" asked the philosopher.
Replied the decision theorist: "It's horrible, Ernest - I've got an offer from Harvard and I don't know whether to accept it. "
"Why Howard, " reacted the philosopher, "you're one of the world's great experts on decision making. Why don't you just work out the decision tree, calculate the probabilities and expected outcomes, and determine which choice maximizes your expected utility?"
With annoyance, the other replied: "Come on, Ernest. This is serious."
In recent years, it has become increasingly clear that classical decision theory as devised by such theorists as von Neumann, Morgenstern, and Savage is inadequate both as a descriptive and as a normative theory of decision making. The main assault on its descriptive adequacy has come from Kahneman, Tversky and other experimental psychologists who have shown that the basic assumptions of decision theory, for example that preferences are transitive, are often violated by humans (Kahneman & Tversky, 1979; Tversky & Kahneman, 1981) . Nevertheless, decision theory remains a cornerstone of economic theorizing (Hausman, 1992; Kreps, 1990) . The intransigence of economists and other devotees of traditional decision theory would be puzzling but for the insight from history and philosophy of science that a theory is rarely abandoned just because it faces empirical difficulties; rejection of the problematic theory comes only when a new theory comes along that is visibly superior in that it can explain most of what the previous theory did and more. No theory of decision making with the precision and broad application of the classical theory has yet emerged.
We want to propose an account of the nature of human decision making that we think is more psychologically realistic than classical decision theory. In brief, decision making is inference to the best plan. When people make decisions, they do not simply choose an action to perform, but rather adopt complex plans on the basis of a holistic assessment of various competing actions and goals. Choosing a plan is in part a matter of evaluating goals as well as actions. Choice is made by arriving at a plan or plans that involves actions and goals that are coherent with other actions and goals to which one is committed. We will put forward a set of principles of coherence that govern the relations among actions and goals, and show how decisions can arise from these relations. Moreover, we show how coherence can be efficiently computed by connectionist algorithms for parallel constraint satisfaction.
Our set of principles and our computational implementation are in part derived analogically from a theory and computational model of explanatory coherence that has been applied to many cases of inference involving hypotheses . Just as theory evaluation can be viewed as inference to the best explanation, with the acceptability of hypotheses determined by a judgment of explanatory coherence, so decision making can be viewed as inference to the best plan, with the desirability of actions and goals determined by a judgment of what we call deliberative coherence.
We now propose a set of principles designed to specify the kinds of relations that exist among actions and goals and that give rise to coherence estimations that determine not only choices of actions to perform but also adoption of complex plans and revisions of goals. We make no sharp distinction between actions and goals, since what in one context is best described as an action may be best described in another context as a goal. For example, if my main goal is to travel from Waterloo to Princeton, I will set myself the subgoal of getting to Toronto airport, but this subgoal is itself an action to be performed. We will refer to actions and goals as factors in decision making. Factors are actions and goals that cohere with each other according to the following six principles.
1. Symmetry. Coherence and incoherence are symmetrical relations: If a factor (action or goal) F1 coheres with a factor F2, then F2 coheres with F1.
2. Facilitation. Consider actions A1 ... An that together facilitate the accomplishment of goal G. Then
(a) each Ai coheres with G,3 . Incompatibility.(b) each Ai coheres with each other Aj, and
(c) the greater the number of actions required, the less the coherence among actions and goals.
(a) If two factors cannot both be performed or achieved, then they are strongly incoherent.4. Goal priority. Some goals are desirable for intrinsic or other non-coherence reasons.(b) If two factors are difficult to perform or achieve together, then they are weakly incoherent.
5. Judgment. Facilitation and competition relations can depend on coherence with judgments about the acceptability of factual beliefs.
6. Decision. Decisions are made on the basis of an assessment of the overall coherence of a set of actions and goals.
As so far stated, these principles are rather vague and abstract. We can eliminate some of the abstraction by indicating how they apply in real cases, and some of the vagueness will be diminished when we show how coherence and the best plans can be computed. We are postulating that the cognitive structure of decision makers includes representations of actions and goals along with knowledge about what actions can be used to accomplish what goals. But the structure is much more complicated than just a set of actions each of which may or may not facilitate a set of goals. A plan is a set of factors that includes actions and goals. One of Howard's goals might be to further the scientific understanding of decision making. He might consider that a good way to do so would be to start a new institute for studying decision making, and perhaps moving to the new job would make possible such an institute. Then the action of taking the new job facilitates establishing the institute which facilitates the scientific understanding. Establishing the institute can be described equally well as an action to be taken and as a subgoal to the basic goal of increasing understanding. Thus principle 2, Facilitation, covers relations of coherence between subgoals and supergoals as well relations between actions and goals. Principle 1, Symmetry, notes that coherence, unlike facilitation, is a symmetrical relation. We will see, however, that the principle of goal priority introduces an important asymmetry in how coherence is actually calculated.
We assume that humans can represent many layers of actions, subgoals, and supergoals, as in the structure:
increase scientific understanding
<-- hire talented researchersUnlike a typical decision tree, however, Principle 2 bundles actions A1 ... An together in packages. This reflects how real world preconditions actually work. Typically, a number of actions will together be jointly necessary for the accomplishment of a goal or subgoal. For a new institute to facilitate scientific understanding, not only its establishment will be required: finding funding for it and office space will need to be done simultaneously. So the actual facilitation relation will be something like:<-- start institute<-- take job
increase scientific understanding
<-- hire talented researchers & encourage themPrinciple 2(c), according to which coherence decreases as more actions are required, is intended to encourage simpler plans. Principle 2(b) asserts that actions cohere with each other as well as with the goal they facilitate.<-- start institute & fund it & house it<-- take job
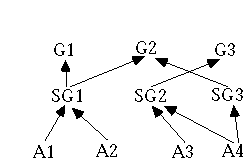
Figure 1 shows the sort of facilitation structure we have in mind, with actions A1 to A4 facilitating action subgoals SG1 to SG3 which facilitate more basic goals G1 to G3. Not shown are coherence relations between actions that are jointly necessary, or incoherence relations among incompatible actions and goals. The arrows indicate that facilitation is typically unidirectional; a figure showing coherence relations would have bi-directional arrows. But as the example in the next section will show, facilitation need not be a one-way relation, since there can be pairs of goals that facilitate each other.

Figure 1. Structure of a sample goal hierarchy. A1 ... A4 are actions that facilitate subgoal actions SG1-SG3 which facilitate intrinsic goals G1...G3. Not shown are coherence relations among actions or incoherence relations among actions or goals.Principle 3, Incompatibility, establishes relations of incoherence between pairs of factors. Typically, these will be pairs of actions that are hard to do together. No one can simultaneously go to New York City and to London (strong incoherence), and for some, it is difficult to walk and chew gum at the same time (weak incoherence). Similarly, some goals are completely incompatible, while others are only moderately in conflict. It is difficult, although perhaps not impossible, for life to be both comfortable and exciting. For an interesting discussion of goal conflicts, see (Wilensky, 1983) .
Principle 4, Goal Priority, implies that different goals may have different inherent priority which should influence judgments of coherence. Inherent desirability can come from biological needs, indoctrination, social comparison, and possibly from other directions. The point is that intrinsic desirability is independent of the coherence considerations that govern acceptability of actions and subgoals, although coherence can have some effect on the ultimate impact of intrinsic goals too. An ascetic may have the same intrinsic need for food and sex as anyone else, but adoption of more spiritual goals may lessen the impact of physical goals on decision making.
Principle 5, Judgment, asserts that coherence of a plan is partly affected by the coherence in one's overall belief system of beliefs about what facilitates what. For example, Howard may believe that being at the more elite institution will make him more happy. But this belief may be undermined if he does a systematic comparison of people he knows and discovers that the people at the most elite institutions are not any happier than those at moderately elite ones. Deliberative coherence may therefore depend to some extent on belief coherence, assuming that the acceptability of beliefs is also a matter of coherence (Harman, 1976) .
Finally, the sixth principle, Decision, says that actions are chosen not in isolation, but as parts of complex plans that involve other actions and goals, with goals being partly revisable just like choices of actions.
First, actions and goals can be represented by units in a connectionist network. The representation is entirely localist, rather than distributed as is found in PDP networks using backpropagation. Second, whenever according to the above principles there is a coherence relation between actions or goals, there should be an excitatory link between the two units representing them. Similarly, incoherence relations that represent incompatible actions and goals can be represented by inhibitory links. Third, intrinsic desirability of some goals is easily implemented by linking a special unit, which is always active, to each unit representing an intrinsic goal. As with the links representing coherence and incoherence relations, there can be different weights on the links representing different degrees of desirability. Finally, with activation spreading from the special unit to the goals and then out to the subgoals and the actions, the network will update activation of the various units in parallel until all units achieve stable activation. The final activation of the units represents either the choice of particular actions or the posterior value of particular goals. Just as some actions are rejected in favor of better ones with which they compete, some goals are rejected or downplayed as part of the overall judgment of deliberative coherence. All links in this system are symmetrical, reflecting their implementation of considerations of coherence and incoherence. But the links from some of the goal units to the always-active special unit introduces an asymmetry of processing: goal units may much more of an effect on action units than vice versa, since activation can flow directly from the special unit to the units representing goals with inherent priority, and only then to units representing actions.
The computational model provides a means of testing out whether the principles of deliberative coherence can fruitfully be applied to understand real cases of complex decision making. After describing DECO in more detail, we will present a simple example to show how it makes coherence-based decisions and goal adjustments. Finally, we show how DECO is relevant to understanding some of the psychological limitations of standard decision theory.
There are four kinds of input statement to DECO, two to establish units representing the goals and actions, and two to establish links between those units.
1. Input (goal 'G description & optional priority) establishes G as a goal. This input creates a unit to represent G; the description is provided for informational purposes only. If the goal is known to have some inherent priority, then a value is given for the optional field priority, and the unit is linked with the special unit with an excitatory link proportional to the value priority, which ranges between 0 and 1.
2. Input (action ' A description) establishes A as an action, and it creates a unit to represent it.
3. Input (facilitate 'F1 'F2 degree) states that factor F1 facilitates F2 to the indicated degree, which can range between 0 and 1. To represent facilitation, an excitatory link is created between F1 and F2 proportional to the degree.
4. Input (incompatible 'F1 'F2 degree) states that F1 and F2 are incompatible to the indicated degree, which can range between 0 and 1. To represent incompatibility, an inhibitory link between F1 and F2 is created proportional to the degree indicated.
These four inputs create a set of units connected by excitatory and inhibitory links. The network can then be settled using a standard connectionist updating algorithm to adjust in parallel the activation of each unit, taking into account its links to other units and the activations of these units. (For details, see (Thagard, 1992) , p. 101). Initially, all units except the special unit have activations of 0, but in fewer than 100 cycles of updating they achieve stable activation levels between -1 and 1. After the network has settled, the final activation of each unit represents the desirability of the action or goal that it represents, with activation greater than 0 interpreted as acceptance, and activation less than 0 interpreted as rejection. Actions with high activation are the ones selected for initial performance. Goals with high activation are similarly parts of the plan to be executed. In addition, the final activation of the units representing goals represents their posterior importance, which may deviate from their initial intrinsic importance.
To be more concrete, let us consider a simulation of the dilemma facing Howard in the story at the beginning of this paper. Here is the input given to DECO:
(goal 'G1 "Increase scientific understanding." 1)This assumes that Howard has three goals of equal intrinsic importance; if we knew more about the relative importance of his goals, we could replace the occurrences of "1" with different values between 0 and 1. But it would be wrong to think of G4-G9 as simply subgoals to G1-G3, since some of the intrinsic goals can facilitate the others as well as vice versa. For example, increasing scientific understanding can produce excitement.(goal 'G2 "Keep family happy." 1)
(goal 'G3 "Keep self happy." 1)
(goal 'G4 "Comfort for self." )
(goal 'G5 "Comfort for family ." )
(goal ''G6 "Prestige.")
(goal 'G7 "Salary.")
(goal 'G8 "Excitement.")
(goal 'G9 "Intellectual environment.")
(action 'A1 "Move to new job.")Howard has two choices: move or stay. In this case, these are the basic actions and are clearly distinguishable from the goals. Sometimes, however, there is no real distinction between subgoals and actions, as when someone takes a bus to the airport as a subgoal to flying somewhere.(action 'A2 "Reject job offer.")
(facilitate 'G9 'G1 1)(facilitate 'G5 'G2 1)
(facilitate 'G3 'G2 1)
(facilitate 'G2 'G3 1)
(facilitate 'G4 'G3 1)
(facilitate 'G6 'G3 1)
(facilitate 'G7 'G3 1)
(facilitate 'G8 'G3 1)
(facilitate 'G1 'G6 1)
(facilitate 'G1 'G8 1)
Different goals contribute to other goals to varying degrees. Lacking detailed knowledge of Howard's goal structure, we assume that different subgoals facilitate different goals equally. With additional knowledge, values ranging from 0 to 1 could be substituted for each 1 above. Note that goals G2 and G3 facilitate each other: his family being happy helps to make him happy and vice versa. Note also that there are complex routes through the facilitation structure: G9 facilitates G1 which facilitates G6 and G8, which both facilitate G3. Although G1 is deemed to be intrinsically desirable, it can still facilitate other goals.
(facilitate 'A1 'G6 1)Different actions contribute directly to different goals to varying degrees, but we do not know enough about Howard's goal structure to discriminate finely. To get a crude picture, however, we have above included only facilitation statements where one of the actions clearly facilitates a goal more than the alternative action. The alternative would be to have a full set of facilitation statements with fanciful numbers. Our point here is that it is the coherence relations that matter more than the numbers, since people rarely know precisely the extent to which potential actions will contribute to their goals, although with experience they may learn to give useful estimates.(facilitate 'A1 'G7 1)
(facilitate 'A1 'G8 1)
(facilitate 'A1 'G9 1)
(facilitate 'A2 'G4 1)
(facilitate 'A2 'G5 1)
(incompatible 'A1 'A2 1)The two actions are strongly incompatible, since Howard cannot both move and stay. The two subgoals are only weakly compatible, since excitement and comfort are difficult to combine but not impossible.(incompatible 'G4 'G8 .5)
The input just given creates a network with the structure shown in figure 2, which makes it easy to see how the units representing A1 and A2 are linked to the subgoal units, and how the subgoal units are linked to the intrinsic goal units. All three intrinsic goal units are linked to the special unit. When the network is adjusted, activation spreads from the special unit to each of the goal units, then to the subgoals, then to the actions. But there is more to the decision than simply a downward spread of activation, since the units for A1 and A2 inhibit each other, as do the units for SG6 and SG7. Moreover, since the excitatory links are symmetrical, the action units affect the subgoal units as well as vice versa. The network is not simply selecting which action to do: it is simultaneously evaluating the goals and subgoals as well. A subgoal that coheres poorly with desirable goals and actions will be deactivated just as well as a non-preferred action. Figure 3, produced automatically when DECO is run, shows the activation trajectories of the units as the network settles. A1 is clearly preferred to A2 which is deactivated, receiving activation below 0. The various subgoals receive different degrees of activation depending on how well they cohere with actions, goals, and other subgoals. If, however, G4 and G5 are identified as being intrinsically desirable, then A2 is preferred to A1, since staying put makes a more direct contribution to comfort than moving.
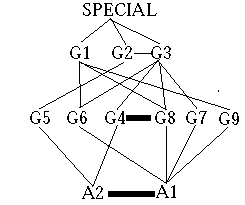
Figure 2. Network created by the input to the Howard example given above. Thick lines indicate inhibitory links. Thin lines indicate excitatory links. All links are symmetrical.
***MISSING FIGURE 3 ***
Figure 3. Graph of activation of the units in the Howard simulation. For each unit, the graph shows the activation starting at 0 (horizontal line) and proceeding until stable. Notice that A1 is chosen while A2 is rejected. G4 is much less favored than the other units because it conflicts with the more successful G8.DECO uses the same algorithm for parallel constraint satisfaction as ECHO, the program that inspired it. ECHO shows how hypotheses can be evaluated on the basis of evidence; units representing evidence are linked to the special unit. In DECO, the intrinsic goal units are roughly analogous to the evidence units in ECHO, providing a basis for choosing among actions and other goals. The hypothesis units in ECHO thus correspond roughly to the action and non-intrinsic goal units in DECO.
It might appear from the simple example given above that DECO could be replaced by a simple calculation. The value of each goal or action could be easily calculated from the value of each intrinsic goal it facilitates. But this would neglect the fact that what is being computed is an overall judgment of coherence: the point is not just to choose actions, but to put together a total package of goals and actions. The simple calculation approach cannot capture the way in which decision making involves selecting goals as well as actions. Similarly, in ECHO the point is not just to select hypotheses, but also to evaluate the credibility of the evidence. Intrinsic goals, like evidence, have a large degree of independent acceptability, but are subject to reevaluation and even rejection.
The Howard example does not illustrate several properties of DECO inspired by the principles of deliberative coherence. It does not have cases where multiple actions together facilitate a goal, so it does not illustrate principles 2(b) and 2(c). And the example does not show how factual judgments can enter into decision making in accord with principle 5. DECO has been applied to several more complex cases of decision making than the basic Howard case, but rather than present more examples we want to discuss how our deliberative coherence perspective on decision making differs from the classical perspective.
This notion of utility is very different from the original notion used by early theorists such as Bernoulli and Bentham, who treated utility as a matter of subjective experience rather than a mathematical construction (Cooter & Rappoport, 1984; Kahneman & Snell, 1990) . Derived utility was devised in the 1930s and 1940s in keeping with the behaviorist spirit of the times, to which experienced utility seemed to be an unjustifiable mental hypothesis. Utility became theoretically respectable once it was conceived as a numerical quantity derived from preferences that in turn could be derived from observed choices, rather than as a feature of mental experience. Unfortunately, the notion of utility thereby lost any explanatory value: on the original view of utility, we can say that someone prefers x to y because the former has greater utility than the latter, but such explanations are vacuous if utility is just a way of summarizing preferences. For classical decision theory and the microeconomics that is so heavily based on it, preferences are basic and mysterious.
In contrast, the theory of deliberative coherence (TDC) and DECO are intended to explain why we have the preferences we have. Eschewing behaviorist strictures on postulating mental representations, TDC assumes that humans have multiple interrelated goals that determine what actions are preferred. Such assumptions are of course standard in contemporary cognitive science, where intelligent behavior is explained in terms of the mental structures and processes that produce the behavior. Whereas original, pre-behaviorist utility theory explained preferences on the basis of a single mental quantity, utility, TDC invokes multiple interrelated goals to account for peoples' actions. Moreover, in contrast to theories of multi-attribute decision making that postulate people's use of various pre-established criteria, TDC allows that goals and subgoals are also up for grabs and can be adjusted during the decision making process. Goals are not given to us absolutely: we have to learn how important different goals are to us over time.
Our view of decision making runs contrary to traditional conceptions according to which we do not deliberate about ends but always about means and that deliberation is guided by a single ultimate end such as happiness or pleasure. Kolnai offers a more psychologically acute picture of human deliberation that portrays the meagreness of the means-ends conception (Kolnai, 1978) . In our terminology (in which actions and goals correspond to means and ends), we follow Kolnai in noticing that humans have multiple goals, some of them consonant with each other but others that are mutually contrary, jarring, and discordant. We not only choose actions to accomplish goals, we sometimes look round for goals to be achieved by the actions at our disposal. For example, a runner who likes to run every day may adopt the goal of running in a marathon. Running every day facilitates running the marathon, not the other way around, but here the goal is adopted to fit the means for accomplishing it. People have a deep need to adopt goals that provide them with a sense of purpose and unity to their lives (Frankfurt, 1992; Harman, 1976; Schmidtz, forthcoming) .
This kind of goal-creation does not make sense from an instrumentalist perspective on decision making, but it does from a coherentist perspective such as ours. DECO does not address the question of how new goals are introduced into the system, any more than ECHO addresses the question of how hypotheses and relations among them are discovered. But DECO does show how adopting a new goal can increase the overall coherence of a system of goals. Consider, for example, an academic who feels a conflict between the goal of being a good teacher and the goal of excelling at research. Given the time involved in these two pursuits, there is at least a weak incompatibility between the goals. But the academic might decide to write a book based on a course frequently taught. Publishing the book would facilitate the academic's research reputation, but writing the book would both facilitate teaching and be facilitated by it. The facilitation structure is shown in figure 4. Introducing the goal of writing the book introduces coherence between the goals of teaching and research that otherwise would be discordant. Similarly, many people feel a conflict between pursuing their careers and spending time with their families. Coherence can be introduced into the system of goals by supposing that career success contributes both to family income and happiness of the worker, both of which may facilitate family happiness. In the other direction, spending time with the family can be good recreation which enhances career performance. The overall structure is shown in figure 5. From an instrumentalist point of view, this looks hopelessly circular, but it is unproblematic in a coherence account such as DECO assumes, since all the facilitation relations get translated into symmetric links: everything fits together. Circularities are not a problem in a coherence account. I may start off with a goal to survive, from this acquire a goal to buy food, from this acquire a goal to get a job, but then discover that the job is so enjoyable that I want to survive so that I can still have the job (Schmidtz, forthcoming) . The original goal of surviving becomes a subgoal for the subgoal of having a job. The circle is non-vicious, however, if one simply assumes that the system is driven in the direction of increasing the coherence of its actions and goals, rather than toward some ultimate goal. We conjecture that subjective well-being is as much a matter of coherence among one's actions and goals as it is a matter of accomplishing goals. Additional philosophical issues relevant to deliberative coherence are discussed elsewhere (Millgram & Thagard, forthcoming) .
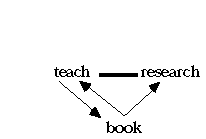
Figure 4. Incompatible goals (indicated by thick line) unified by facilitation relations (thin lines with arrows).
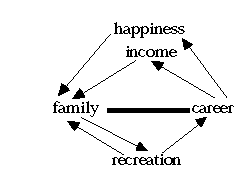
Figure 5. Another example of incompatible goals (indicated by thick line) unified by facilitation relations (thin lines with arrows).We obviously have a long way to go, however, to show that the theory of deliberative coherence is a genuine alternative to the elegant and ubiquitous classical theory of decision. We have not shown in this paper how TDC and DECO can model human divergence from the axioms of utility theory, although we have rough simulations of some of the phenomena such as intransitivity of preferences. Nor have we said enough about how the goal structures and facilitation relations that go into DECO arise in the first place. Still, we have pointed the way toward further development of a non-instrumentalist, coherentist theory of decision making.
Let us distinguish between three ways in which goals can affect inferences, which can be described as being goal-relevant, goal-influenced, and goal-determined. In any real system, as opposed to a logical abstraction, all inference including deductive and inductive inference must be constrained by goal-relevance (Harman, 1986; Holland, Holyoak, Nisbett, & Thagard, 1986) . Otherwise, the inferential and problem solving capacities of the system will be overwhelmed with useless junk. But to make inductive inferences goal-determined would be to risk falling into wishful thinking, believing something just because it suits our personal goals to do so. It is legitimate for decisions to be goal-determined, but deductive and inductive inferences need to be based on evidence, even if goals affect what is deemed to be relevant to infer. In fact, decisions are not exclusively goal-determined, since they will depend in part on judgements of fact as allowed in principle 5 of TDC; this is captured in DECO by the need for input statements that represent empirical estimates of what facilitates what.
The intermediate category, goal-influenced inferences, is trickier to characterize. Ziva Kunda's theory of motivated inferences shows how inductive inferences can be goal-influenced while not completely goal-determined (Kunda, 1987; Kunda, 1990) . Her experiments show that people's inferences can be biased by their personal goals, but the bias is more subtle than simple wishful thinking. Rather, if people have goals that make them want to believe P, they may do selective search of their memories that turns up evidence for P. Goals do not directly influence the inference from the evidence to the conclusion, but they affect what evidence is considered in the inference. Thus scientists arguing over alternative theories may bring different kinds of evidence to bear in favor of their preferred theories.
Our development of the theory of deliberative coherence and the computational model DECO has displayed interesting parallels between decision making (practical inference) and hypothesis evaluation (theoretical inference), where the latter is understood in terms of explanatory coherence and ECHO. Theoretical inference will necessarily feed into practical inference as judgments of fact are needed to help affect judgments of facilitation that are crucial to establishing deliberative coherence. But how deliberative coherence can or should influence explanatory coherence remains to be determined.
Frankfurt, H. (1992). On the usefulness of final ends. Iyyun, The Jerusalem Philosophical Quarterly (41 (January)), 3-19.
Harman, G. (1986). Change in view: Principles of reasoning. Cambridge, MA: MIT Press/Bradford Books.
Harman, G. (1976). Practical reasoning. Review of Metaphysics, 29, 431-463.
Hausman, D. M. (1992). The inexact and separate science of economics. Cambridge: Cambridge University Press.
Holland, J. H., Holyoak, K. J., Nisbett, R. E., & Thagard, P. R. (1986). Induction: Processes of inference, learning, and discovery. Cambridge, MA: MIT Press/Bradford Books.
Kahneman, D., & Snell, J. (1990). Predicting utility. In R. M. Hogarth (Eds.), Insights in decision making (pp. 295-310). Chicago: University of Chicago Press.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica, 47, 263-291.
Kolnai, A. (1978). Deliberation is of ends. In Ethics, value, and reality (pp. 44-62). Indianapolis: Hackett.
Kreps, D. M. (1990). A course in microeconomic theory. Princeton: Princeton University Press.
Kunda, Z. (1987). Motivation and inference: Self-serving generation and evaluation of causal theories. Journal of Personality and Social Psychology, 53, 636-647.
Kunda, Z. (1990). The case for motivated inference. Psychological Bulletin , 108, 480-498.
Millgram, E., & Thagard, P. (forthcoming). Deliberative coherence.
Schmidtz, D. (forthcoming). Why be moral? Princeton: Princeton University Press.
Thagard, P. (1989). Explanatory coherence. The Behavioral and Brain Sciences, 12, 435-502.
Thagard, P. (1992). Conceptual revolutions. Princeton: Princeton University Press.
Tversky, A., & Kahneman, D. (1981). The framing of decisions and the psychology of choice. Science, 211, 453-8.
Wilensky, R. (1983). Planning and understanding. Reading, MA: Addison-Wesley.