Orthographic Processing in Visual Word Recognition:
A Multiple Read-Out Model
Jonathan Grainger1 & Arthur M. Jacobs2
1 Centre de la Recherche en Psychologie Cognitive
Centre National de la Recherche Scientifique (C.N.R.S.)
Université de Provence
Aix-en-Provence, France
2 Department of Psychology
Philipps-University,
Marburg, Germany
and
Centre for Research in Cognitive Neuroscience,
Brain & Language Group
Centre National de la Recherche Scientifique (C.N.R.S.)
Marseille, France
Short title: Orthographic Processing and Word Recognition
Address: CREPCO, Université de Provence, 29 Avenue Robert Schumann,
F-13621 Aix-en-Provence.
Email: Grainger@univ-aix.fr or Jacobs@lnf.cnrs-mrs.fr
ABSTRACT
A model of orthographic processing is described that postulates read-out from different information dimensions, determined by variable response criteria set on these dimensions. Performance in a perceptual identification task is simulated as the percentage of trials on which a noisy criterion set on the dimension of single word detector activity is reached. Two additional criteria set on the dimensions of total lexical activity and time from stimulus onset are hypothesized to be operational in the lexical decision task. These additional criteria flexibly adjust to changes in stimulus material and task demands, thus accounting for strategic influences on performance in this task. The model unifies results obtained in response-limited and data-limited paradigms, and helps resolve a number of inconsistencies in the experimental literature that cannot be accommodated by other current models of visual word recognition.
When skilled readers move their gaze across lines of printed text in order to make sense of letter sequences and spaces, it is very likely that for each word an elementary set of operations is repeated in the brain. These operations compute a form representation of the physical signal, match it with abstract representations stored in long-term memory, and select a (best) candidate for identification. This basic process, generally referred to as word recognition (although the terms word identification and lexical access are popular synonyms), has been one of the major issues in cognitive psychology in the last two decades (for review see Carr & Pollatsek, 1985; Jacobs & Grainger, 1994).
Word recognition is an integral component of language processing in general. It raises a fundamental question about the functioning of the brain: How is previously stored information about an input pattern organized and how is it retrieved? In this respect, lexical processing is well-suited to experimental and theoretical study, because words form a well-structured and easily manipulated set of patterns (Forster, 1992). In particular, languages with alphabetic orthographies have the advantage of providing a simple metric for measuring formal similarities between words (Grainger, 1992). Our knowledge about the orthographic structure of a language, based on statistical analyses of a word corpus, allows us to ask precise questions with respect to the structure of the mental representations mediating word recognition and the nature of the procedures involved. Such analyses make it possible to examine, for example, whether word recognition time and/or accuracy is influenced by words that are orthographically similar to the target word (Andrews, 1989; 1992; Grainger, O'Regan, Jacobs & Segui, 1989; 1992; Sears, Hino, & Lupker, 1995; Snodgrass & Mintzer, 1993). In addition, the use of sophisticated simulation models, such as the interactive activation model (McClelland & Rumelhart, 1981), that incorporate their own orthographic lexicon and a particular orthographic metric, enables us to test hypotheses about the structure and dynamics of orthographic processing at the level of fine-grained analysis, thus deriving predictions for individual items (Coltheart & Rastle, 1994; Grainger & Jacobs, 1994; Jacobs & Grainger, 1991; 1992; Norris, 1994; Paap & Johansen, 1994).
In this article, we present a formal account of orthographic processing in visual word recognition which provides insights into the microstructure and dynamics of information processing in different experimental paradigms. Our approach yields a broad scope of theoretically meaningful measures that can enter into quantitative comparisons across conditions and experiments. We believe that in order to facilitate theory construction and falsification in cognitive psychology, models of information processing designed to predict a single dependent variable in a single experimental paradigm (e.g., the many extant models designed to predict mean reaction time (RT) in the Sternberg, 1966, paradigm, or the many models designed to explain the word superiority effect in the Reicher-Wheeler paradigm, Reicher, 1969; Wheeler, 1970) will progressively be replaced by, or extended to, models that make explicit assumptions about the microstructure and dynamics of processing and that generalize across dependent variables (accuracy, RT means and distributions) and across paradigms (cf. Jacobs & Grainger, 1992; 1994; Ratcliff, 1978). Apart from the difficulty of interpreting mean RT data for accuracy levels near ceiling (Jonides & Mack, 1984; Pachella, 1974), models that predict only mean RT are inadequate to account for the dynamics, because they can be contradicted by further analyses of RT data (Ratcliff & Murdock, 1976). We therefore argue that an adequate model of choice RT in the lexical decision task for example, should allow predictions about RT distributions, speed-accuracy trade-off (SATO) and error rates. Such a facility has repeatedly proven useful in deciding between models (McClelland, 1979; Mewhort, Brown, & Heathcote, 1992; Murdock & Dufty, 1972; Ratcliff, 1978; Ratcliff & Van Zandt, 1995; Roberts & Sternberg, 1993; Van Zandt & Ratcliff, 1995). In the following section, we discuss what in our view are some of the key issues for the future development of models of visual word recognition in particular, and models of human cognition in general.
Strategies for Model Construction
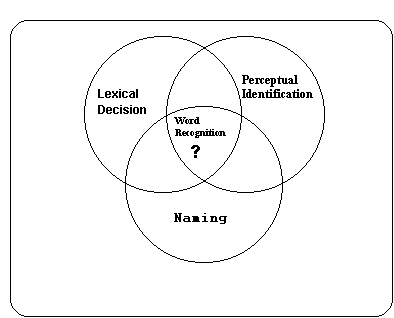
In a recent paper (Jacobs & Grainger, 1994), we laid out three strategems for model construction in the field of visual word recognition: Modeling functional overlap, canonical modeling, and nested modeling. All three strategems are applied in the present work in an attempt to identify the core processes underlying word recognition by building multilevel, multitask models (Jacobs, 1994). This modeling approach is designed to facilitate the development of an internally and externally constrained (Kosslyn & Intrilligator, 1992; Posner & Carr, 1992), integrated model of visual word recognition (Jacobs, 1994). The cornerstone of our approach is the concept of functional overlap, illustrated in Figure 1. This concept relates the ideas that i) there is a reasonable overlap between the functional mental structures and processes involved in making perceptual identification, lexical decision, or naming responses, and those involved in identifying isolated words, and ii) there is no model-free way of determining this functional overlap.

Figure 1. Venn diagram illustrating the concept of functional overlap.
A straightforward way of modeling functional overlap is to construct, on the basis of a computational theory in the sense of Marr (1982), or a set of sufficiently constraining background assumptions (Posner & Carr, 1992), a readily falsifiable performance or algorithmic-level model of a task A. After testing the model in task A, we eliminate the postulated task-specific process(es) and test it in a related task B, which, by hypothesis, is otherwise identical to A. If the model does well in predicting performance in both tasks, it is reasonable to assume that the difference between the two tasks is well captured by the postulated task-specific process(es), and that the model captures the basic, task-independent representations and processes (Jacobs, 1994).
In the present work we attempt to relate performance in two of the three tasks represented in Figure 1 (lexical decision and perceptual identification) to the core processes of visual word recognition. For this purpose, we assume that in the perceptual identification task two of the three processes underlying performance in the Yes/No lexical decision task are not operational. The choice of these two particular tasks will help correct the recent bias in the word recognition literature which clearly is in favor of models of word naming (e.g., Coltheart, Curtis, Atkins, & Haller, 1993; Seidenberg & McClelland, 1989). Moreover, leaving out the word naming task allows us to focus on orthographic processing in visual word recognition.
The second stratagem applied in the present work is canonical modeling (Stone & Van Orden, 1993; 1994). The cornerstone of this approach to theory development is a refinement process that starts with the simplest model within a given framework that fairly characterizes the qualitative behavior of other models that share its design and system principles with respect to the data at hand (e.g., the interactive activation (IA) model as the prototype of a canonical resonance model). The aim of this modification and refinement process is to identify modeling principles and to determine the explanatory credit and blame with respect to these principles. In previous related work we have systematically tested the system principles (i.e., architectural principles that determine the behavior of a class of models) of lateral inhibition (Grainger & Jacobs, 1993), and interactivity (Grainger & Jacobs, 1994; Jacobs & Grainger, 1992; see also Stone & Van Orden, 1994 for a discussion of the advantages of this approach). In the present work we concentrate on testing design principles, which determine the relationship between the behavior of a (class of) model(s) and the observed dependent variables. The assumptions of variable decision criteria, and multiple read-out, discussed below, are such design principles, whose validity can be tested directly.
The third stratagem followed in the present work is nested modeling, that is, a new model should either include the old one(s) as a special case, or dismiss with it, after falsification of the core assumptions of the old model. According to the criteria discussed in Jacobs and Grainger (1994), the present multiple read-out model represents the most general case of connectionist models of the IA family (McClelland & Rumelhart, 1981; Rumelhart & McClelland, 1982), and it includes the semistochastic interactive activation model (SIAM: Jacobs & Grainger, 1992), and the dual read-out model (Grainger & Jacobs, 1994) as special cases. Finally, in relation to the two latter strategems, the present work applies the "minimal structure principle" of modeling, i.e., always start with the simplest possible model and see how far one can get with that.
The Multiple Code Activation Hypothesis
Like many students of modern reading research, we adopt the standard assumption that the presentation of a word results in the computation of several types of information (or codes) in parallel (Carr, 1986; Carr & Pollatsek, 1985; Donnenwerth-Nolan, Tanenhaus, & Seidenberg, 1981; Morton, 1969). The role of orthographic, phonologic, and semantic codes has been well studied within the functional context of the lexical decision task, and, as recently argued convincingly by Posner and Carr (1992), all three codes can be, but not necessarily are, used in combination to make a visual lexical decision (cf. Seidenberg & McClelland, 1989). Indeed, there is considerable evidence from recent studies using both behavioral and brain imaging techniques that both orthographic and phonological codes are available in the very earliest stages of processing printed strings of letters (Compton, Grossenbacher, Posner, & Tucker, 1991; Ferrand & Grainger, 1992; 1993; Lukatela, Lukatela, & Turvey, 1993; Lukatela & Turvey, 1990; Perfetti & Bell, 1991; Posner & Carr, 1992; Posner & McCandliss, 1993; Waters & Seidenberg, 1985; Ziegler & Jacobs, 1995; Ziegler, Van Orden, & Jacobs, 1996).
Applying the modeling strategies discussed above, in the present work we make the simplifying assumption that in many conditions the orthographic code is sufficient to make a visual lexical decision response (see Coltheart, Davelaar, Jonasson, & Besner, 1977, and Seidenberg & McClelland, 1989, for a similar assumption). We make the same assumption with respect to performance in tasks using data-limited procedures (e.g., the perceptual identification task, the Reicher-Wheeler task). In applying this general research strategy, the present approach is motivated by the goals of parsimony and falsifiability. Including all possible levels of representation (e.g., phonological and semantic codes) into a model of the IA family requires a great deal of auxiliary assumptions that are weakly constrained by our knowledge about the nature and connectivity of such units (cf. Posner & Carr, 1992). We have no standard metric yet for phonological units involved in visual perception (e.g., phonemes, syllables) and totally ignore what kind of meaning representation could be used in the lexical decision task (Paap, McDonald, Schvaneveldt, & Noel, 1987). Thus, in accord with the stratagems of canonical modeling and nested modeling discussed above, as well as the minimal structure principle, the present work illustrates how such a minimalist model can explain a large variety of critical results in the field of visual word recognition.
In summary, it should be stressed that we do not deny the possibility that phonological, semantic, or other codes, can affect performance in the perceptual identification and lexical decision tasks. We chose to follow a logic that starts with a simple but detailed and precise model and explores the range of complex behavior for which it can provide a principled account. Occam's razor counsels us not to multiply entities (e.g., processing levels and units) beyond necessity. Necessity is a function of the range of facts to be explained (the model's scope) without increasing auxiliary assumptions (Jacobs & Grainger, 1994). The present model strikes a good balance between simplicity and scope, that would have been severely compromised if we had included phonological and semantic units right from the start.
The Lexical Inhibition Hypothesis
Our central theoretical claim with regard to how the orthographic (input) lexicon is structured and how word recognition is achieved is a "connectionist" one in the sense that it is derived from the first operational connectionist model of letter and word perception, the IA model (McClelland & Rumelhart, 1981; Rumelhart & McClelland, 1982). According to what we have termed the connectivity assumption (Jacobs & Grainger, 1992) and the lexical inhibition hypothesis (Grainger & Jacobs, 1993), the multiple orthographic representations that are contacted during the visual recognition of isolated words and letter strings compete in the identification of the stimulus. This postulated mechanism of competition between localist lexical representations is resolved via inhibitory connections. These inhibitory connections implement a best match strategy of selecting a representation for output processes (Jacobs & Grainger, 1992; McClelland, 1987; see McClelland, 1993, for a general discussion of the issue of mutual competition).
An important current issue in the field of auditory word recognition is whether word recognition is achieved via inhibitory connections or via a decision mechanism that uses a relative goodness rule to convert the activation value of some representation into a response probability (Bard, 1990; Eberhard, 1994; Frauenfelder & Peeters, 1990; 1994; Goldinger, Luce, & Pisoni, 1989; Goldinger, Luce, Pisoni, & Marcario, 1992; Marslen-Wilson, 1990; McQueen, Norris, & Cutler, 1994). This distinction allows testing between two types of parallel activation model of spoken word perception, the cohort model (Marslen-Wilson, 1987, 1990; Marslen-Wilson & Welsh, 1978) and the TRACE model (McClelland & Elman, 1986).
A similar issue arises when comparing the logogen and IA models of visual word recognition. The first incorporates the lexical independence assumption and the latter the lexical inhibition assumption. We have previously argued that the inhibitory effects of neighborhood frequency (Grainger, 1990; Grainger & Segui, 1990; Grainger et al., 1989; 1992) and masked orthograhic priming (Segui & Grainger, 1990) are best explained by the lexical inhibition hypothesis. In support of this we demonstrated that the SIAM can simulate these results (Jacobs & Grainger, 1992). The lexical inhibition hypothesis was also successfully applied to account for masked partial-word priming effects obtained in the lexical decision task (Grainger & Jacobs, 1993). In this study, we observed that the amount of facilitation produced by a partial prime (a prime that shares some of the target's letters) was strongly correlated with the positional letter frequencies of the prime's component letters. The higher the positional frequencies of letters shared by prime and target, the smaller the resulting facilitation. Positional letter frequency measures the number and the frequency of occurrence of all words (of a fixed length) that contain a given letter in a given position. In an IA model, positional letter frequency will therefore index the number of other words (and their activation levels) that are pre-activated by the prime stimulus and that continue to be activated on target presentation. The higher the positional frequencies of letters shared by prime and target, the stronger the inhibitory component of the resulting effects. In visual and auditory word recognition, both empirical and computational evidence is accumulating in favor of the lexical inhibition hypothesis. This also appears to be true in the area of language production (e.g., Berg & Schade, 1992; Schade & Berg, 1992).
A very simple test of the importance of lexical inhibition within the interactive activation framework consists in removing the inhibitory connections between word units. The resulting model can be thought of as a logogen-type parallel activation model that implements the lexical independence hypothesis. When tested with the stimuli used by Segui and Grainger (1990), this model incorrectly predicts that high-frequency orthographically related primes should produce facilitatory rather than inhibitory effects compared to unrelated control primes. In contrast, the SIAM successfully simulated these results (Jacobs & Grainger, 1992). Apart from the presence/absence of lexical inhibition, the logogen-type model was identical to the interactive version of the SIAM. One might object that this is not the right way of testing the model because the logogen variant might do better (or worse) with a different parameter set. However, when we first implemented the SIAM by extending the IA model (Jacobs & Grainger, 1992), we did not change a single of the original parameters, although we changed the lexicon, and the decision mechanism of the original IA model. Parameter tuning in models of the size and complexity of the IA model is a tedious and lengthy enterprise. Moreover, retuning parameters in an attempt to bring the original model in line with some (new) data also requires, in our opinion, that one shows that the new parameter set can still handle the original data, for which the model was designed in the first place. Following Estes' (1975; 1988) recommendation of testing competing models that differ with respect to a single critical feature (see also Jacobs & Grainger, 1992; 1994; Massaro & Friedman, 1990), we consider the present testing procedure to be the most appropriate.
According to our account of orthographic processing in visual word recognition, many correct responses to word stimuli in a perceptual identification and a lexical decision task, will be made when the appropriate whole-word orthographic representation reaches a critical level of activation, referred to as the word unit or M criterion. This will arise on a certain percentage of trials in a perceptual identification experiment as a function of stimulus exposure duration and degree of masking. It is assumed that on presentation of the backward mask, the activation levels of features that are compatible with the target start to decay, thus producing a gradual decrease in feature-to-letter excitation. In such a situation, the activation levels of compatible letter and word units continue to rise to a peak and then drop off to resting level. According to the variable criteria hypothesis, the value of the M criterion varies normally from trial-to-trial around a fixed mean value (Jacobs & Grainger, 1992). Therefore, the maximum activation attained by the most activated word unit will sometimes be greater and sometimes less than the value of the M criterion on a given trial in the perceptual identification paradigm. It is the number of times that this maximum activation value is greater than or equal to the M criterion that gives percent correct performance over a series of trials.
The multiple read-out hypothesis states that a response in a given experimental task is generated (read-out) when at least one of the codes that is appropriate for responding in that task reaches a critical activation level. It is further hypothesized that in certain tasks and certain experimental conditions more than one code can serve as the basis for generating a correct response to a printed word stimulus. Thus, in our dual read-out model of performance in the Reicher-Wheeler task (Grainger & Jacobs, 1994), the correct choice among two alternative letters presented in a briefly displayed word stimulus can be generated either by the appropriate letter representation or the appropriate word representation reaching a critical activation level. This aspect of the model allowed us to capture the influence of whole-word report accuracy on the magnitude of the word superiority effect (the superior forced choice accuracy to letters presented in words compared to pseudowords). In the present work we apply the general principle of multiple read-out as embodied in the dual read-out model.
The principle of multiple read-out is particularly relevant to our explanation of performance in the lexical decision task. With respect to this particular task, we hypothesize that unique word identification is not the only process that can lead to a correct "yes" decision in the lexical decision task, and that an extra-lexical process controls the production of "no" responses. In the functional context of the lexical decision task, word-nonword discrimination requires that participants use a reliable source of information that allows them to make rapid and accurate judgments concerning the "word-likeness" of stimuli (e.g., their familiarity / meaningfulness, Balota & Chumbley, 1984). Lexical decision therefore does not necessarily require (complete) identification of the word stimuli. Thus, several authors have proposed that a lexical decision can be made before word recognition has been completed. Some have hypothesized that the information used to make a correct decision is extra-lexical (Besner & McCann, 1987; Feustel, Shiffrin, & Salasoo, 1983). Other authors have proposed that an intra-lexical source is used (Balota & Chumbley, 1984; Gordon, 1983; Seidenberg & McClelland, 1989), and that extra-lexical sources of familiarity knowledge actually have little influence on lexical decision (Den Heyer, Goring, Gorgichuk, Richards, & Landry, 1988; Monsell, 1991).
In the present model, we postulate three processes underlying a speeded binary lexical decision response (see Appendix for a detailed description of the implemented decision criteria). Two of the processes use intra-lexical information to generate a "yes" response, and the third uses extra-lexical information to generate a "no" response. The two intra-lexical sources of information are: i) the overall (global) activity in the orthographic lexicon, operationalized in the simulation model as the sum of the activation levels of all word units, hereafter referred to as
s, and ii) the (local) activity of functional units within the lexicon, operationalized as the activation level of individual word units, or µ. The extra-lexical source of information is time (t) from stimulus onset. Note that the decision process operating on s can be compared to a fast-guess mechanism, present in many speeded response paradigms (e.g., Meyer, Osman, Irwin, & Kounios, 1988). These assumptions are tested in Experiments 1 to 3.
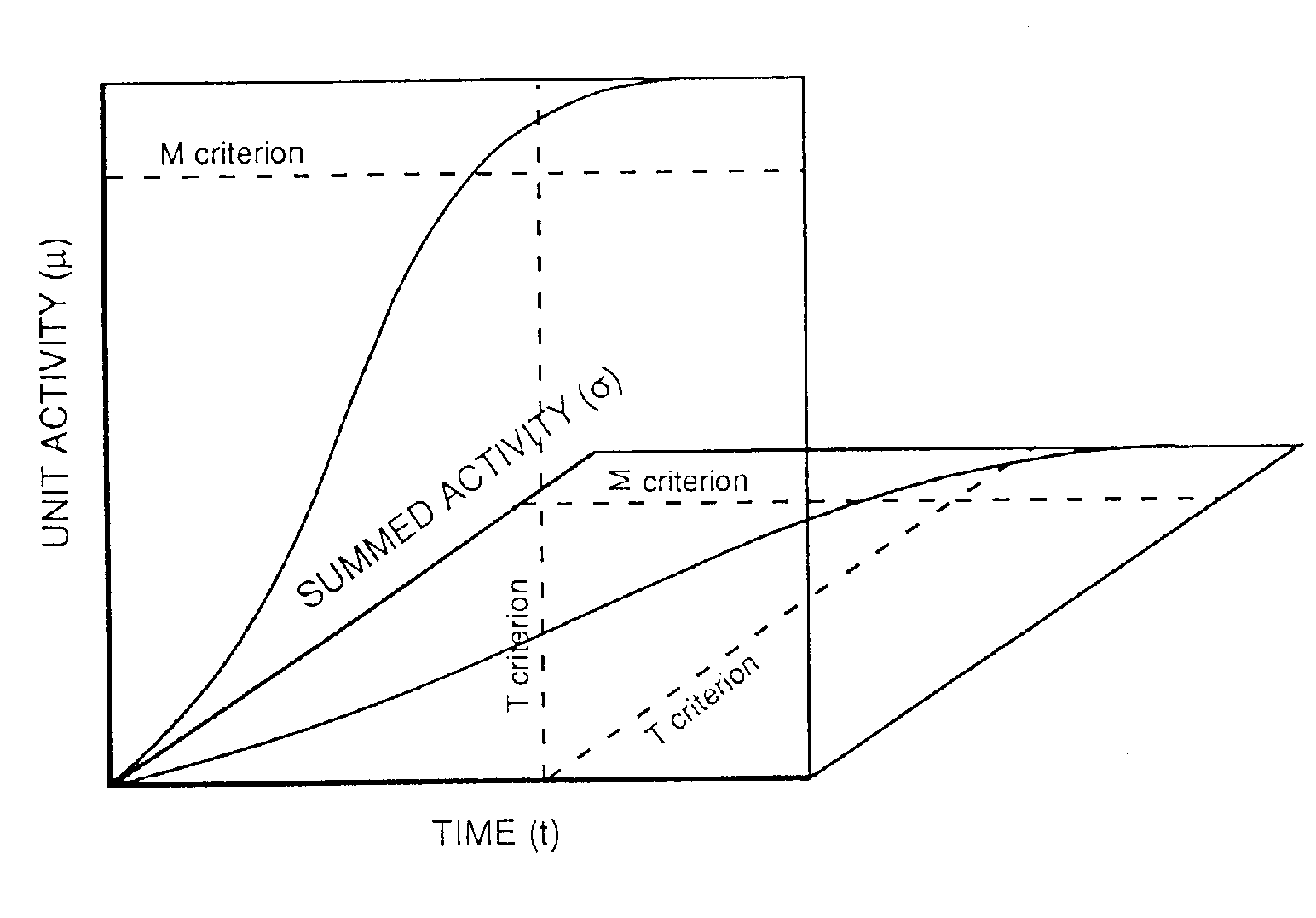
Figure 2. Application of the multiple read-out model to the lexical decision task. Three response criterion M, ∑, and T are set on three information dimensions: i) unit activity in the mental lexicon (µ), ii) summed lexical activity (
s), and iii) time (t). Increases in µ and s over time follow the sigmoid function of an interactive activation network (McClelland & Rumelhart, 1981). In general, word recognition is said to occur when the M criterion is reached, whereas a positive lexical decision response can be triggered when either the M or the ∑ criteria is reached before the T criterion. A negative lexical decision response is given in the converse situation.
In the multiple read-out model, a criterion value set on each of the three information dimensions determines the type (yes/no) and speed of a response. The criterion on the (local) µ dimension is referred to as M, the criterion on the (global)
s dimension as ∑ and the temporal deadline as T. Figure 2 illustrates how these three response criteria combine to determine the type and the speed of a response in the lexical decision task. If either the local M or the global ∑ response criteria are reached before the T criterion then a positive response is given, otherwise a negative response is given. Errors to word stimuli (false negatives) therefore arise when the T criterion is set too low and/or both the M and ∑ response criteria are set too high. Errors to nonword stimuli (false positives) arise in exactly the opposite circumstances (high T criterion and/or low M criterion or low ∑ criterion). In the example given in Figure 2, both the M and the ∑ response criteria are reached before the T criterion giving rise to a positive lexical decision response. The speed of this response is determined by the earliest moment in time that either the M criterion is reached (i.e., a specific word has been identified), or the ∑ criterion is reached (i.e., a fast guess has occurred). Response time for a negative response is simply given by the value of the T criterion.All three response criteria are noisy in that they vary normally from trial to trial around a mean value. Mean values of the three criteria can either be fixed or strategically variable. In particular, the M criterion is assumed to be fixed, because it is operational in the process of normal, automatic word recognition. We assume that normal word recognition is not under strategic control in the sense that participants cannot speed or slow this process voluntarily by shifting a response criterion. On the other hand, both the ∑ and T criteria are adjustable. Two main factors influence these criteria, one is stimulus driven, and the other is task-dependent. These are: i) the distributions of the
s values generated by words and nonwords during an experiment, and ii) task demands concerning speed and accuracy. These two factors are assumed to modify the critical mean value of both the ∑ and T decision criteria in the following way. In early phases of stimulus processing, the computed s value indexes the likelihood that the stimulus is a word. A high s value in early processing will encourage participants to set a longer deadline, i.e., a higher T criterion (Coltheart et al., 1977; Jacobs & Grainger, 1992), and a lower ∑ criterion. As concerns task demands, both the T and ∑ criteria are set higher when accuracy is stressed, and lower when speed is stressed. The higher the T criterion, the less false negative errors. The higher the ∑ criterion, the less false positive errors. A critical aspect of our lexical decision model concerns the fact that the ∑ and T decision criteria are conjointly modifiable by the same (intra- and extra-lexical) information sources. As will be seen in the following simulation studies, this has important consequences for the model's ability to account for SATOs observed in the lexical decision task.Figure 3 illustrates how variations in the ∑ criterion affect responses to word and nonword stimuli in the multiple read-out model (for simplicity the T criterion is fixed in these examples). Stimuli that generate a relatively low
s value in early phases of processing (e.g., the word BLUR and the nonword FLUR), maintain a high average value of the ∑ criterion. In this case, a correct positive response to a word stimulus is
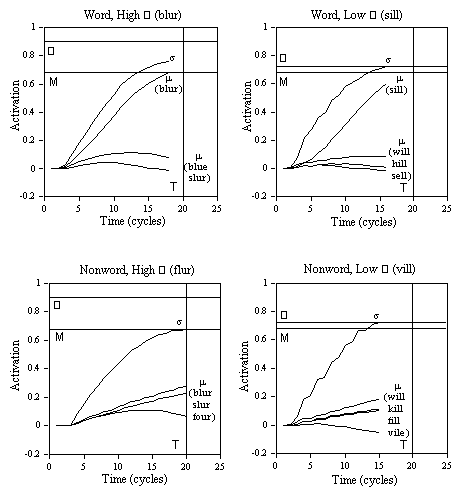
Figure 3. Example simulations showing variations in summed (
s) and unit (µ) lexical activity over time with word and nonword stimuli that generate either a low or a high ∑ criterion. The M criterion is fixed at 0.68 and the T criterion at 20 cycles. Processing stops when either the M, ∑, or T criterion is reached. Unit activity is shown for the target word and some other activated words.
generated by the M criterion, and a correct negative response to a nonword stimulus is generated by the T criterion. On the other hand, stimuli that generate a high
s value in early phases of processing (e.g., the word SILL and the nonword VILL), give rise to a lower average value of the ∑ criterion. This generates faster correct positive RTs to word stimuli, and increases the number of false positive errors to nonword stimuli.Specific assumptions concerning the use of multiple criteria or thresholds have been made in many other theories and models of information processing (e.g., Krueger, 1978; Ratcliff, 1978) and word recognition (e.g., Atkinson & Juola, 1973; Balota & Chumbley, 1984; Paap et al., 1982). Our motivation for postulating three processes with variable decision criteria was twofold. The first is scope, since it allows us to predict a total of six dependent variables measured in lexical decision and perceptual identification tasks. These are: a) means and distributions of RTs to word stimuli; b) means and distributions of RTs to nonword stimuli; c) mean percent error to word stimuli (miss rate); d) mean percent error to nonword stimuli (false alarm rate); e) means and distributions of RTs to misses; f) means and distributions of RTs to false alarms. In the lexical decision task distributional data are available for both correct and incorrect responses and the overall pattern of results surely imposes a considerable degree of constraint on any model of this task. We feel that such a high degree of constraint is very useful when modeling speeded RT tasks (cf. Ratcliff, 1978). Given the current trend in cognitive psychology towards complex algorithmic models, multiple constraint analyses including RT distributions and error rates will become increasingly important for choosing between models (Jacobs & Grainger, 1994; Roberts & Sternberg, 1993). McClelland (1993) has recently challenged network modelers to provide models, adhering to his GRAIN principles, that can account for data from RT paradigms (as opposed to the Asymptotic Choice and Time-Accuracy paradigms that, according to McClelland, lend themselves more naturally for network modeling). He argued that modeling RT data requires complex assumptions about criteria which can be both extraneous to the theory and difficult to check
1 . Here we present a framework adhering to the GRAIN principles, within which assumptions concerning decision criteria are explicitly modeled, and tested against data from new experiments and previously published studies.The second reason for the multiple read-out and variable criteria hypotheses was unification. The model allows us to give an integrative account of seemingly contradictory results in the literature concerning the facilitatory vs. inhibitory effects of orthographic neighborhoods, and the interactivity or additivity of word frequency and nonword lexicality with these neighborhood effects. The multiple read-out hypothesis allows the model to account for cross-task differences in word frequency and orthographic neighborhood effects, and also to simulate effects of frequency blocking manipulations that have proved to be a major obstacle for other models of visual word recognition.
TESTS OF THE MODEL
The section dealing with model testing is structured into two parts. In Part I, we present a series of new experiments designed to test the basic assumptions of our model (lexical inhibition, multiple read-out, and variable criterion hypotheses). These experiments examine the effects of orthographic neighborhood and word frequency on word stimuli in the perceptual identification task, and on word and nonword stimuli in the lexical decision task. In Experiment 1 a-d, neighborhood density and neighborhood frequency effects on word stimuli are studied while manipulating factors hypothesized to cause variations in the response criteria implemented in the model. In Experiment 2, we test for effects of the number and the frequency of word neighbors on performance to nonword stimuli in the lexical decision task. The multiple read-out model predicts effects of both of these factors. Finally, Experiment 3 contrasts word frequency and neighborhood frequency effects in a lexical decision and a perceptual identification task.
In Part II, we provide a series of simulation studies using stimuli available from previously published experiments. We demonstrate how the model helps resolve a number of inconsistencies in the experimental literature with respect to effects of orthographic neighborhoods, frequency blocking, and nonword lexicality on lexical decision performance, and word frequency effects in data-limited paradigms. Simulation Study 1 examines the interaction between word frequency, neighborhood density, and nonword lexicality. Simulation Study 2 investigates the additivity vs. interactivity of word frequency and neighborhood frequency in a lexical decision and a progressive demasking task. Simulation Study 3 examines a series of experiments reported by Sears et al. (1995) that failed to observe inhibitory effects of neighborhood frequency in the lexical decision task. Simulation Study 4 provides a further analysis of nonword lexicality effects on performance to word stimuli in the lexical decision task, and demonstrates that with the same strategic adjustments the model can also handle the effects of frequency blocking. These simulation studies focus largely on SATO phenomena and thus provide further independent tests of assumptions concerning the strategic adjustment of the ∑ and T criteria of the multiple read-out model. Finally, Simulation Study 5 examines the reported absence of word frequency effects with forced-choice, data-limited procedures (Paap & Johansen, 1994).
PART I: AN INVESTIGATION OF ORTHOGRAPHIC NEIGHBORHOOD AND WORD FREQUENCY EFFECTS IN LEXICAL DECISION AND PERCEPTUAL IDENTIFICATION
EXPERIMENT 1: Orthographic Neighborhood Effects in Low Frequency Words.
Previous research on the effects of neighborhood frequency (defined in terms of the relative frequency of the target word and its orthographic neighbors) has consistently shown inhibitory effects of this variable in the lexical decision task (Grainger, 1990; Grainger & Segui, 1990; Grainger et al., 1989; 1992; Marslen-Wilson, 1990; Pugh, Rexer, Peter, & Katz, 1994). Thus, words that are orthographically similar to a more frequently occurring word are generally harder to recognize than words that have no such higher frequency neighbors (but see Sears et al., 1995, for contradictory data). On the other hand, prior research on neighborhood density effects in lexical decision has generally shown facilitation if anything (Andrews, 1989; 1992; Sears et al., 1995). That is, increasing the number of orthographic neighbors of word stimuli facilitates recognition, but generally only for low-frequency stimuli.
In the following experiments, in one manipulation the number of high-frequency neighbors of low-frequency word stimuli was increased, while keeping overall neighborhood density constant. In another manipulation, neighborhood density was increased, while holding number of high-frequency neighbors constant. Four different sub-experiments using the same word stimuli allowed us to examine task, nonword context, and instructional influences on the neighborhood effects under study. Experiments 1A and 1B compare performance in the lexical decision task to performance in the progressive demasking paradigm (Grainger & Segui, 1990). This cross-task comparison is designed to distinguish task-specific and task-independent processes in visual word recognition (Jacobs, 1994; Jacobs & Grainger, 1994). In the multiple read-out model two of the decision criteria (∑ and T) are hypothesized to be specific to the lexical decision task. As argued in the introduction, by removing these task-specific components of the model we should be able to capture cross-task variations in performance. In Experiment 1C we used a different set of nonword stimuli, with lower average
s values (as computed by the model) than in Experiment 1B. Finally, in Experiment 1D the word and nonword stimuli of Experiment 1B were tested with instructions encouraging participants to give a preference to speed over accuracy in the lexical decision task. The comparison of Experiments 1B, 1C and 1D therefore corresponds to an ideal strategy manipulation in that the target stimuli and the presentation conditions remained unchanged (Stone & Van Orden, 1993).
Table 1. Qualitative predictions concerning the occurrence of inhibitory effects of neighborhood frequency (NF), facilitatory effects of neighborhood density (ND), and strategic variations in these effects as a function of the use made of the three processes assumed by the model (M,
S, and T). Y/N refers to the presence/absence of the different criteria and +/- represent high or low settings of the two strategically variable criteria (∑ and T). X, x, and o refer to predicted effect sizes (large, small, absent).M ∑ T NF ND
Progressive demasking task Y N N X o
(Experiment 1A)
Lexical decision with difficult nonwords Y Y+ Y+ X x (Experiment 1B)
Lexical decision with easy nonwords Y Y- Y+ x X
(Experiment 1C)
Lexical decision with speed stress Y Y- Y- x X (Experiment 1D)
Table 1 summarizes the experimental conditions used in Experiments 1 a - d and gives the qualitative predictions of the model outlined in Figure 1. It is important to note that these qualitative predictions are independent of the actual implementation of the model and the resulting quantitative predictions. The model predicts the presence of an inhibitory effect of neighborhood frequency for the conditions tested in Experiment 1A. It also predicts the absence of a facilitatory effect of neighborhood density, because the latter is assumed to result from the use of the ∑ and T criteria. By hypothesis, these criteria are not operational in the perceptual identification task. We hypothesize a high setting of both the ∑ and T criteria for the lexical decision task of Experiment 1B, which includes very word-like nonwords. Thus, inhibitory effects of neighborhood frequency, due to the frequent use of the M criterion, and weak effects of neighborhood density, due to the occasional use of the ∑ criterion, are predicted. The model predicts that using less word-like nonwords (Experiment 1C) should produce clear facilitatory effects of neighborhood density, due to the increased use of the lowered ∑ criterion. The model also predicts reduced effects of neighborhood frequency in Experiment 1C due to less involvement of the M criterion. Finally, despite the use of very word-like nonwords, the speed-stress instruction used in the lexical decision task of Experiment 1D should allow lower settings of both the ∑ and T criteria. This should produce a clear facilitatory effect of neighborhood density and a reduced effect of neighborhood frequency.
GENERAL METHOD
Design and stimuli. Four sets of 15 low-frequency 5-letter French words were selected. These words differed in terms of number of orthographic neighbors (neighborhood density) and the number of those neighbors that are more frequent than the word itself (number of high-frequency neighbors). The different categories of stimuli were controlled for printed frequency and positional bigram frequency (Imbs, 1971). The average number of neighbors, number of high-frequency neighbors, average printed frequency, and average bigram frequency of each category are given in Table 2. The critical comparisons relative to effects of neighborhood density and neighborhood frequency are the following: category 1 vs. 2, effect of the presence of one high-frequency neighbor; category 2 vs. 3, effect of neighborhood density; category 3 vs. 4, effect of number of high-frequency neighbors.
Participants. One hundred and twenty psychology students from René Descartes University participated in the experiment for course credit. All were native speakers of French with normal or corrected-to-normal vision. There were thirty participants in each sub-experiment.
Table 2. Average printed frequency (Freq), number of orthographic neighbors (N), number of high-frequency neighbors (NHF), and average positional bigram frequencies (BFreq) of the 4 categories of word stimuli used in Experiment 1. The frequencies are expressed as number of occurrences per million (Imbs, 1971).
STIMULUS CATEGORIES
C1 C2 C3 C4
Freq 15 14 18 14
N 1.47 1.73 5.80 6.53
NHF 0 1.0 1.0 4.13
BFreq 1872 1941 1993 2178
EXPERIMENT 1A: Progressive Demasking Task
METHOD
Design, stimuli, and participants. See General Method.
Procedure. Word stimuli were presented in alternation with a pattern mask. Each presentation cycle was composed of a given stimulus word followed immediately by a pattern mask of 5 hash marks. On each successive cycle the presentation of the stimulus was increased by 14 ms and the presentation of the mask decreased by 14 ms. The total duration of each cycle remained constant at 300 ms. Each trial consisted of a succession of cycles where stimulus presentation increased and mask presentation decreased. On the first cycle of each trial, stimuli were presented for 14 ms and the mask for 286 ms. On the second cycle, stimuli were presented for 28 ms and the mask for 272 ms etc. There was no interval between cycles. This succession of cycles continued until the participant pressed a response key on the computer key-board to indicate that he or she had recognized the stimulus word. Response latencies were measured from the beginning of the first cycle until the participant's response. Participants were instructed to focus their attention on the center of the visual display and to press the response key with the forefinger of their preferred hand as soon as they had recognized a word. They were instructed to type in the identified word using the key-board of the computer. Pressing the return key then initiated the following trial. Participants were asked to carefully check that they had correctly typed the word they thought had been presented before initiating the following trial.
RESULTS
Mean RTs for correct responses are given in Figure 4 (upper panel). The RT and error data were submitted to an analysis of variance. Outliers were removed before analysis using a 3000 ms cutoff (0.8% of the data eliminated). There was a significant main effect of neighborhood category in the RT data (F(3,87)=11.4, p< .001). Comparing RTs in the first two categories, we observed a significant inhibitory effect of the presence of one high-frequency neighbor (F(1,29)=4.55, p<.05). Increasing the number of neighbors of words with one high-frequency neighbor (category 2 vs. 3) produced no effect on RTs (F < 1). Increasing the number of high-frequency neighbors while keeping number of neighbors constant (category 3 vs. 4) produced a significant increase in RTs (F(1,29)=10.96, p<.01). None of these effects were significant in an analysis of the error data. The error rates for each stimulus category were 1.4%, 2.7%, 3.4%, 2.3%, respectively.
EXPERIMENT 1B: Lexical Decision With High
s NonwordsDesign and Stimuli. The same word stimuli as in Experiment 1A were used here. Sixty orthographically legal, pronounceable nonword stimuli were added for the purposes of the lexical decision task. Otherwise the design was identical to Experiment 1A. The nonword stimuli of Experiment 1B all had relatively high
s values as calculated by the model (the average s value after 7 cycles was 0.25).Procedure. Targets were presented at the center of a computer screen and remained in view until participants responded by pressing one of two response keys. Each target was preceded by a central fixation point which remained on the screen for 500 ms and was followed by a 500 ms interval before target presentation. Participants were instructed to fixate the center of the display and respond as rapidly and as accurately as possible whether the target string was a French word or not. They responded positively with the index finger of their preferred hand and negatively with the other hand.
Participants. See General Method.
RESULTS
Mean RTs for correct responses (Figure 4, lower panel) and percentage of errors (Figure 6, upper panel) for the word stimuli were submitted to an analysis of variance. Outliers were removed before analysis using a 1500 ms cutoff (0.3% of the data eliminated). There was a significant main effect of Neighborhood Category in both the RT data (F(3,87)=9.94, p<.001) and the percent errors (F(3,87)=3.84, p<.05). However, the only planned comparison to reach significance was between categories one and two. We observed a significant inhibitory effect of the presence of one high-frequency neighbor (F(1,29)=34.65, p<.001) which is also reflected by a significant increase in error rate between these two categories (F(1,29)=5.94, p<.05).
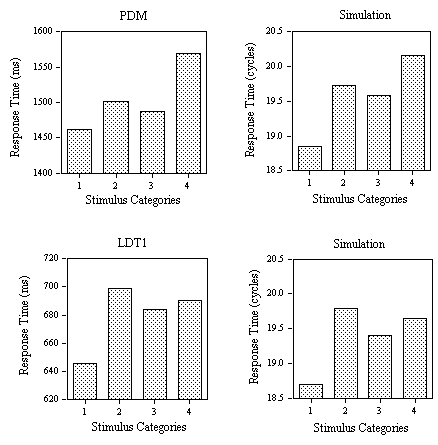
Figure 4. Obtained and predicted effects (Simulation) on response times to the different categories of low-frequency word stimuli (1: small N / no high-frequency neighbor; 2: small N / one high-frequency neighbor; 3: large N / one high-frequency neighbor; 4: large N / several high-frequency neighbors) tested with the progressive demasking (PDM) and lexical decision tasks (LDT1) in Experiments 1A and 1B. The nonword foils used in the lexical decision task had high average
s values.
EXPERIMENT 1C: Lexical Decision With Low
s Nonwords
In Experiment 1C the nonword stimuli of Experiment 1B were replaced with a new set of nonwords. These were orthographically regular and pronounceable nonwords with low
s values (the average s value after 7 cycles was 0.17). The model predicts that the presence of low s nonwords should enable participants to set a lower ∑ threshold without increasing false positive error rate. This should produce lower RTs overall. What is more important, the model predicts a different pattern of effects in these conditions (see Figure 5, upper panel). It should be noted that the nonword lexicality manipulation used in the present experiments differs from those used in other studies (e.g., Stone & Van Orden, 1993) in that nonword pronounceability and orthographic legality were not modified.METHOD
Design, Stimuli, and Procedure. Same as Experiment 1B except for the different nonword stimuli as noted above.
Participants. See General Method.
RESULTS
Mean RTs for correct responses (Figure 5, upper panel) and percentage of errors (Figure 6, middle panel) for the word stimuli were submitted to an analysis of variance. Outliers were removed before analysis using a 1500 ms cutoff (0.1% of the data eliminated). There was a significant main effect of Neighborhood Category in the RT data (F(3,87)=4.22, p<.01). Comparing RTs in the first two categories, we observed a significant inhibitory effect of the presence of one high-frequency neighbor (F(1,29)=10.12, p< .01). Increasing the number of neighbors of words with one high-frequency neighbor (category 2 vs. 3) produced a significant facilitatory effect (F(1,29)=5.40, p<.05). Increasing the number of high-frequency neighbors while maintaining number of neighbors constant had no effect (F < 1). None of these effects were significant in an analysis of the error data.
EXPERIMENT 1D: Lexical Decision With High
s Nonwords and Speed InstructionsThe multiple read-out model predicts that the type of criterion shift that is caused by a decrease in nonword lexicality (as illustrated in the observed differences in Experiments 1B and 1C) should also be produced by stressing speed over accuracy in the instructions given to participants. Experiment 1D tests this particular prediction of the model.
METHOD
Design, Stimuli, and Procedure. Same as Experiment 1B except for the instructions given to participants that stressed speed over and above accuracy.
Participants. See General Method.
RESULTS
Mean RTs for correct responses (Figure 5, lower panel) and percentage of errors (Figure 6, lower panel) for the word stimuli were submitted to an analysis of variance. Outliers were removed before analysis using a 1500 ms cutoff (0.12% of the data eliminated). The main effect of neighborhood category was not significant in the RT data (F(3,87)=2.4, p<.10). There was a significant inhibitory effect of the presence of a single high-frequency neighbor (category 1 vs. 2, F(1,29)=4.45, p<.05). Increasing the number of neighbors of words with one high-frequency neighbor (category 2 vs. 3) produced a significant facilitatory effect (F(1,29)=4.91, p<.05). Increasing the number of high-frequency neighbors while maintaining number of neighbors constant had no significant effect (F < 1). In an analysis of the error data there was a significant main effect of neighborhood category (F(3,87)=7.34, p<.001) and significant effects of both neighborhood frequency (F(1,29)=20.06, p<.001) and neighborhood density (F(1,29)=15.13, p<.001). Increasing the number of high-frequency neighbors did not significantly affect percent errors (F(1,29)=3.9, p<.10).
SIMULATION
The simulation procedure was the same as in Jacobs and Grainger (1992) and further details of the present simulation are given in the Appendix. In the simulations presented in Figures 4, 5, and 6, the response criteria were modified in the following ways in order to reproduce the variations in the pattern of effects observed across Experiments 1A to D: 1) In the first simulation only the M threshold was used, whereas in the other three simulations the ∑ and T thresholds were also included. In the progressive demasking task (and other perceptual identification tasks) participants have to isolate a single word for response. In the multiple read-out model, this can only be achieved via the M decision criterion. Since errors did not significantly vary across stimulus categories in Experiment 1A, in order to simplify matters the corresponding simulation was error free (i.e., no noise was introduced in order to simulate identification errors in the progressive demasking paradigm, see Ziegler, Rey, & Jacobs, submitted). 2) In order to simulate the effects of nonword lexicality (
s values) in the lexical decision task (Experiments 1B and 1C), the ∑ decision criterion was lowered in the third simulation. Here we test the hypothesis that participants can modify this decision criterion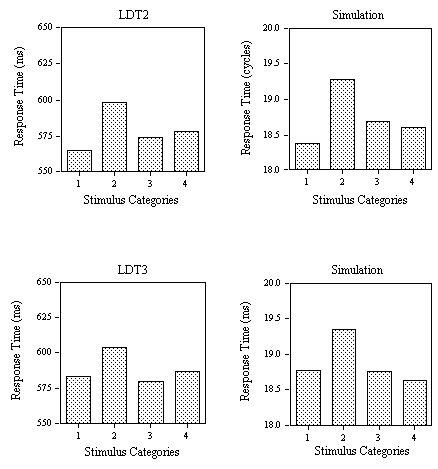
Figure 5. Obtained and predicted effects (Simulation) on response times to the different categories of low-frequency word stimuli (1: small N / no high-frequency neighbor; 2: small N / one high-frequency neighbor; 3: large N / one high-frequency neighbor; 4: large N / several high-frequency neighbors) in Experiment 1C using nonword foils with low average
s values (LDT2) and Experiment 1D using nonword foils with high average s values and speed instructions (LDT3).
during the course of an experiment as a function of the distribution of word and nonword
s values. More specifically, it is hypothesized that the lower the s values of nonword stimuli in the experiment, the lower the average value of the ∑ threshold that will be adopted. This will result in faster positive RTs without an increase in error rate. 3) In order to simulate the way speed instructions affected performance in Experiment 1D, both the ∑ and the T criteria were lowered. This will produce faster positive and negative RTs, and an increase in both false positive and false negative errors. The values of the ∑ criterion adopted for this simulation were identical to those used to simulate Experiment 1C.The criterion adjustments used in the present simulations can be summarized as follows (see also Table 1). Experiment 1A: M criterion only; Experiment 1B: M, ∑+, T+; Experiment 1C: M, ∑-, T+; Experiment 1D: M, ∑-, T-; where +/- refers to high or low criterion settings. It should be noted that all other aspects of the model remained unchanged in the different simulations presented here. The details of the specific criterion values adopted in each simulation are given in the Appendix.
DISCUSSION
The results of Experiment 1 along with the corresponding simulation results are given in Figures 4, 5, and 6. Since these experiments were designed to examine the influence of type of task, nonword lexicality, and task instructions on the effects of neighborhood frequency and neighborhood density in visual word recognition, each of these points will be dealt with in turn.
Task differences.
Comparing the progressive demasking results with the first lexical decision experiment (PDM vs. LDT1) given in Figure 4, it is clear that the model captures the inhibitory effect of a single high-frequency neighbor (category 1 vs. 2) that occurs in both experiments. Secondly, the model correctly predicts an inhibitory effect of number of high-frequency neighbors (category 3 vs. 4) which is greatly reduced (compared to the size of the previous effect) in the lexical decision task but not in the progressive demasking task. Within the theoretical framework developed in the present paper, we argue that positive responses in the progressive demasking and lexical decision tasks are generated using the M criterion. However, unlike the progressive demasking task, performance in the lexical decision task can be modified by the intervention of two additional decision criteria (∑ and T). Adding these two decision criteria allows the model to capture the main differences in the pattern of effects observed in Experiments 1A and 1B, as noted above.

Figure 6. Obtained and predicted effects (Simulation) on false negative error rates to the different categories of low-frequency word stimuli (1: small N / no high-frequency neighbor; 2: small N / one high-frequency neighbor; 3: large N / one high-frequency neighbor; 4: large N / several high-frequency neighbors) in Experiment 1B (LDT1: nonwords with high average
s values), Experiment 1C (LDT2: nonwords with low average s values), and Experiment 1D (LDT3: nonwords with high average s values and speed instructions).
Effects of nonword lexicality.
Comparing the two lexical decision experiments that used nonwords with different
s values (LDT1 vs. LDT2), it was predicted that the presence of nonwords with low s values would increase the use made of the ∑ decision criteria. In this way, the model captures the decrease in RT from Experiment 1B to 1C (for approximately equal error rates). More interestingly, the model captures the variations in effect sizes across Experiments 3B and 3C. Thus, neighborhood density effects (category 2 vs. 3) are only robust when low s nonwords are used (cf. Andrews, 1989). Although neighborhood frequency effects (category 1 vs. 2) were robust in both experiments, the model correctly predicts that these are slightly smaller in Experiment 1C.Effects of task demands.
In Experiment 1D, participants were instructed to perform the lexical decision task as rapidly as possible even if this increased their error rate. Since the stimuli were identical to those used in Experiment 1B, a comparison of the results of these two experiments reveals the effects of stressing speed relative to accuracy on performance in the lexical decision task. The results are strikingly similar to the effect of reducing nonword lexicality. The main difference is that the decrease in average RT is now accompanied by a large increase in error rate. By lowering the average value of the ∑ and T decision criteria, the multiple read-out model captures the decrease in both positive and negative RTs accompanied by an increase in false positive and negative error rate. Moreover, the model correctly predicts that facilitatory effects of neighborhood density increase in size when participants are instructed to give a preference to speed over accuracy in the lexical decision task.
Figure 7 shows variations in the size of neighborhood density and neighborhood frequency effects across the three lexical decision experiments. The net inhibitory effects of neighborhood frequency are calculated by subtracting mean RT in category 1 from mean RT in category 2. The net facilitatory effects of neighborhood density are calculated by subtracting mean RT in category 3 from mean RT in category 2. This figure shows that the multiple read-out model accurately captures the variation in neighborhood frequency and neighborhood density effects as a function of nonword lexicality and task demands.
As an overall evaluation of the model's capacity to predict RT differences across conditions in Experiment 1, we correlated mean RT with mean number of cycles separately for each sub-experiment. In the progressive demasking task of Experiment 1A this involved the means for the four neighborhood categories. In the lexical decision experiments mean nonword RT, mean error RT to word stimuli, and mean error RT to nonword stimuli provided three additional means. This gave the following results: Experiment 1A (N=4), r = .91; Experiment 1B (N=7), r = .97; Experiment 1C (N=7), r = .97; Experiment 1D (N=7), r = .93
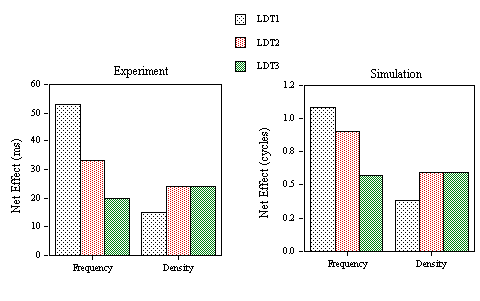
Figure 7. Net predicted and obtained effects of neighborhood frequency (RT in category 2 - RT in category 1) and neighborhood density (RT in category 2 - RT in category 3) in Experiment 1B (LDT1: nonwords with high average
s values), Experiment 1C (LDT2: nonwords with low average s values), and Experiment 1D (LDT3: nonwords with high average s values and speed instructions).
Finally, an analysis of the RT distributions in the lexical decision experiments (Experiments 1B, 1C, and 1D) and the corresponding simulations was performed (see Jacobs & Grainger, 1992, for a detailed description of the method). The correct RT distributions are given for 10% quantiles. Incorrect RT distributions are given for 20% quantiles, simply because of the much smaller number of data points in this case. Stochastics are introduced in the present model in the form of response criteria that vary from trial to trial following a normal distribution with a given mean and standard deviation. This allows the collection of one simulation data point for every experimental data point. Therefore, the same analysis can be applied to the simulation and the experimental data. Simulation data (in cycles) were first transformed into RT using the scalar of the appropriate regression equation given above, and adjusting the intercept to give identical starting points for the experimental and simulation distributions. The results of this analysis, given in Figures 8-10, show that the model does reasonably well in capturing variations in correct and incorrect positive and negative RTs in the lexical decision task.
The major problem with the simulated distributions is that they underestimate the positive skew of the experimental distributions. Clearly, this could be due to the presence of a small number of large RTs in a typical lexical decision experiment (not treated as outliers by the cutoffs applied here) that may be the result of mechanisms external to the normal lexical decision process.
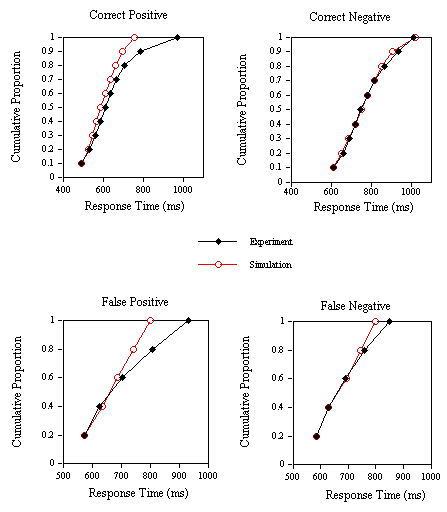
Figure 8. Group cumulative distribution functions for the experimental and simulation correct positive, correct negative, false positive and false negative response times in Experiment 1B (nonwords with high average
s values).
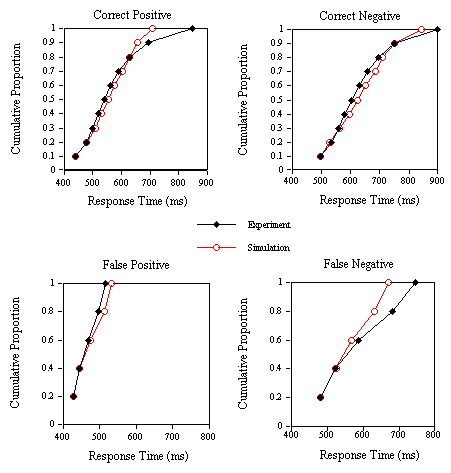
Figure 9. Group cumulative distribution functions for the experimental and simulation correct positive, correct negative, false positive and false negative response times in Experiment 1C (nonwords with low average
s values).
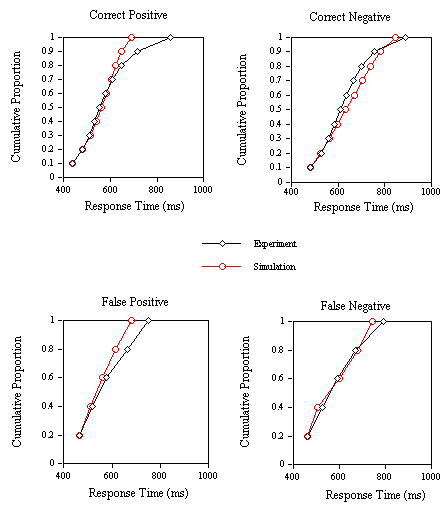
Figure 10. Group cumulative distribution functions for the experimental and simulation correct positive, correct negative, false positive and false negative response times in Experiment 1D (speed instructions).
EXPERIMENT 2: Orthographic Neighborhood Effects on Nonword Stimuli in Lexical Decision.
Since our model has the particularity that it can make qualitative and quantitative predictions concerning RTs and errors to nonword stimuli in the lexical decision task, Experiment 2 examines neighborhood effects with nonword stimuli. Contrary to the empirical evidence concerning effects of orthographic neighbors on positive latencies in the lexical decision task, there is much more coherence in the literature as far as effects on negative latencies are concerned. Andrews (1989) and Coltheart et al. (1977) have reported that nonword stimuli with large neighborhoods take longer to reject than nonword stimuli with small neighborhoods. More recently, however, Andrews (1992) reported the absence of an effect of neighborhood size on nonword decision latencies when the stimuli are carefully controlled for bigram frequency. Strangely enough, a subsequent experiment in the same series, yielded a null effect of bigram frequency on nonword decision latencies. This latter result therefore implies that it was not the control for bigram frequency that cancelled the effects of neighborhood density on responses to nonword stimuli. It is therefore likely that some other characteristic of the nonword stimuli used by Andrews (1992) be responsible for the obtained null effect. In Experiment 2 we test the hypothesis, inherent in the multiple read-out model, that the printed frequencies of the word neighbors of nonword stimuli will affect lexical decisions to these stimuli.
EXPERIMENT 2A
METHOD
Design and stimuli. Forty 4-letter orthographically legal and pronounceable nonword strings were generated with respect to two dimensions: 1) The number of French words that share all but one letter in the same position (neighborhood density or N; half of the nonwords had an average N value of 2.3; the remaining half had an average N value of 7.7), and 2) the number of French words that share all but one letter in the same position and that have a printed frequency greater than 100 occurrences per million (Imbs, 1971). The latter factor is referred to as Neighborhood Frequency and the nonword stimuli had either no word neighbors with a printed frequency greater than 100 (in which case the maximum frequency was 50 occurrences per million), or at least one such word neighbor (average=2.7). These two factors were crossed in a 2X2 factorial design. Forty French words, all four letter long (with an average printed frequency of 68 occurrences per million), were also included in the stimulus list for the purposes of the lexical decision task.
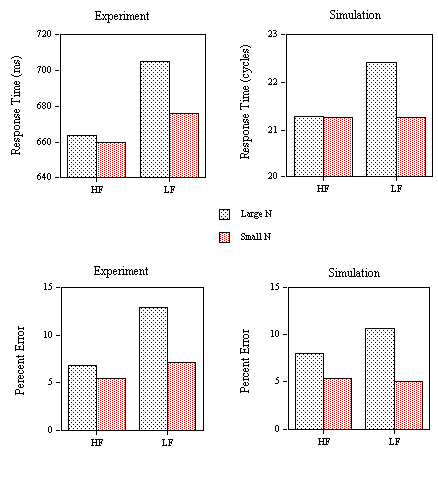
Figure 11. Obtained effects (Experiment) and predicted effects (Simulation) of neighborhood size (large N or small N) and neighborhood frequency (at least one high-frequency neighbor or all low frequency) on response times and false positive errors to the nonword stimuli of Experiment 2A.
Procedure. Standard lexical decision procedure was used here with participants instructed to respond as rapidly and as accurately as possible whether a string of letters formed a French word or not. Each trial began with a central fixation point which remained on the screen for 500 ms, followed 500 ms later by the target string in upper case letters. Targets remained on the screen until participants responded.
Participants. Twenty-five students of psychology from René Descartes University took part in the experiment for course credit. All were native speakers of French with normal or corrected-to-normal vision.
RESULTS
Mean RTs (applying a 2000 ms cutoff eliminating 0.27% of the data) and percent errors for the different categories of nonword stimuli are given in Figure 11. An analysis of variance on the RT data showed a facilitatory effect of neighborhood frequency (F(1,24)=20.49, p< .001) and a non-significant inhibitory effect of neighborhood density (F(1,24)=3.8, p<.10). Although neighborhood density did not significantly interact with neighborhood frequency (F(1,24)=2.62, p >.10), the inhibitory effects of density only appeared when all neighbors were low-frequency (F(1,24)=5.32, p<.05) and not when at least one of the neighbors was high-frequency (F < 1).
An analysis of variance on the percent error data showed significant main effects of both neighborhood density (F(1,24)=6.25, p<.05) and neighborhood frequency (F(1,24)=6.6, p< .05). The interaction was not significant, but as in the RT analysis, the inhibitory effects of neighborhood density only appeared when all neighbors were low-frequency (F(1,24)=4.67, p<.05). Average correct lexical decision time to the word stimuli was 606 ms (with RTs less than 2000 ms representing 0.2% of the data eliminated) and the average number of false negative errors (miss rate) was 7.7% with average miss RT at 658 ms.
SIMULATION
The mean number of cycles to reach the T criterion and mean error rate for the nonwords (i.e., the proportion of trials in which the M or ∑ criteria were reached before the T criterion) in each condition of Experiment 2A are given in Figure 11 along with the corresponding mean RTs and error rate from the experiment. As can be seen in Figure 11, the model very accurately predicts the variations in mean RT and percent error across the four types of nonwords tested in Experiment 2A. More precisely, the model correctly predicts that inhibitory effects of neighborhood density only occur when the neighbors of the nonword stimuli are all relatively low-frequency words. The simulated mean RT for word stimuli is 18.97 cycles with an error rate of 7.75% and an average miss RT of 20.06 cycles. As an overall evaluation of the model's capacity to predict the variations in RT across conditions in Experiment 2A, we correlated mean RT with mean number of cycles for seven conditions corresponding to the four nonword conditions, mean word RT, mean error RT to word stimuli, and mean error RT to nonword stimuli (r = .95). A comparison of the error rates obtained in experimentation and those predicted by the model (N = 5) yielded a correlation of 0.86. The multiple read-out model accurately predicts variations in mean correct negative RT as a function of the neighborhood characteristics of the nonword stimuli. It also correctly predicts the relation between mean correct positive and negative RTs, and incorrect positive and negative RTs. Moreover, the simulated pattern of errors closely reflects the observed values.
The grouped cumulative distribution functions (CDFs) for correct and incorrect positive and negative RTs are given in Figure 12. These distribution analyses show that the model not only captures variations in mean RT in an experiment, but also how these RTs vary around the mean value. The model's ability to give a reasonably accurate description of the shape of these different RT distributions is all the more impressive in that the four experimental distributions have very different shapes themselves.
DISCUSSION
The results of Experiment 2A show that the printed frequency of the word neighbors of nonword stimuli significantly affects both RT and accuracy to such stimuli in a lexical decision task. Such a facilitatory nonword neighborhood frequency effect has previously been reported by Den Heyer et al. (1988). The fact that the inhibitory effects of neighborhood density in nonword stimuli disappear when at least one of the neighbors is a high-frequency word, provides one possible explanation for prior discrepancies with respect to the effects of this variable (Andrews, 1992).
The simulation results show that our lexical decision model accurately captures the pattern of means observed in experimentation for both the RT and the error data. At present, no other mathematical or algorithmic model of visual word recognition is capable of simulating both the mean and distribution of RTs and percent errors. Moreover, the model successfully captures the mean and distribution of error RTs to word (false negative) and nonword stimuli (false positive).
The pattern of mean RTs observed in Experiment 2 is not readily accommodated by serial search and verification models of the lexical decision task. This class of model predicts that increasing the number of high-frequency neighbors ought to have a negative effect on RT additive with the effects of neighborhood density. In search models, increasing the frequency of the word neighbors of nonword stimuli should increase the likelihood that these neighbors be included in the search/verification process.
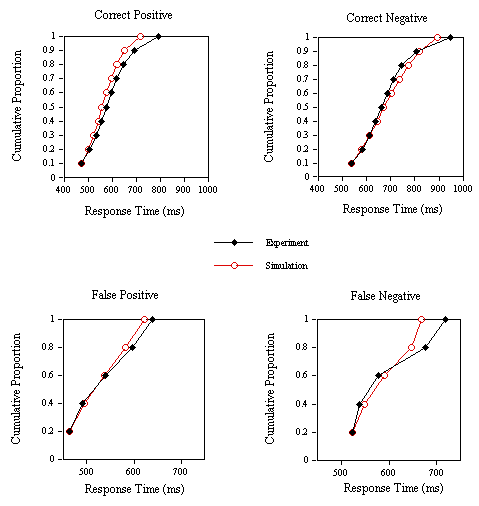
Figure 12. Group cumulative distribution functions for the experimental and simulation correct positive, correct negative, false positive and false negative response times in Experiment 2A.
Within the present theoretical framework, nonword RTs in the lexical decision task were correctly predicted to depend on the total lexical activation generated by a nonword stimulus in early phases of processing. Since these
s values will generally correlate with the N values of the nonword stimuli, the model correctly predicts inhibitory effects of neighborhood density on nonword latencies (Coltheart et al., 1977; Jacobs & Grainger, 1992). The present results suggest, however, that the inhibitory effects of neighborhood density on nonword decision latencies are influenced by the printed frequencies of the word neighbors. When at least one of the neighbors has a high printed frequency (greater than 100 occurrences per million), then the inhibitory effects are greatly diminished. A closer examination of the s values of a large set of 4-letter nonwords indicated that increasing the number of high-frequency neighbors in large N nonwords should have a facilitatory effect on performance to these stimuli. In other words, it is not simply the presence or absence of at least one frequent word neighbor that should be critical (as was manipulated in Experiment 2A) but the total number of high-frequency word neighbors relative to the total number of neighbors.Experiment 2B investigates this specific prediction of the multiple read-out model with respect to the facilitatory effects of neighborhood frequency on lexical decision latencies to nonword stimuli. Moreover, since the observation of a facilitatory effect of neighborhood frequency in Experiment 2A is a new finding that merits further investigation, Experiment 2B tests whether this facilitation is a categorical effect due to the presence of at least one high-frequency neighbor or is related to the total number of high-frequency neighbors of nonword stimuli.
EXPERIMENT 2B
METHOD
Design and Stimuli. Three categories of 4-letter orthographically legal and pronounceable nonwords were selected on the basis of the number of high-frequency word neighbors. The nonword stimuli of category 1 had no high-frequency neighbors (all less than 50 occurrences per million), those of category 2 all had one high-frequency neighbor (greater than 100 occurrences per million), and the stimuli of category 3 all had at least 3 high-frequency neighbors (average=3.8). Otherwise, the three categories were matched as closely as possible for total number of neighbors (N = 8.6, 7.7, and 8.2, respectively). These three categories did necessarily differ in terms of positional bigram frequency. However, since Andrews (1992) has reported a null effect of bigram frequency on nonword lexical decision latencies when neighborhood density is controlled, we can safely attribute any differences observed in the present experiment to effects of neighborhood frequency.
Procedure. This was identical to Experiment 2A.
Participants. Twenty-five students of psychology at René Descartes University received course credit for participating in the experiment. All were native speakers of French with normal or corrected-to-normal vision.

Figure 13. Obtained effects (Experiment) and predicted effects (Simulation) on response times and false positive error rates in the different categories of nonword stimuli (no high-frequency neighbor, one high-frequency neighbor, several high-frequency neighbors) tested in Experiment 2B .
RESULTS
Mean RT (applying a 2000 ms cutoff eliminating 0.38% of the data) and percent error to the three categories of nonword stimuli are given in Figure 13. An analysis of variance performed on these data showed significant facilitatory effects of number of high-frequency neighbors (0, 1, or > 2) in both the RT (F(2,48)=5.74, p<.01) and the percent error analysis (F(2,48)=6.92, p<.01). Planned comparisons indicated that the slight increase in RT from category 1 to category 2 was not significant (F<1), whereas the decrease in RT from category 2 to category 3 was significant (F(1,24)=10.12, p<.01). In an analysis of the percent errors, neither of these effects were significant. The average correct RT to word stimuli was 629 ms, with 7.3% false negative errors. The average false negative RT was 658 ms, and the average false positive RT 600 ms.
SIMULATION
The mean number of cycles to reach the T criterion and percent error for the three categories of nonwords tested in Experiment 2B are given in Figure 13. The model captures the main effect of neighborhood frequency on nonword stimuli in both the RTs and percent errors. Mean RT to the word stimuli was 18.67 cycles and percent error was 6.37% with average miss RT at 21.24 cycles. A correlation between mean RT and mean number of cycles for the three nonword conditions plus correct word RT, miss RT, and false alarm RT yielded a coefficient of .97 (N = 6). The correlation between observed and predicted percent errors was .97 (N = 4).
The experimental and simulation CDFs presented in Figure 14 show that the model can accurately predict the distributional characteristics of both correct and incorrect positive and negative RTs in the lexical decision task.
DISCUSSION
The main result of Experiment 2B indicates that number of high-frequency word neighbors significantly affects RTs to nonword stimuli in the lexical decision task. Contrary to the inhibitory effects of total number of orthographic neighbors (Andrews, 1989; Coltheart et al., 1977), increasing the number of frequent neighbors facilitates responses to nonword stimuli when total number of neighbors is held constant. This new finding should constrain future models of lexical decision and word recognition. More precisely, this result directly contradicts frequency-ordered search and verification models which clearly predict inhibitory effects of neighborhood frequency on nonword RTs. The multiple read-out model correctly predicted these facilitatory effects of number of high-frequency neighbors on performance to nonword stimuli in a lexical decision task. Due to the dynamics of lexical inhibition in the model, increasing the number of high-frequency word neighbors of nonword stimuli actually results in a decrease in overall lexical activity in early stages of processing. In this way, a lower T criterion can be set for negative responding, and faster RTs result. The lexical inhibition hypothesis is critical for predicting such an effect within the framework of the multiple read-out model. Without mutual inhibition between word units, total lexical activity would systematically increase as the frequency of the word neighbors of nonword stimuli increases, and inhibitory effects would therefore be predicted.
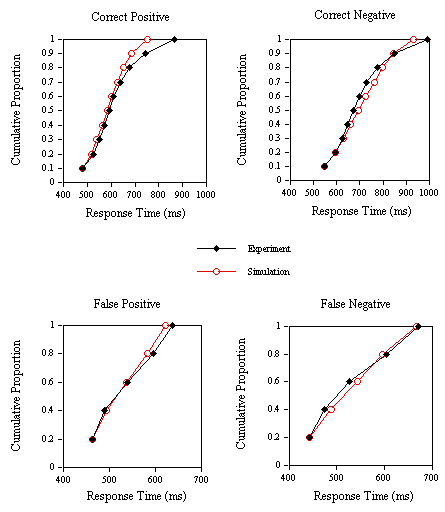
Figure 14. Group cumulative distribution functions for the experimental and simulation correct positive, correct negative, false positive and false negative response times in Experiment 2B.
Introducing stochastics in the form of variable response criteria, provided us with a simple means of capturing variations in percentage of errors as well as RTs in the lexical decision task. Grainger and Jacobs (1994) have provided a similar application of the principle of variable response criteria to predict forced choice accuracy in the Reicher paradigm. The distributional analyses of Experiments 1 and 2 join the previous analyses of Jacobs and Grainger (1992) in suggesting that this particular means of introducing stochastics in an interactive activation network provides a good description of the observed variability in human RT data. In Experiment 3, we examine whether this same mechanism can provide an accurate description of data obtained in a perceptual identification task.
EXPERIMENT 3: Word Frequency and Neighborhood Frequency effects in Perceptual Identification and Lexical Decision
Experiment 3 examines word frequency and neighborhood frequency effects in a perceptual identification and a lexical decision task. The variable criteria of the model successfully simulated the RT distributions observed in the lexical decision task. We suggest that the same variability set on the M criterion can also be successfully applied to simulate percent correct word identification in a perceptual identification task. In this task, a stimulus word is presented tachistoscopically with a forward and backward pattern mask. Stimulus exposure duration is adjusted so that participants correctly report the word stimulus only on a certain proportion of trials. In the multiple read-out model, correct word identification will arise if the maximum activation attained by a given word unit on a given trial is greater than the value of the M criterion. In the model, this is simulated by reducing feature-to-letter excitation by a constant amount (0.00095) on every cycle after a fixed number of cycles corresponding to the simulated stimulus exposure duration (5 cycles was the value used here). This simply provokes a gradual decrease in the growth of activation of letter and word units until a maximum value is reached and the values then decrease to resting level. Since the M criterion varies normally from trial-to-trial around a mean value, the maximum word unit activity will sometimes be greater and sometimes less than this criterion. According to this method of simulating the perceptual identification task, the backward mask does not immediately erase the activation levels of features that had been activated by the stimulus (as was the case in the original interactive activation model, McClelland & Rumelhart, 1981). Instead, feature-level activation decays more rapidly in the presence than in the absence of a pattern mask. In other words, the backward mask is thought to reduce the sustained activity of feature, letter, and word representations after stimulus offset.
EXPERIMENT 3A: Perceptual Identification
Design and stimuli. Eighty 5-letter French words of either high (average 260 per million) or low (average 13 per million) printed frequency were selected. These words all had a relatively small number of orthographic neighbors (average of 2.5) but differed in terms of whether one of these neighbors had a high printed frequency (average 508 occurrences per million) or not (all neighbors with a frequency less than 25 per million). Thus, word frequency (low or high) was crossed with neighborhood frequency (one high-frequency or none high frequency) in a 2X2 factorial design with 20 words per condition.
Procedure. Word stimuli were presented for two refresh cycles on a 50 Hz monitor (40 ms) preceded and followed by a pattern mask consisting of a row of 5 hash marks (#). The forward mask lasted for 500 ms and the backward mask remained on the screen until participants initiated the following trial. Participants were instructed to focus their attention on the center of the visual display and to type in any word they successfully identified using the key-board of the computer. Participants were not encouraged to guess when responding, but simply to report words that they had recognized. Pressing the return key after typing in the response initiated the following trial and participants were asked to carefully check that they had correctly typed the word they thought had been presented before initiating the following trial.
Participants. Thirty third-year psychology students from René Descartes University served as participants for course credit. All were native speakers of French with normal or corrected-to-normal vision.
RESULTS
Means of percent correct responses are given in Figure 15. These data were submitted to an analysis of variance. The analysis showed main effects of both Word Frequency (F(1,29)=33.28, p<.001) and Neighborhood Frequency (1,29)=7.42, p<.05) which significantly interacted (F(1,29)=6.12, p<.05). The 9% inhibitory effect of the presence of a high-frequency neighbor in low-frequency words was statistically reliable (F(1,29)=11.61, p<.01), whereas the 3% inhibition observed with the high-frequency targets was not significant (F(1,29)=1.59, p>.10). The effects of word frequency, on the other hand, were robust for both neighborhood categories.
SIMULATION
Only the M criterion set on word unit activity (with the same mean and standard deviation as in the previous simulations) was used to simulate performance in the perceptual identification task. After 5 processing cycles, the value of the feature-to-letter excitation parameter (0.005) was reduced by a constant value (0.00095) on each successive cycle. This resulted in the stimulus word reaching a maximum activation of approximately 0.68 (the value of the M criterion) after approximately 25 cycles of processing, followed by a gradual decrease in activation level toward its resting level value. All words tested in the experiment were presented to the model on 30 occasions and the percentage of trials on which the variable M criterion was reached was recorded. The means of the percent correct data for each experimental condition are given next to the experimental results in Figure 15. As is evident in this figure, the multiple read-out model provides an extremely accurate description of the effects of neighborhood frequency and word frequency in a perceptual identification task.
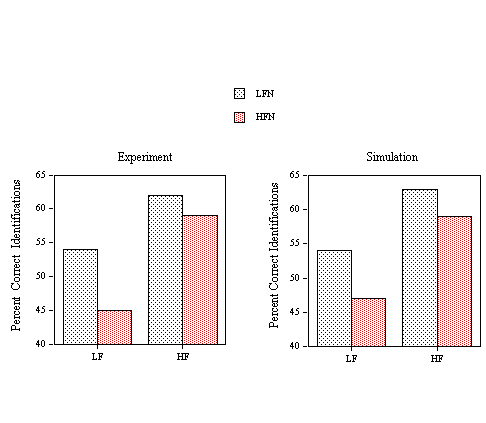
Figure 15. Obtained effects (Experiment) and predicted effects (Simulation) on percent correct identification of the high (HF) and low (LF) frequency words with (HFN) or without (LFN) a single high-frequency neighbor tested in Experiment 3A .
EXPERIMENT 3B: Lexical Decision
Design and Stimuli. The same eighty target words as in Experiment 3A were used again. Eighty orthographically legal, pronounceable nonword strings of five letters in length were constructed for the purposes of the lexical decision task. The nonwords used in Experiment 3B all generated very high summed activation values in the model (average
s(7)=0.35).Procedure. The same procedure was used as in Experiment 1B. Participants were instructed to respond as rapidly as possible while making as few errors as possible.
Participants. Thirty third-year psychology students from René Descartes University served as participants for course credit. All were native speakers of French with normal or corrected-to-normal vision. None of them had participated in the previous experiment.
RESULTS
Means of RTs for correct responses are given in Figure 16. The RT and error data were submitted to an analysis of variance. Outliers were removed before analysis using a 1500 ms cutoff (0.2% of the data). In the analysis of the RT data, there was a main effect of Word Frequency (F(1,29)=89.85, p<.001), no significant effect of Neighborhood Frequency (F < 1), and a significant interaction between these two factors (F(1,29)=14.13, p<.001). As can be seen from Figure 16, the presence of a high-frequency neighbor inhibited performance to the low-frequency targets, but facilitated performance to the high-frequency targets. The only significant effect in the error data was a main effect of Word Frequency (F(1,29)=17.21, p<.001).
SIMULATION
The values of the
S and T criteria adopted to simulate the lexical decision results of Experiment 3B were very similar to those used in the simulation of Experiment 1B (see Appendix). Only minor adjustments of these criterion settings were made as a function of the s values of the word and nonword stimuli used in this experiment. The means per experimental condition after 30 simulation runs are given next to the experimental means in Figure 16. As can be seen in this figure, the model correctly captures the interaction between word frequency and neighborhood frequency observed in Experiment 3B. This arises due to the fact that the high-frequency words with a high-frequency neighbor tended to have higher s values than words in the other experimental conditions. This implies that the ∑ criterion is generating fast positive responses mainly for this particular condition. Thus, the slight disadvantage with respect to high-frequency words with no high-frequency neighbor in the perceptual identification task, is transformed into a facilitatory effect in lexical decision.
Figure 16. Obtained effects (Experiment) and predicted effects (Simulation) on response times and false negative error rates to the high (HF) and low (LF) frequency words with (HFN) or without (LFN) a single high-frequency neighbor tested in Experiment 3B .
As in the simulations of Experiment 1, it was not sufficient for the model to capture the results concerning correct positive RTs and false negative errors, but with the same criterion settings it had also to provide a realistic estimate of correct negative RTs, false positive errors, and RTs to both types of error. In order to test this, the correlations between mean predicted and observed RT and error rate for these different conditions were calculated. The correlation between predicted and obtained error rate was .99 (N=5), while the correlation between predicted and obtained mean RT was .66 (N=7).
DISCUSSION
The results of Experiment 3 demonstrate strong inhibitory effects of a single high-frequency neighbor in a perceptual identification task, particularly for low-frequency target words. These inhibitory effects diminished in the lexical decision task and actually became facilitatory for the high-frequency target words. These facilitatory effects were correctly predicted by the model due to the higher
s values generated by high-frequency words with a high-frequency neighbor.The observed interaction between target word frequency and neighborhood frequency replicates the prior observation of such an interaction by Grainger and Segui (1990) in a progressive demasking experiment. Medium frequency words suffered less interference from high-frequency neighbors than did low-frequency target words. This interaction was not observed in lexical decision latencies to the same target words, but did appear in the false negative error rates. In part 2 of the present work (Simulation Study 2), we show how the multiple read-out model nicely accounts for the different patterns obtained in these different tasks.
DISCUSSION OF PART I
The experiments and simulations presented in Part I have provided an initial test of the multiple read-out model of lexical decision and word recognition. More precisely, the experiments were designed as specific tests of the lexical inhibition, multiple read-out, and variable criteria hypotheses implemented in the model.
Experiment 1 tested the combined use of the M and ∑ criteria for positive responses as a function of type of task (lexical decision vs. progressive demasking), nonword lexicality, and task demands. By modifying the relative use made of the ∑ and T decision criteria, the model successfully captures variations in neighborhood frequency and neighborhood density effects across the different sub-experiments. By independently varying the number of neighbors and the number of high-frequency neighbors of low-frequency word stimuli, it was shown that the presence of a single high-frequency neighbor exerted a consistent inhibitory effect on word recognition performance. In contrast, increasing the number of neighbors of word stimuli tended to produce facilitatory effects. In the multiple read-out model, inhibitory neighborhood frequency effects observed in the lexical decision task arise from variations in the time taken by word units to reach the non-modifiable M decision criterion. Facilitatory neighborhood density effects are mainly the result of the strategically modifiable ∑ decision criterion. However, the effects of neighborhood frequency are also influenced by variations in the use made of the ∑ decision criterion, since words with high-frequency neighbors tend to have higher
s values than words with no high-frequency neighbors. Lower levels of nonword lexicality and instructions stressing speed are two factors hypothesized to increase the use made of the ∑ decision criterion. Thus, the model correctly predicts that inhibitory effects of neighborhood frequency decrease as nonword lexicality decreases, and as speed is emphasized over accuracy, whereas the facilitatory effects of neighborhood density do just the opposite (see Figure 7).Experiment 2 investigated the effects of neighborhood size and frequency on performance to nonword stimuli in the lexical decision task. Although increasing the number of orthographic neighbors of nonword stimuli typically produces slower RTs and larger error rates (Coltheart et al., 1977; Andrews, 1989), the present experiments demonstrated that these neighborhood density effects are modulated by the printed frequencies of the word neighbors. In Experiment 2A, it was shown that when none of the neighbors of nonword stimuli had high printed frequencies (all less than 50 occurrences per million), then increasing neighborhood size produced the standard inhibitory effect. In contrast, no effect was observed when the neighbors had high printed frequencies. This experiment also showed a facilitatory effect of nonword neighborhood frequency, previously reported by Den Heyer et al. (1988). Facilitatory effects of increasing the number of high-frequency neighbors of nonword stimuli were also observed in Experiment 2B. As noted by Den Heyer et al., these facilitatory neighborhood frequency effects are not readily interpretable within simple deadline model of the lexical decision task (since high-frequency words should generally provoke longer deadlines). However, the simulation studies with the multiple read-out model show that having the T and ∑ decision criteria vary as a function of
s values in early stages of processing allows the model to accurately predict the variations in mean RTs and percent errors in these experiments. This is because the summed lexical activity generated by nonword stimuli actually tends to diminish as the frequency of word neighbors increases. The model therefore provides a unified explanation for an otherwise apparently contradictory set of results.Experiment 3 investigated the effects of word frequency and neighborhood frequency in a perceptual identification and a lexical decision experiment. The presence of a single high-frequency neighbor within the target word's orthographic neighborhood provoked interference in the recognition of low-frequency target words in both tasks. This effect was greatly reduced for high-frequency targets in the perceptual identification task, and became facilitatory in the lexical decision task. The mechanism of lexical inhibition embodied in the model correctly predicts that high-frequency targets are less prone to interference from a high-frequency neighbor in the perceptual identification task. Due to their higher resting level activations, high-frequency stimuli can generate more inhibition on competing units and therefore reduce the inhibitory capacity of their competitors. Furthermore, the multiple read-out model captures the facilitatory effect observed in the lexical decision task by read-out from the ∑ decision criterion (it is this category of words that produced the highest
s values in the model).Thus, overall the model provides very accurate predictions concerning six different dependent variables measured in the lexical decision task, and provides a coherent explanation of variations in performance across different word recognition tasks. Furthermore, the stochastics implemented in the model in the form of variable decision criteria provide an excellent fit with the correct and incorrect, positive and negative RT distributions. With respect to the concept of functional overlap discussed in the introduction (see also Jacobs, 1994; Jacobs & Grainger, 1994), we have shown how variation in the use made of task-specific components allows the multiple read-out model to capture critical differences in the effects observed in the lexical decision, progressive demasking, and perceptual identification tasks.
PART II: FURTHER SIMULATION STUDIES ON ORTHOGRAPHIC NEIGHBORHOOD EFFECTS AND WORD FREQUENCY EFFECTS IN VISUAL WORD RECOGNITION
In Part II of this article, two failures of our previous simulation work (Jacobs & Grainger, 1992) are re-examined in the light of the multiple read-out model. These concern the interactive effects of word frequency and neighborhood density reported by Andrews (1989; 1992), and the interactive effects of word frequency and neighborhood frequency which were obtained in progressive demasking RTs and lexical decision error rate but not in lexical decision RTs (Grainger & Segui, 1990). Also, some recent conflicting results concerning the effects of neighborhood frequency in the lexical decision task (Sears et al., 1995) will be examined in the light of the model. The model will also be evaluated with respect to the critical issue of nonword lexicality and frequency blocking effects in lexical decision, recently raised by Stone and Van Orden (1993). Finally, the issue of word frequency effects in data-limited and response-limited paradigms recently raised by Paap and Johansen (1994) will be investigated.
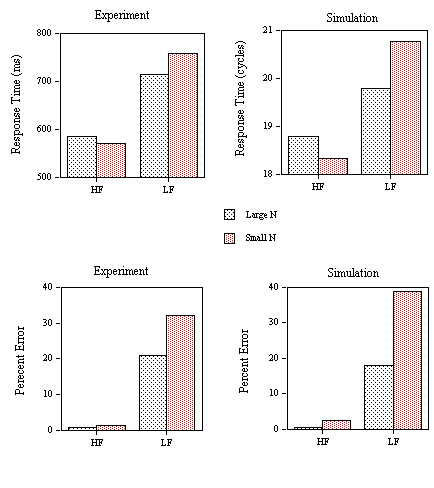
Figure 17. Obtained effects (Experiment) and predicted effects (Simulation) of neighborhood size (large N or small N) and word frequency (HF or LF) on response times and false negative errors to the word stimuli in the lexical decision experiment of Andrews (1992).
SIMULATION STUDY 1: Word Frequency X Neighborhood Density Interactions
In the first series of simulations using SIAM (Jacobs & Grainger, 1992), we reported that the model did not correctly simulate the facilitatory effects of neighborhood density observed with low-frequency words (Andrews, 1989; 1992). SIAM only implemented the M decision criterion for positive responses of the present model. Here we test the hypothesis that adding a ∑ threshold to the model will allow it to accommodate these facilitatory effects of neighborhood density. Moreover, it is hypothesized that the T threshold of the new model should also allow it to capture the effects in the error data reported by Andrews.
In Figure 17, we present the lexical decision results from Andrews (1992) along with the results of a new simulation with the multiple read-out model. The results show that the model captures the interaction between word frequency and neighborhood density observed by Andrews (1992) in the RT and error data. The model simulates the facilitatory effect of neighborhood density in RTs because words with many neighbors have higher
s values in the model and therefore are more likely to trigger a positive response with the ∑ threshold. This effect interacts with word frequency since high-frequency words reach the M criterion more rapidly than low-frequency words, and therefore leave less opportunity for the ∑ threshold to intervene. Moreover, since the T threshold is also adjusted as a function of s values, this allows the model to capture the same effects in the error data.As was noted in the discussion of Experiment 1, the model also predicts that these facilitatory effects of neighborhood density will depend on the characteristics of the nonword stimuli used as distracters in the experiment. In Experiment 1, we demonstrated that the effects of neighborhood density (when neighborhood frequency is controlled) are stronger when nonwords with low
s values (i.e., less word-like nonwords) are used as foils. This interaction between nonword lexicality and neighborhood density is accommodated by the model in terms of modifications of the ∑ and T thresholds during an experiment as a function of the s values of the nonword stimuli.Interestingly, in earlier experiments, Andrews (1989) reported that the effects of neighborhood density were only significant across items when the nonword stimuli were relatively unlike words (see Johnson & Pugh, 1994, for a similar result). Reducing the word-likeness of nonword stimuli is likely to reduce the
s values produced by these stimuli and therefore will result in a greater separation of the word and nonword s distributions. Consequently, participants could lower the criterion value of s used to trigger a positive response, while maintaining an acceptable false alarm rate (cf. discussion of Experiment 1). In Figures 18 and 19, we present two simulations run on Andrews' (1989) word stimuli with two ∑ threshold values (0.76 and 0.70). Note that the first value is identical to that used in the simulation of Andrews (1992) presented above. All other aspects of the simulation are identical to the previous simulation except that the T threshold setting criteria were adjusted to produce an average miss rate comparable to that obtained in the 1989 experiments.The results of the simulation show that the model does well in capturing the differences in neighborhood effects on RT and percent error with variations in the word-likeness of the nonword foils. This is particularly noticeable in the error data where facilitatory effects of neighborhood density to low-frequency words only appear in the presence of nonwords that are
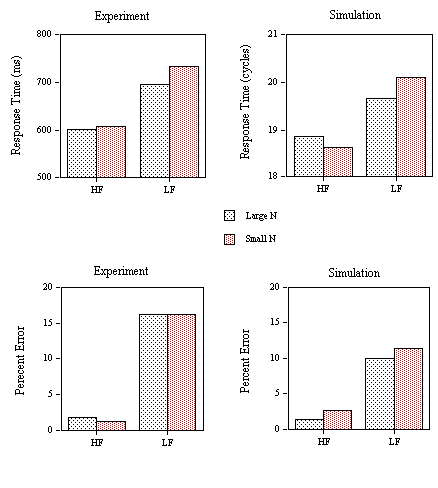
Figure 18. Obtained effects (Experiment) and predicted effects (Simulation) of neighborhood size (large N or small N) and word frequency (HF or LF) on response times and false negative errors to the word stimuli in the lexical decision experiment of Andrews (1989, Experiment 1).
relatively unlike words. The results of Andrews (1989) also show that effects of word frequency are slightly smaller with less word-like nonwords, an aspect of her results that is also captured by the present simulation. We shall return to an examination of word frequency and nonword lexicality interactions in Simulation Study 4.
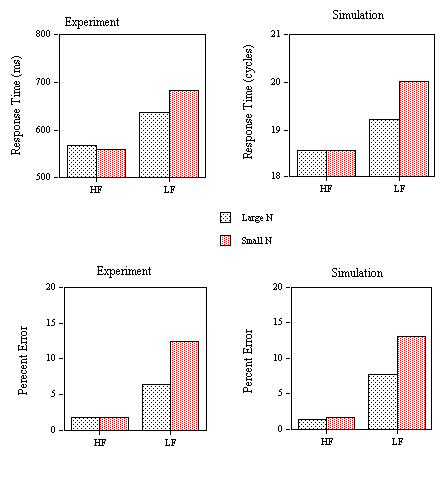
Figure 19. Obtained effects (Experiment) and predicted effects (Simulation) of neighborhood size (large N or small N) and word frequency (HF or LF) on response times and false negative errors to the word stimuli in the lexical decision experiment of Andrews (1989, Experiment 2) with less word-like nonwords.
Snodgrass and Mintzer (1993), using the same word stimuli as Andrews (1989) in a perceptual identification experiment (percent correct identifications at fixed stimulus exposures), obtained inhibitory effects of neighborhood density. These authors argued that the perceptual identification task and related paradigms (such as progressive demasking and identification threshold measures) are a more direct reflection of the visual word recognition process. On the basis of this argument, removing the ∑ and T criteria from the multiple read-out model (as in the simulations of the progressive demasking paradigm of Experiment 1A and the perceptual identification task of Experiment 3A), should produce inhibitory effects of neighborhood density. As indicated in our previous simulations using Andrews' (1989) stimuli (Jacobs & Grainger, 1992), this is exactly what happens. We obtain a 0.97 cycle inhibitory effect of neighborhood density when the ∑ and T thresholds are removed from the model.
SIMULATION STUDY 2: Word Frequency X Neighborhood Frequency Interactions
The simulations presented in our earlier study (Jacobs & Grainger, 1992) were all error free in the sense that the model always correctly recognized the stimulus. In lexical decision experiments where error rate does not significantly vary across conditions, these error-free simulations provided a good fit with observed RTs in experiments investigating neighborhood frequency (Grainger & Segui, 1990), masked orthographic priming (Segui & Grainger, 1990), and masked repetition priming (Forster & Davis, 1984; Segui & Grainger, 1990). However, there is one simulation study presented by Jacobs and Grainger (1992) that deserves closer examination. This concerns the effects of stimulus frequency and neighborhood frequency in the lexical decision and the progressive demasking tasks studied by Grainger and Segui (1990).
Grainger and Segui (1990) observed that the effects of neighborhood frequency interacted with the effects of word frequency in progressive demasking latencies, but were additive in lexical decision latencies. The percent errors in the lexical decision task did, however, show the same pattern of effects as the progressive demasking RTs. Larger effects of neighborhood frequency were observed with low-frequency words. In the multiple read-out model, simulations without the ∑ and T criteria (as was the case with SIAM) should correspond more closely to data obtained with the progressive demasking task. Accordingly, the results of a simulation run on SIAM (Jacobs & Grainger, 1992) showed the same absence of an interaction between word frequency and neighborhood frequency as found in the progressive demasking data. Here we test the prediction that adding the ∑ and T thresholds will allow the model to simulate the lexical decision results.
The original results of Grainger and Segui (1990) and two new simulation studies (with the M criterion only, and with the ∑ and T criteria added), are shown in Figure 20. The results of the first simulation (upper panel) are a direct replication of the study presented by Jacobs and Grainger (1992). They demonstrate that a response criterion set on word unit activity (M) predicts the interaction between word frequency and neighborhood frequency effects obtained in the progressive demasking task (cf. Experiment 3A of the present article). Moreover, adding a temporal deadline (T) and a criterion set on overall lexical activity (∑) allows the model to
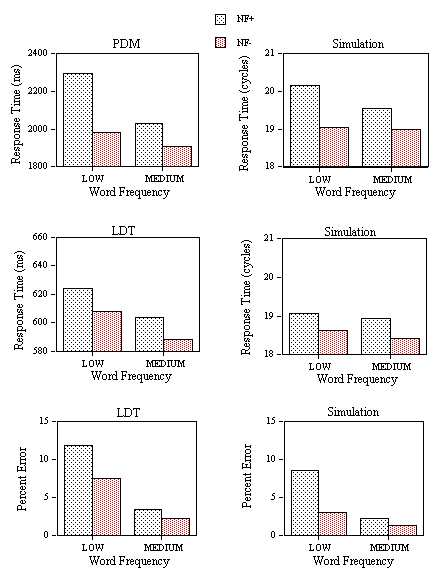
Figure 20. Obtained effects (Experiment) and predicted effects (Simulation) of neighborhood frequency (NF+ at least one higher frequency neighbor; NF- no higher frequency neighbors) and word frequency (low or medium) on response times in the progressive demasking experiment (PDM) and both response times and false negative errors in the lexical decision experiment (LDT) of Grainger and Segui (1990).
capture the additive effects of word and neighborhood frequency obtained in the lexical decision RTs (middle panel), as well as the interactive effects obtained in the percent errors (bottom panel). Adding a temporal deadline to the model provides an elegant means of explaining why the interaction appeared in the error rates but not in RTs in the lexical decision task. Adding an upper time limit will simply transform extreme RTs (lying above this limit) into errors. Therefore, words that take very long to recognize (the low-frequency stimuli with high-frequency neighbors) will generate an increase in error rate rather than an increase in average RT. Adding the ∑ threshold also contributes to removing the interaction between neighborhood frequency and word frequency in the RT data. The
s values of the stimuli used by Grainger and Segui (1990) vary across categories in a way that reduces the effects of neighborhood frequency for the low-frequency words without modifying this effect in the medium-frequency words. Thus, Simulation Study 2 provides a further demonstration (see Experiment 1) that the multiple read-out model captures the relation between the information processing required in normal word recognition on the one hand, and in the laboratory tasks of lexical decision and progressive demasking on the other.
SIMULATION STUDY 3: Reconciling Conflicting Results Concerning Neighborhood Frequency Effects
In a recent study, Sears et al. (1995) systematically failed to observe neighborhood frequency effects in the lexical decision task while obtaining clear facilitatory effects of neighborhood density. Since the multiple read-out model has, up to now, repeatedly predicted inhibitory effects of neighborhood frequency in lexical decision performance, the results of Sears et al. appear, at first sight, damaging for our approach. However, as noted in Experiment 1 of the present paper, neighborhood frequency also correlates with summed lexical activity (albeit to a lesser degree than neighborhood density). Whether or not one observes inhibitory effects of neighborhood frequency will therefore depend on the tradeoff between increased lexical inhibition (words with high-frequency neighbors generate more lexical inhibition) on the one hand, and increased use of the ∑ criterion (words with high-frequency neighbors tend to have higher
s values) on the other hand. Thus, within the framework of the multiple read-out model, the failure to obtain inhibitory effects of neighborhood frequency could be due to the participants in Sears et al.'s experiments having made excessive use of the ∑ criterion as opposed to the M criterion for positive responses. In the following simulations, we will demonstrate that adjusting the amount of use made of the ∑ criterion can indeed allow the multiple read-out model to capture the main results obtained by Sears et al. (1995) with respect to effects of neighborhood frequency.For the present purposes the critical manipulations of Sears et al. occur in Experiments 1, 4a, and 5 of their article. In Experiment 1 neighborhood density was crossed with word frequency and neighborhood frequency in a 2X2X2 design. In Experiment 4 (if one excludes the hermit word condition) then neighborhood density (large N vs. small N) was crossed with neighborhood frequency (0, 1, and more than one high-frequency neighbor) in a 2X3 design. Also, the effect of number of neighbors (0, small, and large) was tested in the nonword stimuli of Experiment 4a. Finally, in Experiment 5 neighborhood density was crossed with neighborhood frequency in low-frequency word stimuli in the presence of nonwords with large N values. The critical results of these experiments along with the simulation results of the multiple read-out model are provided in Figures 21-24.
In the simulation studies, the ∑ and T criteria of the multiple read-out model were adjusted in order to simulate the major effects reported in Experiments 1, 4a, and 5 of Sears et al.'s paper
2 . These simulations are constrained by keeping average false positive and negative error rate in line with those reported by Sears et al. Since error rate is strongly affected by modifications of the ∑ and T criteria, the task is to find a particular setting of these criteria, via fine tuning (minor adjustments of these parameters around the values used in the previous simulations), that will generate the pattern of results observed in the experimental data.Apart from the main effects of word frequency and neighborhood density (which the model evidently captures, see Simulation Study 1) the results of Experiment 1 can be summarized in terms of an absence of interaction between neighborhood density and word frequency, and the presence of an interaction between neighborhood density and neighborhood frequency. The facilitatory effects of neighborhood density only appeared in the words with high-frequency neighbors. The multiple read-out model captures this pattern of effects in the RTs and percent errors (Figures 21 and 22).
Apart from the replication of a facilitatory effect of neighborhood density (which once again the model evidently captures), the major results of Experiment 4a can be summarized in terms of a small facilitatory effect of increasing numbers of high-frequency neighbors on RTs and accuracy to word stimuli, and a strong inhibitory effect of neighborhood density on RTs and accuracy to nonword stimuli. As can be seen in Figure 23, although the pattern of results for the word stimuli predicted by the model fails to capture the minor details, the multiple read-out model does capture the major trends in the data. That is, the model successfully captures the absence of an inhibitory effect of neighborhood frequency in the word data and the presence of a strong inhibitory effect in the nonword data.
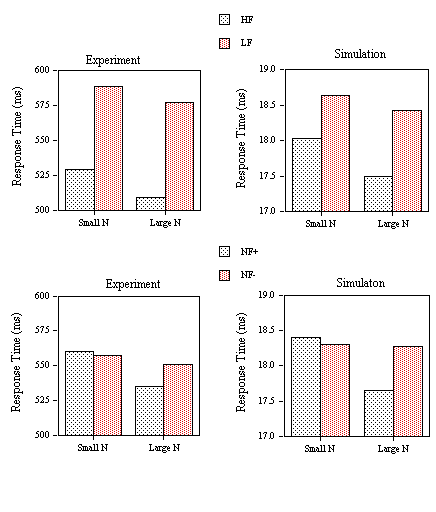
Figure 21. Obtained effects (Experiment) and predicted effects (Simulation) of neighborhood size (large N or small N) and word frequency (HF or LF) in the upper panel, and neighborhood size and neighborhood frequency (presence (NF+) or absence (NF-) of higher frequency neighbors) in the lower panel, on response times to the word stimuli in the lexical decision task of Sears et al. (1995, Experiment 1).
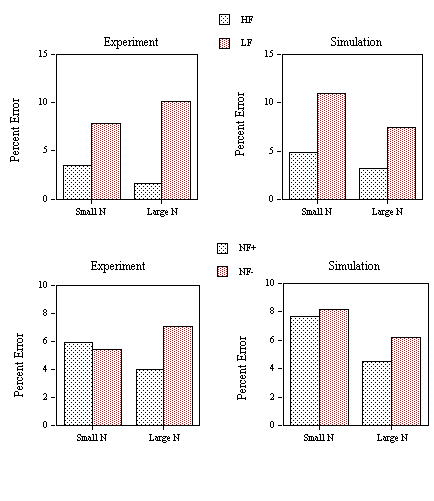
Figure 22. Obtained effects (Experiment) and predicted effects (Simulation) of neighborhood size (large N or small N) and word frequency (HF or LF) in the upper panel, and neighborhood size and neighborhood frequency (presence (NF+) or absence (NF-) of higher frequency neighbors) in the lower panel, on percentage of errors to the word stimuli in the lexical decision task of Sears et al. (1995, Experiment 1).
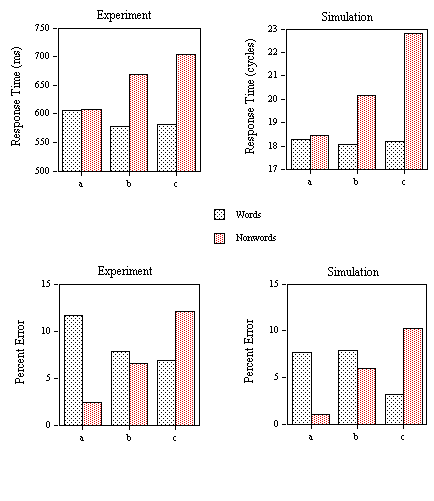
Figure 23. Obtained effects (Experiment) and predicted effects (Simulation) of number of higher frequency neighbors of word stimuli (a=0, b=1, c >1) and number of word neighbors of nonword stimuli (a=0, b=small N, c=large N) on response times and percentage of errors in the lexical decision task of Sears et al. (1995, Experiment 4a).
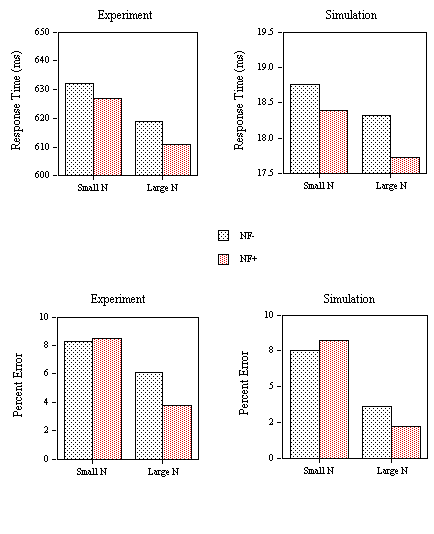
Figure 24. Obtained effects (Experiment) and predicted effects (Simulation) of neighborhood size (large N or small N) and neighborhood frequency (presence (NF+) or absence (NF-) of higher frequency neighbors) on response times and percentage of errors to the word stimuli in the lexical decision task of Sears et al. (1995, Experiment 5).
Sears et al.'s Experiment 5 was designed as a further test of neighborhood frequency effects in the presence of nonword stimuli with large N values. Nonwords with large numbers of orthographic neighbors should also have large
s values. Thus, one might expect that use of the ∑ criterion should be impossible in such conditions. As a result, significant inhibitory effects of neighborhood frequency should appear. However, Sears et al. observed a small but significant facilitatory effect of neighborhood density in both the RT and the error data, and neighborhood frequency had a non-significant facilitatory effect on both of these variables. An examination of the distribution of the s values of Sears et al.'s word and nonword stimuli showed that one can find critical values on this dimension that allow the multiple read-out model to simulate the observed pattern of effects. As can be seen in Figure 24, the model does an excellent job in capturing this pattern of results, even to the point of simulating the trend toward an interaction between neighborhood size and neighborhood frequency in the error data.The successful application of the multiple read-out model to the critical aspects of Sears et al.'s (1995) lexical decision results is another example of how the concept of variable response criteria can help resolve apparently conflicting results in this field. In particular, it appears that the total lexical activity (
s) generated by a given stimulus can drive two response criteria that are specifically involved in generating positive and negative responses in a lexical decision experiment. The fact that multiple response criteria can be used to generate the same response (i.e., the ∑ and M criteria for a positive response) complicates the interpretation of experimental data. The conflicting results of Sears et al. and those reported by Grainger and his colleagues concerning effects of neighborhood frequency is a case in point. Words with high-frequency orthographic neighbors tend to generate more lexical inhibition. This increases the time taken to reach the M criterion, thus generating longer RTs and more false negative errors in the lexical decision task. However, these same words will also tend to have higher s values than words with no high-frequency neighbors, resulting in less time taken to reach the ∑ criterion and therefore faster RTs and less false negative errors. This implies that the effects of neighborhood frequency can vary from being inhibitory, null, to facilitatory depending on the relative use made of these two positive criteria (i.e., how low the ∑ criterion is set).In Simulation Study 2 of the present paper, the multiple read-out model successfully captured the different pattern of effects obtained in the progressive demasking and lexical decision tasks by Grainger and Segui (1990), by adding or removing the ∑ criterion of the model. As pointed out by Grainger and Segui, the inhibitory effects of neighborhood frequency are much larger in the progressive demasking task compared to the lexical decision task (expressed as a percentage of average RT: 10.6% compared to 2.6%). From the above analysis, it should be clear that the multiple read-out model correctly predicts that inhibitory effects of neighborhood frequency will be much larger in perceptual identification tasks that prohibit the use of the ∑ criterion. This analysis leads us to make one clear prediction to be tested in further experimentation. The stimuli in Sears et al.'s experiments that showed no effect of neighborhood frequency in the lexical decision task should show inhibitory effects in a perceptual identification task. With respect to effects of neighborhood density, the results of Snodgrass and Mintzer (1993) are encouraging on this point. Such inhibitory effects of orthographic neighborhoods in perceptual identification tasks have been replicated in three recent studies in Spanish, Dutch, and French (Carreiras, Perea, & Grainger, submitted; Van Heuven, Dijkstra, & Grainger, submitted; Ziegler et al., submitted).
In the present research, increasing the number of high-frequency neighbors resulted in inhibitory effects in the progressive demasking task (Experiment 1A), but no effect in the lexical decision task (Experiment 1B). Furthermore, the size of neighborhood frequency effects diminished in the presence of nonwords with low
s values in Experiment 1C, and when speed was encouraged over accuracy in Experiment 1D. Finally, in Experiment 3 the presence of a single high-frequency neighbor did not affect overall performance in a lexical decision task but produced strong inhibition in a perceptual identification task. We therefore have several reasons to believe that the same stimuli that produced a null effect of neighborhood frequency in Sears et al.'s (1995) experiments would produce an inhibitory effect in a perceptual identification task. Nevertheless, there may be additional reasons for the discrepancy between Sears et al.'s and our own results, such as the different languages used in these experiments (English and French, that differ notably in terms of rime consistency), and the letter position that distinguishes the word target from its orthographic neighbor (a factor that has generally not been systematically controlled). The present analysis shows that these two sets of apparently conflicting results are not necessarily incompatible within the framework of the multiple read-out model.SIMULATION STUDY 4: Nonword Lexicality And Frequency Blocking Effects
In Part 1, we presented some empirical results showing that nonword lexicality interacted with effects of neighborhood frequency and density in the lexical decision task. In Simulation Study 1, the interaction with neighborhood density was also discussed with respect to the results of Andrews (1989). The multiple read-out model captures these subtle interaction effects via modifications in the ∑ decision criterion as a function of the degree of overlap of the
s values of word and nonword stimuli used in an experiment.In the present study we examine another important effect in the lexical decision literature referred to as the frequency blocking effect. This corresponds to the observation that word frequency effects in the lexical decision task are modified by the frequencies of other words in the list (Dorfman & Glanzer, 1988; Glanzer & Ehrenreich, 1979; Gordon, 1983; Stone & Van Orden, 1993). Thus, both the frequency blocking and nonword lexicality manipulations involve modifications of list composition (i.e., modification of the characteristics of non-target stimuli in a given experimental list). The frequency blocking phenomenon has often been reported as the single most constraining result with respect to models of the lexical decision task, since no single model can purport to handle all aspects of this phenomenon (see Dorfman & Glanzer, 1988; Stone & Van Orden, 1993, for detailed discussions on this point).
The main results concerning the frequency blocking phenomenon are summarized below:
1) RTs to high-frequency words are faster when all the accompanying words are also high-frequency (blocked condition) compared to when both high and low-frequency words (mixed condition) appear in the experiment (Glanzer & Ehrenreich, 1979; Gordon, 1983; Stone & Van Orden, 1993). The difference in RT between the blocked and mixed presentation conditions is referred to as the frequency blocking advantage.
2) The frequency blocking advantage is largest for high-frequency words, reduced for medium-frequency words, and absent for low-frequency words (Gordon, 1983), at least when no pseudohomophones are included among the nonword foils (Stone & Van Orden, 1993), and when speed rather than accuracy is stressed (Dorfman & Glanzer, 1988).
3) The frequency blocking advantage in RTs is not the result of SATOs because an increase in accuracy can accompany the RT advantage (Dorfman & Glanzer, 1988). Nevertheless, faster RTs to blocked high-frequency words are generally accompanied by a slight increase in error rate (Dorfman & Glanzer, 1988; Glanzer & Ehrenreich, 1979; Gordon, 1983; Stone & Van Orden, 1993).
4) RTs to nonwords are faster (for relatively stable levels of accuracy) when the list contains a high proportion of high-frequency words (Dorfman & Glanzer, 1988; Glanzer & Ehrenreich, 1979; Stone & Van Orden, 1993).
Many recent accounts of the frequency blocking phenomenon use criterion adjustments to explain the basic effect. In the blocked high-frequency condition it is hypothesized that the distributions of the word and nonword stimuli overlap less than in the mixed frequency condition. Overlap is defined in terms of some dimension such as familiarity / meaningfulness (Balota & Chumbley, 1984), orthographic error scores (Seidenberg & McClelland, 1989), or word activation or accumulation rate (Gordon, 1983; Stone & Van Orden, 1993). Accordingly, in the blocked high-frequency condition, participants can lower the criterion used for positive responses in the lexical decision task. Consequently word units will reach threshold with less accumulated evidence, or a greater percentage of fast positive responses will be generated on the basis of some evaluation of word-likeness. However, only Balota and Chumbley's (1984) and Stone and Van Orden's (1993) models make specific predictions with respect to frequency blocking effects on negative RTs and error rates. Only these models that can therefore be fully evaluated on the basis of the above effects.
Balota and Chumbley (1984) proposed a variant of SDT models using a rechecking mechanism (Atkinson & Juola, 1973; Krueger, 1978). Their model qualitatively accounts for frequency effects on mean RTs in terms of a familiarity/meaningfulness judgment that is independent of lexical processing (i. e. based on extra-lexical information). Balota and Chumbley argued that a "fast-positive" criterion on the familiarity / meaningfulness dimension is lowered in the blocked high-frequency condition. In addition, a second "fast-negative" criterion can be raised, thus increasing the percentage of nonwords lying above this criterion, and therefore lowering correct reject RTs. Stimuli generating values between these two criteria are given further analysis before response. Consequently, RT trades off with error rate as these two criteria are adjusted. This model therefore incorrectly predicts that the decrease in correct positive and negative RTs in the blocked high-frequency condition must necessarily be accompanied by an increase in both false positive and false negative responses (Dorfman & Glanzer, 1988).
Stone and Van Orden (1993) presented a canonical random walk model of the lexical decision task based on Gordon's (1983) model. Their model is elaborated to a point that allows precise (albeit qualitative) predictions concerning responses to nonwords. These predictions focus on the effects of nonword foil lexicality, word frequency, and frequency blocking. The model does well in accommodating the interactive effects of word frequency and nonword lexicality, but has difficulty in capturing the full pattern of results obtained with the frequency blocking manipulation.
Stone and Van Orden's explanation of the frequency blocking effect is expressed in terms of a trade-off between i) modifications in the hit criterion and ii) modifications in the accumulation rates for word and nonword responses as a function of frequency blocking. In the blocked high-frequency condition, the hit criterion is lowered relative to the mixed frequency condition thus giving rise to faster hit RTs. However, the word accumulation rate is lowered (and the nonword accumulation rate raised) in the pure high-frequency condition thus slowing hit RTs. Stone and Van Orden argue that for high-frequency words, the RT gain from a lower hit criterion is greater than the cost caused by a slower accumulation rate, whereas for low-frequency words, the cost and gains balance out.
The following predictions concerning nonword RTs, and both false positive and negative error rates, follow from Stone and Van Orden's explanation of the interaction between word frequency and effects of frequency blocking (Stone & Van Orden did not examine these predictions themselves). The model predicts that there should be a frequency blocking advantage for nonword RTs in the high-frequency condition, and a disadvantage in the low-frequency condition. This follows from the different nonword accumulation rates (inversely related to the accumulation rate for words) in these two conditions. Stone and Van Orden observe exactly this pattern of effects in their experiments (but see Glanzer & Ehrenreich, 1979, for different results concerning nonword RTs in the blocked low-frequency condition).
The model predicts a frequency blocking advantage in the error rates to high-frequency words and a disadvantage for the low-frequency words. This follows from the different word accumulation rates in these two conditions, and the fact that the negative response criterion does not change. However, contrary to these predictions Stone and Van Orden (1993) observe a slight disadvantage for the high-frequency words (also observed by Dorfman & Glanzer, 1988; Glanzer & Ehrenreich, 1979; and Gordon, 1983), and no effect for the low-frequency words. Furthermore, the model predicts an increase in errors to nonword stimuli in the blocked high-frequency condition (due to a lower hit criterion and a faster accumulation rate for nonwords), and a decrease in these errors in the blocked low-frequency condition (due to a higher hit criterion and a slower accumulation rate for nonwords). However, Stone and Van Orden observe a very small (0.5%) increase in false positive errors in the blocked high-frequency condition, and a large increase in these errors (6.1%) in the blocked low-frequency condition. Moreover, Glanzer and Ehrenreich (1979) observed a slight decrease in false positive errors (0.3%) in the blocked high condition, and an increase in errors (1.5%) in the blocked low condition.
Clearly, the canonical random walk model fails to capture these aspects of the frequency blocking phenomenon. A similar failure was noted by Stone and Van Orden (1993) themselves with respect to their model's account of nonword lexicality effects. Their model predicted that false negative errors (misses) should decrease as nonword foil lexicality increases. This is because the negative response criterion is raised as nonword lexicality increases, while the word accumulation rate remains unchanged. However, Stone and Van Orden observed a significant increase in false negative responses to low-frequency words with higher levels of nonword lexicality. We shall return to this particular point in a discussion of the simulation results presented below.
The multiple read-out model provides a unified account of frequency blocking and nonword lexicality effects in the lexical decision task. The model captures the effects of the frequency blocking phenomenon much in the same way as it captures the effects of nonword lexicality effects (see Experiment 1 and Simulation Study 1). This basically involves strategic adjustments of the ∑ and T criteria as a function of the frequency distribution of word stimuli, much in the same way as these parameters are thought to be adjusted as a function of nonword characteristics. The fact that two different criteria (∑ and T) are strategically adjustable in the multiple read-out model allows it to capture all aspects of the frequency blocking phenomenon discussed above. As the proportion of high-frequency words increases, so does the proportion of words that generate critical levels of
s in early stages of processing (simply because high-frequency words tend to generate higher s values than low-frequency words). Thus, faster responses can be generated in the model via two criterion adjustments: 1) In order to reduce positive RTs, the ∑ criterion for a positive response is lowered. 2) In order to reduce negative RTs, we raise the critical s value required to shift the T decision criterion higher. This increases the number of nonwords that generate a low temporal deadline. By combining these two adjustments, the gain in positive RT does not necessarily provoke an increase in false positive errors, since the nonwords will have less time, on average, to reach the ∑ criterion. Moreover, the adjustments of the T criterion will cause an increase in false negative errors, which is typically observed in experimentation.
Figure 25. Obtained effects (Experiment) and predicted effects (Simulation) of nonword foil lexicality (legal or illegal) on response times and error rates to high-frequency (HF) and low-frequency (LF) word stimuli and nonword stimuli (NW) in the lexical decision experiment of Stone and Van Orden (1993, Experiment 1).
Figure 26. Obtained effects (Experiment) and predicted effects (Simulation) of frequency blocking (blocked or mixed frequency lists) on response times and error rates to high-frequency (HF) and low-frequency (LF) word stimuli in the lexical decision experiments of Stone and Van Orden (1993, Experiments 1 and 3).
SIMULATION
As a complete test of the model's unified account of frequency blocking and nonword lexicality effects we used Stone and Van Orden's (1993) stimuli in a new simulation study. To simulate the effects of frequency blocking, the critical
s values, used to modify the T criterion after 7 cycles of processing, were lowered in the blocked low-frequency condition and raised in the blocked high-frequency condition relative to the mixed frequency condition. Also, the mean value of the ∑ decision criterion was lowered in the pure high-frequency condition relative to both the blocked low-frequency and mixed frequency conditions. When simulating the effects of nonword lexicality, only the mean value of the ∑ decision criterion was modified. Lower values were adopted with decreasing levels of nonword lexicality. The mean values of the T criterion were not adjusted in this simulation.In Figures 25-27, Stone and Van Orden's (1993) experimental data are presented along with simulation results from the multiple read-out model. The conditions represented in these figures concern the legal vs. illegal foil conditions with mixed frequencies tested in their Experiment 3, and the legal foil, blocked frequency conditions of their Experiment 1. Figure 25 provides the results concerning the nonword lexicality manipulation. As can be seen from this figure, the multiple read-out model accurately reflects the interaction between effects of nonword lexicality and stimulus category (high-frequency word, low-frequency word, or nonword) in the RT data. Moreover, the model captures the increase in error rate to low-frequency words and nonwords that accompanies an increase in nonword lexicality, while capturing the fact that error rates to high-frequency words vary little.
Concerning frequency blocking effects on word stimuli, it can be seen in Figure 26 that the model correctly simulates the interaction between this factor and word frequency in both the RT and error data. As can be seen in Figure 27, the model also captures the effects of frequency blocking on nonword stimuli, both in the RT and error data. It is important that the model simulates variations in false positive and negative errors in the frequency blocking manipulation, because this is one aspect of the results that proved particularly problematical for Stone and Van Orden's (1993) model (the only alternative model to provide such detailed predictions).
Figure 27. Obtained (Experiment) and predicted (Simulation) response times and error rates to nonword stimuli in the blocked high-frequency (HF), blocked low-frequency (LF) and mixed frequency conditions tested by Stone and Van Orden (1993, Experiments 1 and 3).
SIMULATION STUDY 5: The Case Of The Vanishing Frequency Effect
One of the central claims of Paap et al. (1982) with respect to the activation verification (AV) model of visual word recognition, is that word frequency effects should not occur when the stimulus is briefly presented and followed by a pattern mask. In the AV model, a written word is recognized after two successive stages of processing, referred to as encoding and verification. Stimulus word frequency exerts its influence during the verification phase, but not during early stimulus encoding. Since it is hypothesized that brief presentation and backward masking prevent verification, the model predicts that word frequency effects should not be observed in these conditions. There are, however, results reported in the literature that suggest that word frequency effects can be observed in such conditions (e.g., Allen, McNeal, & Kvak, 1992; Dobbs, Friedman, & Lloyd, 1985, but see Paap & Johansen, 1994, for a critique of these studies). The present simulation study takes a look at the other side of the coin: Why are word frequency effects so elusive in data-limited presentation conditions? Simulation Study 5 examines whether the multiple read-out model can successfully capture the fact that word frequency effects obtained with a given stimulus set in a speeded lexical decision task disappear when tested in a forced-choice, data-limited situation (Paap & Johansen, 1994).
Since IA models of visual word recognition, including the multiple read-out model, code word frequency in terms of the resting level activation of word detector units, one might expect them to predict the presence of word frequency effects in data-limited, forced-choice paradigms such as the Reicher-Wheeler task. This category of model must therefore explain why word frequency effects are generally not robust in the Reicher-Wheeler task (Günther, Gfroerer, & Weiss, 1984). In a recent article (Grainger & Jacobs, 1994), we argued that it might not be the use of data-limited procedures as such that renders the word frequency effect so hard to find (as predicted by the AV model), but rather the use of forced-choice methodology in the Reicher-Wheeler task. The very fact that many perceptual identification experiments (including the present Experiment 3) find robust word frequency effects, is good evidence that it is not data-limited presentation per se that makes word frequency effects so elusive. We argued that two factors contribute to the elusive nature of word frequency effects in the Reicher-Wheeler task: 1) Forced-choice methodology reduces effect sizes by exactly one half compared to a free report situation; and 2) read-out from single letter representations reduces the influence of lexical factors in the Reicher-Wheeler task.
Paap and Johansen's (1994) recent failure to obtain word frequency effects in data-limited conditions in both the Reicher-Wheeler and the lexical decision task, using stimuli that produced a robust word frequency effect in standard response-limited lexical decision, has further complicated the picture. In their Experiment 2, participants were given standard Reicher-Wheeler instructions (forced choice between two alternative letters) and were then asked to do the same with respect to a word/nonword decision. The forced-choice lexical decision data were almost identical to the forced-choice data for letters in words, thus suggesting that letter-in-word report accuracy can be entirely accounted for by percent correct word identification in this experiment. The results of their Experiment 2 show non-significant, non-monotonic effects of word frequency (see Figure 28, bottom panel). High-frequency words produced slightly better levels of accuracy than both low-frequency words and very high-frequency words. Since the lexical decision results were almost identical to the results of letter-in-word report accuracy, one can no longer argue that the word frequency effect is reduced by read-out from the letter rather than the word level. This result therefore stands as a challenge to the multiple read-out model.
SIMULATION
The speeded lexical decision results were simulated using the M, ∑, and T criteria of the multiple read-out model as in previous simulations of lexical decision data. The results of this simulation using the very high frequency, high frequency, and low-frequency word stimuli tested by Paap and Johansen are given in Figure 28. To simulate performance in the data-limited, forced-choice experiment, we adopted exactly the same simulation procedure as previously used for the perceptual identification task of Experiment 3. Percent correct word identification (PC) was transformed into two-alternative forced-choice percent correct (FC) with the following formula: FC=PC+((100-PC)/2). This assumes that in performing a forced-choice task with word stimuli, the participants either recognize the word and therefore respond correctly, or they do not recognize the word and therefore respond at random. It is of course possible that on word trials, participants sometimes erroneously perceive another word. This, however, would have no effect on lexical decision forced-choice accuracy. Furthermore, because some of the erroneously perceived words also contain the target letter at the correct position, this will have little effect on forced-choice accuracy to letters.
The simulation results presented in Figure 28, show that the multiple read-out model correctly simulates strong word frequency effects in both the RT and percent errors in a speeded lexical decision task (Paap & Johansen, Experiment 1), and the absence of this effect in the data-limited, forced-choice situation (Paap & Johansen, Experiment 2). Most notably, the model correctly simulates small, non-monotonic effects of word frequency in the forced-choice paradigm, with high-frequency words producing slightly better levels of performance than both low-frequency words and very high-frequency words.
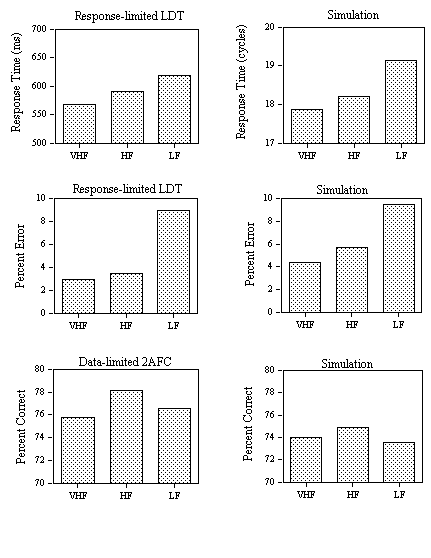
Figure 28. Obtained (Experiment) and predicted (Simulation) response times and error rates in a response-limited lexical decision task, and percent correct report in a data-limited 2AFC experiment to the very high-frequency (VHF), high-frequency (HF) and low-frequency (LF) words tested by Paap and Johansen (1994).
Clearly, the very high-frequency words are the critical category in these experiments, because they switch from giving the best performance in the response-limited paradigm (fastest RTs and lowest error rate) to worst performance in the data-limited, forced-choice paradigm (lowest percent correct). Indeed, when the very high-frequency word category is excluded from the statistical analysis, then Paap and Johansen do find a significant effect of word frequency in the Reicher-Wheeler task. What, therefore, is so particular about the very high-frequency words tested in these experiments that provokes a performance decrement in data-limited conditions? One possible answer is already provided in Paap and Johansen's Table 2. The very high-frequency words have bigram frequencies almost twice as great as the words from the other frequency categories. It is often assumed that bigram frequency positively correlates with performance in visual word recognition tasks (e.g., Massaro & Cohen, 1994). However, in previous and ongoing experimental work, we have systematically observed inhibitory effects of positional letter frequency (a variable that is highly correlated with bigram frequency). For example, in masked priming experiments with partial-word primes, we observed that RTs to target stimuli increased as the positional frequencies of letters shared by the prime and target increased (Grainger & Jacobs, 1993). In recent unpublished experiments, it was found that percent correct word report in a perceptual identification task was inversely related to the average positional letter frequency of target stimuli (with orthographic neighborhoods tightly controlled). Moreover, these inhibitory effects of positional letter frequency tended to become facilitatory in a lexical decision task. Together, this might explain why the very high-frequency words tested by Paap and Johansen produced the best performance in the response-limited lexical decision task.
It appears that positional letter frequency exerts an inhibitory influence on visual word recognition under data-limited presentation conditions (brief exposures and pattern masking), which disappears in response-limited conditions. This makes sense within the interactive-activation framework, since positional letter frequency determines the degree of activation of all words that have minimum orthographic overlap (one letter) with the target. As the target word's activation level rises, the inhibition on all other word units increases. Therefore, the activation levels of all words sharing only one letter with the target will quickly return to resting level. As processing continues, only full orthographic neighbors will eventually have any significant influence on target word activation. One-letter neighbors will therefore only influence the activation level of the target word during the earliest phases of processing. The same will be true for the two-letter neighbors indexed by measures of positional bigram frequency. This therefore explains why the model successfully captures the fact that the very high-frequency words (with high positional bigram frequencies) tested by Paap and Johansen suffered inhibition only in data-limited presentation conditions.
DISCUSSION OF PART II
In Part II of our tests of the multiple read-out model, several subtle interactions between the effects of word frequency, orthographic neighborhoods, list composition, nonword lexicality, and stimulus presentation conditions were examined. Although such interactions have proved to be major obstacles for models of visual word recognition in the past, the multiple read-out model successfully simulated all of these results. Next we provide a brief recapitulation of the main results and provide an analysis of the model's performance in each case.
Neighborhood frequency effects interact with word frequency in progressive demasking RTs, but this interaction only appears in false negative error rate in the lexical decision task (Grainger & Segui, 1990). Performance in the lexical decision task is captured in the multiple read-out model by adding the ∑ and T decision criteria, not used in simulating performance in the progressive demasking task. Words differing in neighborhood frequency reach the M decision criterion with different latencies due to variations in lexical inhibition. However, since these different categories of words also vary in terms of
s values in the model, adding a ∑ criterion provokes an interaction with the basic neighborhood frequency effect obtained with the M criterion. Also, adding a temporal deadline to the model causes some extreme RTs, resulting from excessive lexical inhibition, to be transformed into false negative errors. This allows the model to capture SATO phenomena in general, and the appearance of effects in error rate rather than RTs in the lexical decision task, in particular.The multiple read-out model accommodates the facilitatory effects of neighborhood density on positive lexical decision latencies to word stimuli (Andrews, 1989; 1992) because high density words generate higher
s values in the model and therefore reach the ∑ criterion before low density words. The model simulates the interaction between neighborhood density and word frequency by the greater involvement of the ∑ decision criterion in responses to low-frequency stimuli. High frequency words typically reach the M decision criterion before critical s values are reached. Moreover, since less word-like nonwords generate lower s values, including such stimuli in an experiment allows subjects to strategically reduce the ∑ decision criterion for positive responses. In this way, the model correctly predicts that larger effects of neighborhood density are obtained with less word-like nonwords (Experiment 1; Andrews, 1989). This aspect of the model also allows it to capture the interaction between nonword lexicality and stimulus word frequency (Stone & Van Orden, 1993).In a similar way, the multiple read-out model captures the null effect of neighborhood frequency in the lexical decision experiments of Sears et al. (1995). Words with high-frequency neighbors tend to have higher
s values than words without high-frequency neighbors. Thus, the inhibitory effects of neighborhood frequency (resulting from higher levels of lexical inhibition with these stimuli) can be more or less diluted by a facilitatory component arising from involvement of the ∑ criterion. The simulations using Sears et al.'s word and nonword stimuli show that the multiple read-out model can accommodate such null effects of neighborhood frequency in a principled, theoretically meaningful, manner.The frequency-blocking phenomenon, often used as critical constraining data for models of lexical decision, presented no obstacle for the multiple read-out model. The model captures these effects, much in the same way as it captures effects of nonword foil lexicality, by variations in the critical
s values that determine both the ∑ and T decision criteria. High frequency words tend to generate higher levels of s in the model than low-frequency words. Increasing the proportion of high-frequency words in an experiment therefore increases the proportion of words compared to nonwords that reach critical levels of s. In blocked high-frequency lists, the average ∑ and T decision criteria can be lowered, thus reducing correct positive and negative RTs. In the blocked low-frequency condition, on the other hand, the T criterion is raised in order to avoid an increase in false negative errors. This results in longer correct negative RTs.The multiple read-out model captured the absence of word frequency effects in a data-limited, forced-choice experiment, while showing strong effects of word frequency with the same stimulus set in a response-limited lexical decision task (Paap & Johansen, 1994). Our simulation results demonstrate that the absence of word frequency effects in the Reicher-Wheeler task can arise in a model where word frequency has an early influence on processing (as opposed to the AV model). We argue that this null effect arises from failing to control for the positional letter (or bigram) frequencies of the different frequency categories (the very high-frequency words had higher positional letter frequencies than the other categories in Paap & Johansen's study). Positional letter frequency reflects the number and frequency of all words that share one letter with the stimulus. Since these one-letter neighbors remain activated only very briefly, they are assumed to be responsible for the observed decrement in performance to very high-frequency targets in data-limited presentation conditions.
GENERAL DISCUSSION
The multiple read-out model of orthographic processing in visual word recognition was submitted to a series of tests against new experimental results (a priori hypothesis testing) in Part I, and previously published data (post-hoc tests of the model) in Part II. The model was successful in all aspects of these tests. In particular, it provided accurate predictions concerning no less than six different dependent variables in a single experiment. In contrast, most models of visual word recognition provide predictions concerning two dependent variables (e.g., correct positive RT, and/or false negative error rate). We consider this a major step forward within the general enterprise of providing a detailed description of the processes and representations involved in recognizing printed words.
Coupling the ∑ (summed lexical activity) and T (time) decision criteria of the multiple read-out model to a single variable computed in early phases of processing allows this model to capture SATO effects in response-limited paradigms. This is the first time that a model of visual word recognition includes precise mechanisms for dealing with these phenomena, rather than adopting the usual strategy of rejecting RT results when a SATO arises. SATO phenomena are part and parcel of speeded RT tasks. Any account of information processing in these tasks must be able to accommodate such phenomena. We have demonstrated that the multiple read-out model achieves this goal with respect to one of the most studied speeded RT tasks in cognitive psychology, the lexical decision task. Moreover, the hypothesized strategic nature of the task-specific ∑ and T criteria allowed the model to provide a unified account of list composition effects (nonword lexicality and frequency blocking) in the lexical decision task.
Clearly, alternative models could be developed to the point that they generate experimental predictions of similar scope and detail. In what follows we shall discuss some of these alternative approaches to modeling visual word recognition in the light of the empirical results used to test the multiple read-out model. Finally, we will examine the limitations of the present approach, and possible directions for the future development of IA models of visual word recognition.
Orthographic Neighborhood Effects and Models of Visual Word Recognition
The majority of the experiments discussed in the present paper examined the effects of orthographic neighborhoods on visual word recognition. With respect to orthographic processing, these results provide the greatest constraints for theoretical development. In particular, we believe that neighborhood effects offer critical evidence in favor of the lexical inhibition hypothesis implemented in IA models of visual word recognition, and stand in contradiction to the lexical independence hypothesis of logogen-type models, and the verification hypothesis of serial search models.
The simulation results discussed in the introduction, pitted a logogen-type model against an IA model of visual word recognition with respect to effects of neighborhood frequency (Grainger & Segui, 1990) and masked orthographic priming (Segui & Grainger, 1990). This comparison was clearly in favor of the IA model, and suggests that the lexical independence hypothesis implemented in logogen-type models cannot accommodate lexical competition effects (Bard, 1990). The verification hypothesis implemented in AV models provides an alternative means of capturing competitor effects in visual word recognition. Thus, AV models that postulate a frequency-ordered verification process (Paap et al., 1982) can accommodate the interfering effects of high-frequency neighbors (Grainger, 1990; Grainger & Segui, 1990; Grainger et al., 1989; 1992). These neighbors will be part of the candidate set generated via stimulus-driven activation, and must therefore be checked and rejected before correct stimulus word identification.
The critical data with respect to a frequency-ordered AV model, however, concerns the effects of number of high-frequency neighbors on performance to low-frequency words. This model clearly predicts that increasing the number of such high-frequency neighbors should increase the number of verification operations necessary before identification, and therefore slow recognition times. The data from Experiment 3 are ambiguous on this point, since inhibitory effects of number of high-frequency neighbors were observed in the progressive demasking task but not in the lexical decision task. Moreover, with a different stimulus set, facilitatory effects of increasing number of high-frequency neighbors have been reported with the progressive demasking task (Grainger, 1992). The dynamics of IA models makes it possible to capture such variations across different stimulus sets. It is not clear how such variations could be captured by AV models. With respect to such variations in effects of orthographic neighborhood across experiments, one interesting area for future investigation concerns the influence of other forms of orthographic similarity between words. For example, one could examine the influence of orthographically similar words of different length (e.g., cart-chart), words that are transposition neighbors (e.g., bale-able), and words differing by more than one letter (e.g., stack-black). Since the interactive activation framework is sensitive to the latter type of influence, this may be one reason why it can simulate apparently contradictory data patterns.
The multiple read-out model uses two distinct mechanisms to account for the influences of orthographic neighbors on performance in the lexical decision task: 1) The inhibitory influences of simultaneously activated word units affects the time taken by a given word unit to reach the M threshold (this follows from the lexical inhibition hypothesis implemented in the model); and 2) the sum of word unit activation (
s or general lexical activity) in early phases of processing influences the relative involvement of the ∑ and the T decision criteria in the model. It is hypothesized that neighborhood frequency and neighborhood density effects in the lexical decision task result from the combined operation of these mechanisms. What distinguishes these two effects is the relative weight given to each mechanism in determining the outcome. Neighborhood frequency differentiates words mainly in terms of the amount of lexical inhibition that they generate (1st mechanism). Neighborhood density differentiates words mainly in terms of the total lexical activity that they generate (2nd mechanism). In other words, the inhibitory effects of a single high-frequency neighbor on the recognition of low-frequency word targets is principally due to the first mechanism. The facilitatory effects of number of neighbors on performance to both word and nonword stimuli in the lexical decision task is principally due to the second mechanism.Inhibitory effects of neighborhood frequency are also found in other measures of word recognition performance such as progressive demasking RTs (Experiment 1; Grainger & Segui, 1990), eye gaze durations on isolated words (Grainger et al., 1989), and percent correct identification in data-limited presentation conditions (Experiment 3). It is hypothesized that the dependent measures in all of these tasks essentially reflect the operation of the M decision criterion. On the other hand, since the ∑ decision criterion is hypothesized to be operational only in the lexical decision task, this accounts for why facilitatory effects of neighborhood density become inhibitory in perceptual identification tasks (Carreiras, Perea, & Grainger, submitted; Snodgrass & Mintzer, 1993; Van Heuven et al., submitted; Ziegler et al., submitted). Also, conditions that are hypothesized to increase the use made of the ∑ decision criterion in the lexical decision task (reduced nonword lexicality and stressing speed over accuracy in the instructions given to subjects) were shown to increase the facilitatory effects of neighborhood density (see also, Andrews, 1989; Johnson & Pugh, 1994) and decrease the inhibitory effects of neighborhood frequency in Experiment 1.
One other point of interest concerns the effects of increasing the number of high-frequency neighbors of low-frequency word stimuli (see Experiment 1; Grainger et al., 1989; Grainger, 1990; 1992). Words with many high-frequency neighbors will often produce higher levels of lexical activity during processing, which will generally result in increased levels of lexical inhibition (compared to words with fewer high-frequency neighbors). This is not, however, a general rule, because simultaneously activated word units mutually inhibit each other in the interactive activation framework. The target word may therefore suffer less lexical inhibition compared to words with fewer neighbors. As noted above, this has been demonstrated in a study reported by Grainger (1992) in which increasing the number of high-frequency neighbors of low-frequency, 4-letter French words actually produced a facilitatory effect on progressive demasking RTs and lexical decision false negative error rate. Moreover, a trend toward a facilitatory effect of number of high-frequency neighbors was also observed by Grainger et al. (1989) in the gaze duration data. This is clearly a critical point for further empirical investigation.
In the multiple read-out model, variations in
s values correctly predicted the pattern of RTs and false positive error rates to nonwords as a function of the number of high-frequency word neighbors. The model correctly predicted a facilitatory effect of increasing numbers of high-frequency word neighbors of nonword stimuli. This result should be difficult for any AV type model to handle. In this respect, the present set of experimental and simulation results are clearly favorable to the lexical inhibition hypothesis of IA models in general. More specifically, they support the particular implementation of a multiple read-out IA model of orthographic processing presented here.Finally, in some recent simulation work the core assumptions of the multiple read-out model (lexical inhibition, noisy decision criteria) have been successfully applied to explain cross-language orthographic neighborhood effects in bilingual subjects (Van Heuven et al., submitted). One of the particularly interesting aspects of this work is that summed lexical activity is considered as part of the core processes of the model and no longer simply a task-specific (lexical decision) component. In this model (the BIA-model), the summed activity of all word units in a given language is used as an index of the likelihood that the stimulus word belongs to that language. This information is used to reduce activity (and hence potential interference) in the non-target language (this is actually achieved by "language nodes" whose activation levels are a function of the
s values in each language, and who send inhibition to all word nodes in the other language). This model does a very good job in capturing the inhibitory effect that is observed when a target word has more orthographic neighbors in the non-target language than in the target language (Van Heuven et al., 1995).Word Frequency Effects
One of the most critical aspects of the AV model (Paap et al., 1982) is that word frequency exerts an influence uniquely during the verification phase. Dobbs et al., (1985) presented data inconsistent with this claim (see also Allen et al., 1992). They manipulated word frequency and target exposure duration and obtained significant effects of word frequency with stimulus exposures and masking conditions that should, according to Paap et al. (1982), prevent verification. Since verification should not have occurred in these conditions, no effect of word frequency was expected (but see Paap & Johansen, 1994, for a critique of these experiments). A similar problem with frequency-ordered AV models has been pointed out by Grainger and Segui (1990). Such models predict a null effect of word frequency when the number of more frequent neighbors is carefully controlled. This follows from the fact that word frequency effects are nothing other than neighborhood frequency effects in such models. It is not absolute word frequency, but the relative frequencies of all candidate words that affects the verification order. However, Experiment 3 in Part 1 of the present study (see also Grainger, 1990; Grainger & Segui, 1990) demonstrated clear word frequency effects in conditions where neighborhood frequency was carefully controlled.
For AV models to be saved, a mechanism must be added that allows word frequency effects to arise prior to verification. This can be achieved by assuming that the resting level activation of word units vary as a function of word frequency (as in IA models), and that the verification stage is ordered by word activation level rather than word frequency. Verification would be initiated once a critical activation level is reached and the verification order would be determined by the order in which word units reach this critical activation level. This modified AV model could then capture the effects of word frequency obtained with short stimulus exposures (Allen et al., 1992; Dobbs et al., 1985), and when neighborhood frequency is controlled. Moreover, such a modification to AV models allows them to accommodate the inhibitory effects of masked orthographically related primes (Segui & Grainger, 1990). On prime presentation, the word unit corresponding to the prime is preactivated, thus increasing the likelihood that this word reach the verification threshold before the target word. This will result in slower target recognition times. Since word frequency influences the time to reach the verification threshold, the modified AV model correctly predicts that this factor will interact with the effects of orthographic priming.
Nevertheless, the modified AV model still has difficulty in handling the results of the experiments reported here. The model captures the inhibitory effects of neighborhood density on nonword decision latencies (Andrews, 1989; Coltheart et al., 1977) by variations in the total number of verifications computed before a "no" response is generated. However, it cannot explain the facilitatory effects of neighborhood frequency on correct negative RT reported in the present article. In Experiment 2, RTs were faster to nonword stimuli with more high-frequency neighbors. The modified AV model predicts the opposite result. The more frequent the word neighbor of a nonword stimulus is, the more likely it will reach critical activation levels for verification, thus slowing the rejection process for the nonword stimulus. Of course, the original AV model simply predicts an inhibitory effect of number of neighbors independently of their frequency.
One of the challenges for IA models of visual word recognition, as pointed out by Paap et al. (1982), is that word frequency effects are rather elusive in the Reicher-Wheeler task. In the IA framework, word frequency is coded in terms of the resting level activations of word units. High frequency words have higher resting level activations than low-frequency words. Thus, word frequency should exert its influence right from the start of the word recognition process, independently of stimulus exposure duration. In our previous work on this topic (Grainger & Jacobs, 1994), we isolated two potential reasons for this. We noted that forced-choice methodology cuts effects sizes in half, and that read-out from the letter level can reduce the influence of word level information on performance in this paradigm. In the present work, we suggest that positional letter frequency (and the highly correlated measure of positional bigram frequency) may also be responsible for the so-called "vanishing frequency effect" discussed by Paap and Johansen (1994). The positional letter frequency of a given word indexes the number and printed frequencies (i.e., a token rather than a type count) of all words of the same length that share one letter in the correct position with the target. Within the framework of IA models, one can consider the N-metric and positional letter frequency as the two extremes of a continuum representing orthographic overlap. In initial cycles of processing in the model, all words that share a single letter with the stimulus will receive some excitatory input. The activity of these single-letter neighbors will, however, very rapidly be inhibited by the much more strongly activated representations corresponding to the stimulus word itself and its full orthographic neighbors. Nevertheless, if the number and the printed frequency of these low-order neighbors (indexed by measures such as positional letter and bigram frequency) are high enough, they can exert a short-lived inhibition on the target word's representation. Since word frequency is positively correlated with positional letter and bigram frequency, this can explain why word frequency effects are so elusive with brief stimulus exposures.
Variations in the size of word frequency effects can also arise as a result of a failure to control for the orthographic neighbors of target words (Monsell, Doyle, & Haggard, 1989; Grainger, 1990). Low-frequency words tend to be more sensitive to the influence of orthographic neighbors than high-frequency words (see the present Experiment 3 for example). Since the influence of orthographic neighbors can either be facilitatory or inhibitory depending on the experimental task, then the difference in performance to low and high-frequency targets can either be diminished or exaggerated by such extraneous influences. This is explained within the framework of the multiple read-out model in terms of the different influences that orthographic neighbors can have on task-specific processes. In the present study, we have shown how performance in a lexical decision task can be facilitated by high neighborhood densities via the task-specific ∑ criterion. The specific processes involved in generating a speeded articulatory response or semantic category judgment to a given target word, may also be influenced by the target's orthographic neighborhood (e.g., Jared, McRae, & Seidenberg, 1990), thus influencing the effects of word frequency observed in these paradigms (Balota & Chumbley, 1984; 1985). However, a complete understanding of the variations in the effects of word frequency, and other variables, across these different tasks, will be achieved only when we can specify exactly how such tasks are performed, and how these task-specific processes relate to a general model of visual word recognition and reading.
Word frequency effects vary not only across different tasks, but also as a function of list context within a given task. In the lexical decision task, word frequency effects increase when the frequency categories are blocked in separate lists compared to mixed presentation (the frequency blocking phenomenon), and they diminish as nonword lexicality decreases (e.g., Stone & Van Orden, 1993). In the multiple read-out model, certain task-specific processes are hypothesized to be strategically variable; they can be adjusted on-line during an experiment as a function of task demands and the stimuli encountered. These adjustments of strategically variable response criteria allow the model to accurately simulate effects of frequency blocking and nonword lexicality in the lexical decision task. Moreover, the fact that variations in the ∑ and T criteria are coupled to the same measure of overall lexical activity in the model allowed it to capture SATO phenomena in lexical decision that have proved particularly problematical for alternative accounts (Balota & Chumbley, 1984; Seidenberg & McClelland, 1989; Stone & Van Orden, 1993). On this point, it is also interesting to note that simulations run with only the ∑ and T criteria could not capture the overall pattern of results. The criterion set on word unit activity (M) is necessary for the successful performance of the multiple read-out model applied to the lexical decision task. This is nicely illustrated in Figure A2 of the appendix where it can be seen immediately that a positive lexical decision response based on the ∑ criterion alone would generate either too many false positive errors or too many false negative errors depending on where the criterion is set (see Besner, Twilley, McCann, & Seergobin, 1990, for a similar criticism of Seidenberg & McClelland's account of lexical decision).
Finally, since the multiple read-out model's account of neighborhood density and frequency blocking effects in the lexical decision task both involve variations in the use made of the ∑ decision criterion, it follows that the model predicts the existence of a density blocking effect that is analogous to the frequency blocking effect. In other words, the facilitatory effects of neighborhood density should increase as a function of the proportion of high density words in the experimental list (with word frequency and type of nonword held constant). This is an easily testable prediction for future experimentation.
Conclusions
The multiple read-out model of visual word recognition provides an integrative framework for explaining a variety of experimental results obtained in both response-limited and data-limited paradigms. With respect to the Venn Diagram presented in Figure 1, we believe that the model provides a promising description of the sections that are specific to the lexical decision task and the perceptual identification task, as well as the intersection between these two. Future tests of this model will include the go/no-go lexical decision task, which represents an intermediate case (M and ∑ criteria), lying in between the perceptual identification task (M criterion only), and the binary lexical decision task (M, ∑, and T criteria). Future developments of the model will concentrate on the third principal task used in studies of visual word recognition, the word naming task, and to this end involve the implementation of phonological representations. The general principle of multiple, noisy decision criteria as embodied in the multiple read-out model, will allow us to provide precise quantitative predictions with respect to percentage errors, RT means and distributions, and strategic influences, on the speeded reading aloud of printed words.
Thus, the further development of algorithmic models of visual word recognition and reading, that clarify the distinction between task-specific and task-independent processes, remains a major goal for this field. Experimental psychologists measure participants' performance in laboratory tasks that have been designed to be as direct a reflection as possible of the psychological process(es) they wish to investigate. Although there is merit in attempting to reduce the gap between laboratory tasks and the natural processes under investigation, we argue that developing our understanding of the functional overlap between the two is a fruitful complement (Jacobs, 1994; Jacobs & Grainger, 1994). Another major aim for future developments consists in trying to bridge the gap between algorithmic models of word recognition and the data arising from a rapidly increasing number of studies using brain imaging techniques (Jacobs & Grainger, 1994; Jacobs & Carr, 1995).
We would like to emphasize another aspect of the modeling strategy adopted here. This concerns the rules used to modify parameters in algorithmic models. We distinguish non-modifiable parameters that form the core of a model, from strategically modifiable parameters involved in task-specific decision mechanisms. The modification of these strategically variable parameters is done in a psychologically plausible and experimentally testable way, that provides a transparent link between how participants might react to changes in the stimulus and task environment, and how the model is made to react to such changes. Any algorithmic model must make this distinction. Once a model's core parameters have been fit to a given set of data, future tests of the model should, in principle, only involve changes to the strategically modifiable parameters (unless, of course, independent motivations compel a parameter change).
Finally, with respect to the ongoing debate between symbolic and sub-symbolic approaches to modeling visual word recognition (among other cognitive activities), the multiple read-out model can be thought of as lying between the two extremes of under-representation (e.g., Seidenberg & McClelland, 1989) and over-representation (e.g., Forster & Taft, 1994). Our model is a member of the symbolic connectionist family that achieves a good balance between the explanatory power provided by representations on the one hand, and processing on the other.
REFERENCES
Allen, P. A., McNeal, M., & Kvak, D. (1992). Perhaps the lexicon is coded as a function of word frequency. Journal of Memory and Language, 31, 826-844.
Andrews, S. (1989). Frequency and neighborhood size effects on lexical access: Activation or search? Journal of Experimental Psychology: Learning, Memory, and Cognition, 15, 802-814.
Andrews, S. (1992). Frequency and neighborhood effects on lexical access: Lexical similarity or orthographic redundancy? Journal of Experimental Psychology: Learning, Memory, and Cognition, 18, 234-254.
Atkinson, R.C. & Juola, J.F. (1973). Factors influencing speed and accuracy of word recognition. In S. Kornblum (Ed.), Attention and Performance IV (pp. 583-612). New York: Academic Press.
Balota, D. A., & Chumbley, J. I. (1984). Are lexical decisions a good measure of lexical access ? The role of word frequency in the neglected decision stage. Journal of Experimental Psychology: Human Perception and Performance, 10, 340-357.
Balota, D. A., & Chumbley, J. I. (1985). The locus of word frequency effects in the pronunciation task: Lexical access and/or production? Journal of Memory and Language, 24, 89-106.
Bard, E.G. (1990). Competition, lateral inhibition, and frequency: Comments of the chapters of Frauenfelder and Peeters, Marslen-Wilson, and others. In G.T.M. Altmann (Ed.), Cognitive Models of Speech Processing: Psycholinguistic and Computational Perspectives (pp. 185-210). Cambridge MA: MIT Press.
Berg, T. & Schade, U. (1992). The role of inhibition in a spreading-activation model of language production. Part I: The psycholinguistic perspective. Journal of Psycholinguistic Research , 21, 405-434.
Besner, D. & McCann, R.S. (1987). Word frequency and pattern distortion in visual word identification and production: An examination of four classed of models. In M. Coltheart (Ed.), Attention and Performance XII (pp. 201-220), Hillsdale NJ: Erlbaum.
Besner, D., Twilley, L., McCann, R., & Seergobin, K. (1990). On the connection between connectionism and data: Are a few words necessary? Psychological Review, 97, 432-446.
Carpenter, R.H.S., & Williams, M.L.L. (1981). Neural computation of log likelihood in control of saccadic eye movements. Nature, 377, 59-62.
Carr, T.H. (1986). Perceiving visible language. In K.R. Boff, L. Kaufman & J.P. Thomas (Eds.), Handbook of perception and human performance (pp. 29.1-29.82), N.Y.: Wiley.
Carr, T.H. & Pollatsek, A. (1985). Recognizing printed words: A look at current models. In D. Besner, T.G. Waller, and G.E. MacKinnon (Eds.) Reading research: Advances in theory and practice 5 (pp. 1-82). San Diego, Ca: Academic Press.
Carreiras, M., Perea, M., & Grainger, J. Effects of Orthographic Neighborhood in Visual Word Recognition: Cross Task Comparisons. Manuscript submitted for publication.
Coltheart, M., Davelaar, E., Jonasson, J. T., & Besner, D. (1977). Access to the internal lexicon. In S. Dornic (ed.), Attention and Performance VI. London: Academic Press.
Coltheart, M. Curtis, B, Atkins, P. & Haller, M. (1993). Models of reading aloud: Dual-route and parallel-distributed-processing approaches. Psychological Review, 100, 589-608.
Coltheart, M. & Rastle, K. (1994). Serial processing in reading aloud: Evidence for dual-route models of reading. Journal of Experimental Psychology: Human Perception and Performance, 20, 1197-1211.
Compton, P., Grossenbacher, P., Posner, M. I., & Tucker, D. M. (1991). A cognitive anatomical approach to attention in lexical access. Journal of Cognitive Neuroscience, 3, 304312.
Den Heyer, K., Goring, A., Gorgichuk, S., Richards, L., & Landry, M. (1988). Are lexical decisions a good measure of lexical access? Repetition blocking suggests the affirmative. Canadian Journal of Psychology, 42, 274-296.
Dobbs, A.R., Friedman, A., & Lloyd, J. (1985). Frequency effects in lexical decisions: A test of the verification model. Journal of Experimental Psychology: Human Perception and Performance, 11, 81-92.
Donnenwerth-Nolan, S., Tanenhaus, M.K., & Seidenberg, M.S. (1981). Multiple code activation in word recognition: Evidence from rhyme monitoring. Journal of Experimental Psychology: Learning, Memory, and Cognition, 7, 170-180
Dorfman, D. & Glanzer, M. (1988). List composition effects in lexical decision and recognition memory. Journal of Memory and Language, 27, 633-648.
Eberhard, K. M. (1994). Phonological inhibition in speech perception. In: D. Dagenbach & T. H. Carr (Eds.), Inhibitory mechanisms in attention, memory, and language (pp. 383-406), San Diego, CA: Academic Press.
Estes, W. K. (1975). Some targets for mathematical psychology. Journal of Mathematical Psychology, 12, 263-282.
Estes, W. K. (1988). Toward a framework for combining connectionist and symbol-processing models. Journal of Memory and Language, 27, 196-212.
Ferrand, L., & Grainger, J. (1992). Phonology and orthography in visual word recognition: evidence from masked nonword priming. Quarterly Journal of Experimental Psychology, 33A, 325-350.
Ferrand, L., & Grainger, J. (1993). The time-course of orthographic and phonological code activation in the early phases of visual word recognition. Bulletin of the Psychonomic Society, 31, 119-122.
Feustel, T.C., Shiffrin, R.M., & Salasoo, A. (1983). Episodic and lexical contributions to the repetition effect in word identification. Journal of Experimental Psychology: General, 112, 309-346.
Forster, K.I. (1992). Memory-addressing mechanisms and lexical access. In R. Frost and L. Katz (Eds.). Orthography, Phonology, Morphology, and Meaning (pp. 413-434). Amsterdam: North Holland.
Forster, K. I., & Davis, C. (1984). Repetition priming and frequency attenuation in lexical access. Journal of Experimental Psychology: Learning, Memory, and Cognition, 10, 680-690.
Forster, K.I. & Taft, M. (1994). Bodies, antibodies, and neighborhood density effects in masked form priming. Journal of Experimental Psychology: Learning, Memory, and Cognition, 20, 844-865.
Frauenfelder, U.H. & Peters, G. (1990). Lexical segmentation in TRACE: An exercise in simulation. In G.T.M Altmann (Ed.), Cognitive Models of Speech Processing: Psycholinguistic and Computational Perspectives (pp. 50-86). Cambridge MA: MIT, Press.
Frauenfelder, U., & Peeters, G. (1994). Simulating the time-course of word recognition: An analysis of lexical competition in TRACE. Journal of Memory & Language, in press.
Glanzer, M. & Ehrenreich, S.L. (1979). Structure and search of the internal lexicon. Journal of Verbal Learning and Verbal Behavior, 18, 381-398.
Goldinger, S.D., Luce, P.A., & Pisoni, D.B. (1989). Priming lexical neighbors of spoken words: Effects of competition and inhibition. Journal of Memory & Language, 28, 501-518.
Goldinger, S.D., Luce, P.A., Pisoni, D.B., & Marcario, J.K. (1992). Form-based priming in spoken word recognition: The roles of competition and bias. Journal of Experimental Psychology: Learning, Memory, and Cognition, 18, 1211-1238.
Gordon, B. (1983). Lexical access and lexical decision: Mechanisms of frequency sensitivity. Journal of Verbal Learning and Verbal Behavior, 22, 24-44.
Grainger, J. (1990). Word frequency and neighborhood frequency effects in lexical decision and naming. Journal of Memory & Language, 29, 228-244.
Grainger, J. (1992). Orthographic neighborhoods and visual word recognition. In R. Frost and L. Katz (Eds.). Orthography, Phonology, Morphology, and Meaning (pp. 131-146). Amsterdam: North Holland.
Grainger, J., & Jacobs, A. M. (1993). Masked partial-word priming in visual word recognition: Effects of positional letter frequency. Journal of Experimental Psychology: Human Perception and Performance, 19, 951-964.
Grainger, J., & Jacobs, A. M. (1994). A dual read-out model of word context effects in letter perception: Further investigations of the word superiority effect. Journal of Experimental Psychology: Human Perception and Performance, 20, 1158-1176.
Grainger, J., O'Regan, J. K., Jacobs, A. M. & Segui, J. (1989). On the role of competing word units in visual word recognition: The neighborhood frequency effect. Perception & Psychophysics, 45, 189-195.
Grainger, J., O'Regan, J. K., Jacobs, A. M., & Segui, J. (1992). Neighborhood frequency effects and letter visibility in visual word recognition. Perception & Psychophysics, 51, 49-56.
Grainger, J. & Segui, J. (1990). Neighborhood frequency effects in visual word recognition: A comparison of lexical decision and masked identification latencies. Perception & Psychophysics, 47, 191-198
Green, D.M. & Swets, J.A. (1966). Signal detection theory and psychophysics. New York: Wiley.
Grice, G.R. (1968). Stimulus intensity and response evocation.
Psychological Review, 75, 359-373.
Grice, G. R., Nullmeyer, R., & Spiker, V. A. (1982). Human reaction time: toward a general theory. Journal of Experimental Psychology: General, 111, 135-153.
Günther, H., Gfroerer, S., , & Weiss, L., (1984). Inflection, frequency, and the word superiority effect. Psychological Research, 46, 261-281.
Hawkins, H.I., Reicher, G.M., Rogers, M., & Peterson, I. (1976).Flexible coding in word recognition. Journal of Experimental Psychology: Human Perception and Performance, 2, 380-385.
Imbs, P. (1971). Etudes statistiques sur le vocabulaire français. Dictionnaire des fréquences. Vocabulaire littéraire des XIXe et XXe siècles. Centre de recherche pour un trésor de la langue française (CNRS) Nancy. Paris: Librairie Marcel Didier.
Jacobs, A. M. (1993). Modeling the effects of visual factors on saccade latency. In G. d'Ydewalle & J. van Rensbergen (Eds.), Perception & Cognition: Advances in eye movement research, (pp. 349 - 361). Amsterdam: North-Holland.
Jacobs, A. M. (1994). On computational theories and multilevel, multitask models of cognition: The case of word recognition. Behavioral and Brain Sciences, 17, 670-672.
Jacobs, A. M., & Carr, T. H. (1995). Mind mappers and cognitive modelers: Toward cross-fertilization. Behavioral and Brain Sciences, 18, 362-363.
Jacobs, A.M. & Grainger, J. (1991). Automatic letter priming in an alphabetic decision task. Perception and Psychophysics, 49, 43-52.
Jacobs, A.M. & Grainger, J. (1992). Testing a semistochastic variant of the interactive activation model in different word recognition experiments. Journal of Experimental Psychology: Human Perception and Performance, 18, 1174-1188.
Jacobs, A.M. & Grainger, J. (1994). Models of visual word recognition - Sampling the state of the art. Journal of Experimental Psychology: Human Perception and Performance, 20, 1311-1334.
Jared, D., McRae, K., & Seidenberg, M.S. (1990). The basis of consistency effects in word naming. Journal of Memory and Language, 29, 687-715.
Johnson, N.F. & Pugh, K.R. (1994). A cohort model of visual word recognition. Cognitive Psychology, 26, 240-346.
Jonides, J., & Mack, R. (1984). On the cost and benefit of cost and benefit. Psychological Bulletin, 96, 29-44.
Kosslyn, S. M., & Intrilligator, J. M. (1992). Is cognitive neuropsychology plausible ? The perils of sitting on a one-legged stool. Journal of Cognitive Neuroscience, 4, 96-106.
Krueger, L. E. (1978). A theory of perceptual matching. Psychological Review, 85, 278-304.
Kuçera, H. & Francis, W.N. (1967). Computational analysis of present-day American English. Providence, RI: Brown University Press.
Luce, R. D. (1986). Response times. Oxford University Press.
Lukatela, G., Lukatela, K., & Turvey, M.T. (1993). Further evidence for phonological constraints on visual lexical access: TOWED primes FROG. Perception and Psychophysics, 53, 461-466.
Lukatela, G. & Turvey, M.T. (1990). Phonemic similarity effects and prelexical phonology. Memory and Cognition. 18, 128-152.
Marslen-Wilson, W.D. (1987). Functional parallelism in spoken word recognition. Cognition, 25, 71-102.
Marslen-Wilson, W.D. (1990). Activation, competition, and frequency in lexical access. In G.T.M. Altmann (Ed.), Cognitive Models of Speech Processing: Psycholinguistic and Computational Perspectives (pp. 148-172). Cambridge MA: MIT, Press.
Marslen-Wilson, W.D. & Welsh, A. (1978). Processing interactions and lexical access during word recognition in continuous speech. Cognitive Psychology, 10, 29-63.
Marr, D. (1982). Vision. San Francisco: Freeman.
Massaro, D.W. & Cohen, M.M. (1994). Visual, orthographic, phonological, and lexical influences in reading. Journal of Experimental Psychology: Human Perception and Performance, 20, 1107-1128.
Massaro, D. W., & Friedman, D. (1990). Models of integration given multiple sources of information. Psychological Review, 97, 225-252.
McClelland, J. L. (1979). On the time relations of mental processes: an examination of systems of processes in cascade. Psychological Review, 86, 287-330.
McClelland, J. L. (1987). The case for interactionism in language processing. In M. Coltheart (ed.), Attention & Performance XII: The psychology of reading. (pp. 1-35). Hillsdale: Erlbaum.
McClelland, J. L. (1993). Toward a theory of information processing in graded, random, and interactive networks. In: D. E. Meyer & S. Kornblum (eds.), Attention & Performance XIV: Synergys in Experimental Psychology, Artificial Intelligence, and Cognitive Neuroscience (pp. 655-688). Cambridge, MA: MIT Press.
McClelland, J. L. & Elman, J. L. (1986). The TRACE model of speech perception. Cognitive Psychology, 18, 1-86.
McClelland, J. L. & Rumelhart, D. E. (1981). An interactive activation model of context effects in letter perception: Part I. An account of basic findings. Psychological Review, 88, 375-407.
McClelland, J. L. & Rumelhart, D. E. (1988). Parallel distributed processing: Explorations in the microstructure of cognition (Vol. 3). Cambridge, MA: Bradford Books.
McQueen, J.M., Norris, D, & Cutler, A. (1994). Competition in spoken word recognition: Spotting words in other words. Journal of Experimental Psychology: Learning, Memory, and Cognition, 20, 621-638.
Mewhort, D. J. K., Braun, J. G., & Heathcote, A. (1992). Response time distributions and the stroop task: A test of the Cohen, Dunbar, and McClelland (1990) model. Journal of Experimental Psychology: Human Perception and Performance, 18, 872-882.
Meyer, D. E., Irwin, D. E., Osman, A. M., & Kounios, J. (1988). The dynamics of cognition and action: mental processes inferred from speed-accuracy decomposition. Psychological Review, 95, 183-237.
Monsell, S. (1991). The nature and locus of word frequency effects in reading. In D. Besner and G.W. Humphreys (Eds.), Basic Processes in Reading: Visual Word Recognition (pp. 148-197). Hillsdale NJ: Erlbaum.
Monsell, S., Doyle, M.C., & Haggard, P.N. (1989). Effects of frequency on visual word recognition tasks: Where are they ? Journal of Experimental Psychology: General, 118, 43-71.
Morton, J. (1969). Interaction of information in word recognition. Psychological Review, 76, 165-178.
Murdock, B.B. & Dufty, P.O. (1972). Strength theory and recognition memory. Journal of Experimental Psychology, 94, 284-290.
Nazir, T. A., & Jacobs, A. M. (1991). Effects of target discriminability and retinal eccentricity on saccade latencies: an analysis in terms of variable criterion theory. Psychological Research / Psychologische Forschung, 53, 281-289.
Norris, D.G. (1994). A quantitative model of reading aloud. Journal of Experimental Psychology: Human Perception & Performance, 20, 1212-1232.
O'Regan, J. K., & Jacobs, A. M. (1992). Optimal viewing position effect in word recognition: A challenge to current theory. Journal of Experimental Psychology: Human Perception & Performance, 18, 185-197.
Paap, K., & Johansen, L. (1994). The case of the vanishing frequency effect: A retest of the verification model. Journal of Experimental Psychology: Human Perception & Performance, 20, 1129-1157.
Paap, K., McDonald, J.E., Schvaneveldt, R.W., & Noel, R.W. (1987). Frequency and pronounceablity in visually presented naming and lexical decision tasks. In M. Coltheart (Ed.), Attention and Performance XII (pp. 221-244), Hillsdale NJ: Erlbaum.
Paap, K., Newsome, S. L., McDonald, J. E., & Schvaneveldt, R. W. (1982). An activation-verification model for letter and word recognition: The word superiority effect. Psychological Review, 89, 573-594.
Pachella, R. G. (1974). An interpretation of reaction time in information processing research. In: B. Kantowitz (Ed.), Human information processing: Tutorials in performance and cognition. Hillsdale, N. J.: Erlbaum.
Perfetti, C.A., & Bell, L. (1991). Phonemic activation during the first 40 ms of word identification: Evidence from backward masking and priming. Journal of Memory and Language, 30, 473-485.
Posner, M. I., & Carr, T. H. (1992). Lexical access and the brain: anatomical constraints on cognitive models of word recognition. American Journal of Psychology, 105, 1-26.
Posner, M. I., & McCandliss, B. D. (1993). Converging methods for investigating lexical access. Psychological Science, 4, 305-309.
Pugh, K. R., Rexer, K., Peter, M., & Katz, L. (1994). Neighborhood effects in visual word recognition: Effects of letter delay and nonword context difficulty. Journal of Experimental Psychology: Learning, Memory, and Cognition, 20, 639-648.
Ratcliff, R. (1978). A theory of memory retrieval. Psychological Review, 85, 59-108.
Ratcliff, R. & Murdock, B.B. (1976). Retrieval processes in recognition memory. Psychological Review, 83, 190-214.
Ratcliff, R. & Van Zandt, T. (1995). Comparing connectionist and diffusion models of reaction time. Manuscript submitted for publication.
Reicher, G. M. (1969). Perceptual recognition as a function of meaningfulness of stimulus material. Journal of Experimental Psychology, 81, 274-280.
Roberts, S., & Sternberg, S. (1993). The meaning of additive reaction-time effects: Tests of three alternatives. In: D. E. Meyer & S. Kornblum (Eds.), Attention & Performance XIV: Synergys in Experimental Psychology, Artificial Intelligence, and Cognitive Neuroscience (pp. 611-653). Cambridge, MA: MIT Press.
Rumelhart, D. E., & McClelland, J. L. (1982). An interactive activation model of context effects in letter perception: Part II. The contextual enhancement effect and some tests and extensions of the model. Psychological Review, 89, 60-94.
Schade, U. & Berg, T. (1992). The role of inhibition in a spreading-activation model of language production. Part II: The simulation perspective. Journal of Psycholinguistic Research , 21, 435-462.
Sears, C.R., Hino, Y. & Lupker, S.J. (1995). Neighborhood size and neighborhood frequency effects in word recognition. Journal of Experimental Psychology: Human Perception & Performance, 21,876-900.
Seidenberg, M. S. & McClelland, J. L. (1989). A distributed, developmental model of word recognition and naming. Psychological Review, 96, 523-568.
Segui, J., & Grainger, J. (1990). Priming word recognition with orthographic neighbors: effects of relative prime-target frequency. Journal of Experimental Psychology: Human Perception & Performance, 16, 65-76.
Snodgrass, J.G. & Mintzer, M. (1993). Neighborhood effects in visual word recognition: Facilitatory or inhibitory? Memory and Cognition, 21, 247-266.
Sternberg, S. (1966). High speed scanning in human memory. Science, 153, 652-654.
Stone, G.O. & Van Orden, G.C. (1993). Strategic control of processing in word recognition. Journal of Experimental Psychology: Human Perception & Performance, 19, 744-774.
Stone, G. O., & Van Orden, G. C. (1994). Building a resonance framework for word recognition using design principles and system principles. Journal of Experimental Psychology: Human Perception and Performance, 20, 1248-1268.
Van Heuven, W.J.B., Dijkstra, T. & Grainger, J. Orthographic neighborhood effects in bilingual word recognition. Manuscript submitted for publication.
Van Zandt, T., & Ratcliff, R. (1995). Statistical mimicking of reaction time data: single-process models, parameter variability, and mixtures. Psychological Bulletin & Review, 2, 20-54.
Waters, G.S. & Seidenberg, M.S. (1985). Spelling-sound effects in reading: Time course and decision criteria. Memory and Cognition, 13, 557-572.
Wheeler, D.D. (1970). Processes in word recognition. Cognitive Psychology, 1, 59-85.
Ziegler, J.C., & Jacobs, A. M. (1995). Phonological information provides early sources of constraint in the processing of letter strings. Journal of Memory and Language, 34, 567-593.
Ziegler, J.C., Rey, A., & Jacobs, A.M. Quantitative predictions of identification thresholds and serial error functions: New constraints for models of word recognition. Manuscript submitted for publication.
Ziegler, J.C., Van Orden, G.C., & Jacobs, A.M. Phonology can help or hurt the perception of print. Journal of Experimental Psychology: Human Perception and Performance, in press.
AUTHOR NOTES
The groundwork for this article was carried out while the authors were research scientists at the Laboratoire de Psychologie Expérimentale, Centre Henri Piéron, in Paris. We dedicate the present work to this historical center of French Experimental Psychology. The research was supported by a French national research grant "Sciences de la Cognition" awarded to the authors. Parts of this research were reported at the 34th annual meeting of the Psychonomic Society, Washington, 1993, and the 7th conference of the European Society for Cognitive Psychology, Lisbon, 1994. Thanks to Tom Carr, Ken Paap, Greg Stone, Jo Ziegler and two anonymous reviewers for their helpful comments on earlier versions of this article. Fabrice Parpaillon deserves particular credit for his re-programming of the original interactive activation model. Both authors contributed equally to the present work and order is alphabetical. The authors can be contacted at: Grainger@romarin.univ-aix.fr or Jacobs@lnf.cnrs-mrs.fr
APPENDIX
The implemented model
The interactive activation (IA) model described in McClelland and Rumelhart (1981) serves as the basic architecture for the present implementation. The original computer program (McClelland & Rumelhart, 1988) was modified in the following respects: 1) Several new decision criteria were added to simulate participants' responses in a variety of word recognition tasks; 2) stochastics were introduced in the model by making the decision criteria vary normally around a mean value
3 (Jacobs & Grainger, 1992); 3) new lexica were constructed (4 and 5-letter French words and 5-letter English words); and 4) a different user interface was implemented to facilitate the running of the large-scale simulations required here (i.e., testing the model using the same number of trials (items X participants) as in a real experiment). Unless otherwise stated, all the original parameter settings of the IA model were maintained in the present simulations.Three response criteria ( M, ∑, and T) were added to this basic framework, one to simulate performance in tasks requiring unique word identification (M), and the two others specifically for simulating performance in the lexical decision task. The M criterion is set on a dimension corresponding to the activation level of the individual word units (referred to as µ). This criterion varies randomly around a mean value but is hypothesized not to be subject to strategic modifications. This response criterion was already implemented in Jacobs and Grainger's (1992) semistochastic interactive activation model (SIAM) and provided accurate descriptions of the means and distributions of RTs in several word recognition experiments.
For the purposes of modeling the lexical decision task two other response criteria were added to the model. The ∑ criterion is set on a dimension corresponding to the sum of activations of all word units (referred to as
s), whereas the T criterion is set on the dimension corresponding to time (t) from stimulus onset (i. e. number of processing cycles). These two criteria vary randomly around a mean value similarly to the M criterion, but unlike M their mean values vary in two important ways:1) On each trial the mean values of these criteria are set as a function of the
s values generated by the stimulus.2) More global (strategic) adjustments of the mean values of these criteria can occur during the course of an experiment as a function of the distribution of
s values of the experimental stimuli and task demands concerning speed and accuracy of response.
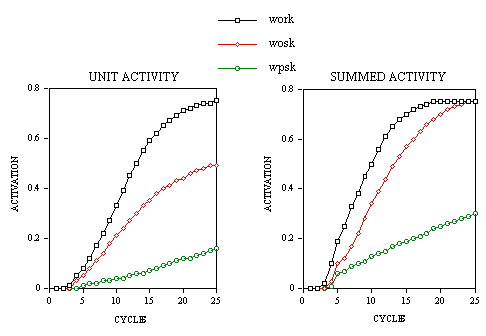
Figure A1. Activation functions for the most activated word unit (local activity or µ) and for the sum of all activated word units (global activity or
s) for an example word, pronounceable nonword, and illegal nonword.
Figure A1 provides examples of how µ and
s vary over time for a word, an orthographically legal, pronounceable nonword, and an illegal nonword. In the case of the nonword stimuli, it is the activation level of the most activated word unit that is shown for µ.For reasons of simplicity we decided to use the
s values computed after 7 cycles of processing, referred to here as s(7), to adjust the ∑ and T criterion on each trial. In our previous simulation work (Jacobs & Grainger, 1992) we had actually used 5 cycles as the critical moment. However, further explorations of the model (notably with different lexica) indicated that 7 cycles proved to be more reliable. Clearly the use of s(7) as the critical value for adjusting the ∑ and T criteria in the model can only be considered a simplifying approximation to what the word recognition system might really be computing. More complex running averages of s values over a larger time slice might be more realistic but pilot simulation work has shown that these are likely to give results not very different from the solution adopted here. The s(7) value computed by the model can be thought of as an index of the likelihood that the stimulus being processed is a word, or alternatively as an index of the word-likeness of the stimulus. If a given stimulus generates lexical activity that lies above certain critical s(7) values then the ∑ and T decision criteria are consequently modified. Thus, the critical values of s(7) used to determine shifts in the ∑ and T criteria are considered free parameters which may vary across experiments according to word/nonword discriminability and task demands relative to speed and accuracy of performance. These critical values can be estimated using the distribution of the s values for the word and nonword stimuli in an experiment and the relative number of false negative and false positive responses observed in experimentation.The algorithm used to adjust the ∑ and T response criteria as a function of
s(7) values simply implements the fact that if overall lexical activity is very low then it is very likely that the stimulus is a nonword, so setting a low temporal threshold is in order. As lexical activity increases then it is more likely that the stimulus is a word and so setting a higher temporal threshold is in order. Very high levels of lexical activity in early stages of processing imply that the stimulus is very likely to be a word so as well as setting a higher T threshold the decision mechanism also adopts a lower ∑ threshold.The simulations of Experiments 1 and 3 used the French 5-letter word lexicon and the simulations of Experiment 2 used the French 4-letter lexicon both previously implemented by Jacobs and Grainger (1992). The M criterion was implemented in the same way as in our previous simulation word. As an example, we provide the mean values of the strategically variable criteria (∑ and T) that were adopted for the simulation of Experiment 1B:
T criterion: if
s(7) > 0.22 then T=22 cycles else T=20 cycles.∑ criterion: if
s(7) > 0.38 then ∑=0.95 else ∑=1.5.Once again the use of a binary decision to adjust the mean values of these two criteria on each trial can only be considered a simplifying first approximation. It may be more plausible to relate the mean criterion values to summed lexical activity values via some continuous function.
Parameter adjustments in the multiple read-out model.
The values used to adjust the ∑ and T criteria varied across the other simulations reported here as a function of the
s values of the stimuli used in the experiment, the relative error rates of participants in the different experiments, and task instructions. Thus, in a certain sense the model has six free parameters that can be adjusted from experiment to experiment. These are not, however, free parameters in the usual sense applied in mathematical modeling. Rather than fitting these parameters using a particular parameter fitting algorithm, here we adopted a procedure that combines theoretically motivated modifications of the parameters followed by a process of fine-tuning.Thus, for example, in Experiment 1 the parameters were adjusted in order to simulate the influence of nonword lexicality (Experiment 1C) and task instructions (Experiment 1D) on neighborhood frequency and neighborhood density effects in the lexical decision task. The multiple read-out model makes specific predictions concerning the way the parameters must be modified in order to capture the effects of nonword lexicality and task demands. The modifications of the parameters were therefore strongly constrained by these theoretical considerations. Moreover, since false positive and false negative error rate is strongly influenced by these parameter settings this imposed a further constraint on the values that could be adopted in order to simulate variations in mean RT. Thus, the only trial-and-error type of tuning that occurred involved relatively slight modifications of the parameter values (fine-tuning) in order to improve the models fit to the finer details of the data. Moreover, it must be underlined that the parameters of the ∑ and T criteria cannot be adjusted to fit any possible data pattern. This would be the case, for example, if two stimulus categories in a hypothetical experiment produced differences in performance not predicted by the M criterion in the model, and that could not be distinguished in terms of the summed lexical activity they generate.
One more important modification involved the simulations with 5-letter word stimuli. We decided to keep the critical
s values within the same range as in the 4-letter lexicon by decreasing the s values generated by 5-letter words. This was done by reducing the letter-word excitation parameter from 0.07 to 0.06 in the present simulation studies. This also brings the asymptotic values of word units in line with those produced by the 4-letter lexicon, and therefore allows us to maintain decision criteria within the same range across the 4 and 5-letter simulations. Reducing the letter-word excitation parameter can be taken to reflect the reduced visibility of letters in words with increasing word length. This reduced visibility can be attributed to increased retinal eccentricity and lateral interactions (O'Regan & Jacobs, 1992). The same reduction in the letter-word excitation parameter was applied to the 5-letter English lexicon used in Simulation Study 3. This lexicon included 2094 words of frequencies ranging from 2 per million to 3562 per million (Kuçera & Francis, 1967). Resting level activations varied as a function of word frequency as in the 4-letter lexicon (Jacobs & Grainger, 1992).
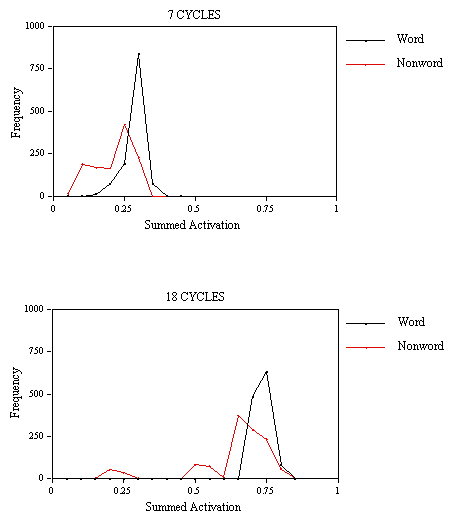
Figure A2. Frequency distribution of the values of summed lexical activity (
s) generated by 1195 English 4-letter words and 1195 orthographically legal, pronounceable 4-letter nonword stimuli after 7 and 18 cycles of processing in the model.
Finally, one interesting question with respect to the multiple read-out model's account of lexical decision, is whether performance in this task could be simulated without the M criterion (i.e., without lexical representations). Figure A2 shows the distribution of
s values at 7 and 18 cycles for the entire English 4-letter word lexicon implemented in the model, and 1195 orthographically legal, pronounceable nonwords of 4 letters in length. The largely overlapping distribution of these values for words and nonwords at 18 cycles (the shortest average positive response times generated by the model) demonstrates that the model could not possibly perform the lexical decision task with the accuracy of human participants if only the S criterion were used for positive responses. This criterion can therefore only be considered a complement to the use of word-specific information in making lexical decisions.