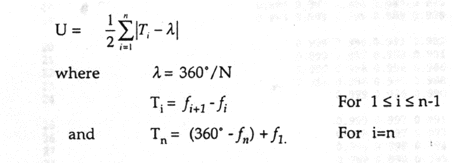
An expanded table of probability values for Rao's Spacing Test Gerald S. Russell Daniel J. Levitin Department of Psychology University of Oregon
This is an electronic Web version of the paper originally appearing in Communications in Statistics: Simulation and Computation, 24(4), 879-888. Copyright 1997 Daniel J. Levitin. Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted with or without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and full citation on the first page. To copy otherwise,to republish, to post on services, or to redistribute to lists, requires specific permission and/or a fee.
Abstract
Rao's Spacing Test is a useful and powerful statistic for testing uniformity with circular and periodic data. Previously published tables of critical values are incomplete, giving critical values only out to p=.1 and n = 200. We extend those tables to n=1000 and for p-values out to 0.9. The extension will enable researchers to better evaluate the confidence with which they are accepting the null hypothesis, and to use the test with larger n.
Introduction
The last decade has seen a marked renewal of interest in circular staitistics, statistical methods employed when the underlying metric of observations is circular or periodic. Examples of circular metrics include time series data, psychophysical measurements of color and musical pitch, and directional measurements of the orienting responses of organisms. With the recent publication of a new monograph on the subject (Fisher, 1993), circular statistics might become more well known and widely used in the years to come.
One particularly useful statistic for testing uniformity of observations is Rao's Spacing Test (Batschelet, 1981; Rao, 1976). In many cases, Rao's test is more powerful than the popular alternatives, such as the Rayleigh Test and Kuiper's V test (Levitin, 1994; Rao, 1972). The test is based on the idea that if the underlying distribution is uniform, successive observations should be approximately evenly spaced, about 360°/N apart. Large deviations from this distribution, resulting from unusually large spaces or unusually short spaces between observations, are evidence for directionality. The test statistic U is defined as:
(1)
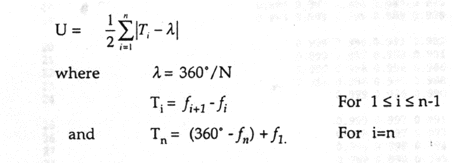
Because the sum of the positive deviations must equal the sum of the negative deviations, a simpler computational form eliminates absolute values, so that
(2)
U = ![]()
summed across positive deviations only.
The density function of U is known to be (Rao, 1976):
(3)
![]()
for ![]()
where 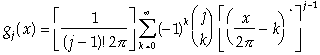
Critical values of the U statistic for p = .01, .05 and .1 and n = 1 to 200 were compiled into a table by Rao (1976) and later reproduced by Batschelet (1982). The complexity of the density function compels all but the most dedicated researchers to rely on published tables. We hope that with the publication of this table more investigators will be able to use the test.
Computational Method
If we let a=x/2pi, then the inner sum in the expression for gj(x) may be written as:
(4)
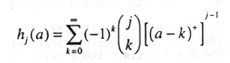
This expression is similar to the expression for Sterling's numbers of the second kind (Bogart, 1990); and like Sterling's numbers, it may be evaluated using a recurrence relation,
(5)
hj(a) - a * hj-1(a) + (j-a) * hj-1(a-1)
For large n, the terms hj(1) become very large. We used arbitrary precision floating point numerics (Press, Teukolsky, Vetterling and Flannery, 1992) to represent the values in the series.
A trapizoidal integration was used to exaluate p given the density function U. The integration was repeated at increasing step sizes until stable values for p were obtained. Finally, a cubic spline interpolation routine was used to find the values shown in the tables below. Table I shows p values for n=4 to n=1000 when the value of the test statistic U is known. Table II the value of the test statistic U when given the parameters n and p, again, for n=4 to n=1000, and for stepped p values between 0.001 and 0.9.
The values we obtained differ slightly in some cases from those obtained by Rao two decades ago. Perhaps this is due to our use of arbitrary precision arithmetic and relatively small step sizes in our calculations, which were made possible by the high speed and large memory capacity of present day computers.
Click here to see the statistical tables.
Examples.
Both example 1 and example 2 were taken from Levitin (1994). Fig. 1 displays hypothetical data for onset time of seizures in an epileptic patient, collected across several weeks. The data form a continuous circular distribution, and times of day are converted into angles around the circle. 0° = 12 midnight; each hour = 360°/24 = 15°; minutes = 15°/60 = .25°. The experimental question is whether the seizures are uniformly distributed throughout the day, or whether there are increased seizures at particular times. The times for seizure onsets are 12:26 am, 1:20 am, 1:31 am, 2:00 am, 3:20 am, 4:40 am, 6:32 am, 7:20 am, 9:20 am, 3:20 pm, 7:20pm, 9:00 pm, 10:00 pm, 11:12 pm, 11:12 pm; the equivalent angular displacements, f, are: 6.5°, 20°, 22.8°, 30°, 50°, 70°, 98°, 110°, 140°, 230°, 290°, 315°, 330°, 348°, 348°. The computations for the Rao test in the epileptic seizure example are shown in Table III. The Rao test yields U=113, p>.74. A Rayleigh test of the same distribution yields p=.033. This result illustrates that the Rao test is not the most porwerful in all cases. In particular, it is less powerful than alternative tests when the distribution is unimodal or multi-modal on a global scale, yet simultaneously very uniform over local regions of the distribution. However, in other cases, Rao's test has greater power than alternatives, as shown in the following example.
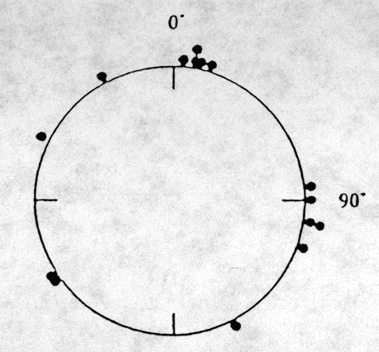
Fig. 2 displays another set of hypothetical data for a different epileptic patient recording the times fo onset of seizures. In this example, the angular values of the times are: 5, 10, 10, 12, 17, 85, 90, 99, 100, 110, 153, 233, 235, 296 and 331. In this case, under Rao's spacing test, we fingd U=177, p<.02. By comparison, the Rayleigh test yields p=.21. The Rao test is more sensitive to the non-uniformity of this distribution because it is more locally "clumpy" than the first example.
Bibliography
Batschelet, E. (1981). Circular statistics in biology. London: Academic Press.
Bogart, K.P. (1990). Introductory Combinatories. (2nd ed.) Orlando, Fl: Harcourt Brace Jovanovich
Fisher, N. I. (1993). Statistical analysis of circular data. Cambridge: Cambridge University Press.
Levitin, D.J. (1994). Limitations of the Kolmogorov-Smirnov statistic: The need for circulat statistics in Psychology. (Tech. Rep. No. 94-7). Eugene, OR: University of Oregon, Institute of Cognitive & Decision Sciences.
Rao, J.S. (1972). Bahadur efficiencies of some tests for uniformity on the circle. Annals of Mathematical Statistics, 43, 468-479.
Rao, J.S. (1976). Some tests based on arc-lengths for the circle. Sankhya: The Indian Journal of Statistics, Ser. B(4), 38, 329-338.
As of 8/1/96, address correspondence to: Daniel Levitin, Behavioral Science Laboratory, Interval Research Corporation , 1801C Page Mill Road, Palo Alto, CA 9430. Phone: (650) 842-6236. E-mail: levitin@interval.com