Levitin, D. J. (1994) Absolute memory for musical pitch: Evidence from the production of learned melodies Perception & Psychophysics, 56 (4), 414-423.
Absolute memory for musical pitch:
Evidence from the production of learned melodies
Daniel J. Levitin
University of Oregon
This is an electronic Web version of the
paper originally appearing in Perception & Psychophysics,
1994, 56 (4), 414-423. Copyright 1997 Daniel J. Levitin. Permission
to make digital or hard copies of part or all of this work for
personal or classroom use is granted with or without fee provided that
copies are not made or distributed for profit or commercial advantage
and that copies bear this notice and full citation on the first
page. To copy otherwise,to republish, to post on services, or to
redistribute to lists, requires specific permission and/or a fee.
Abstract
Evidence for the absolute nature of long-term auditory memory is provided by analyzing the production of familiar melodies. Additionally, a two-component theory of absolute pitch is presented, which conceives of this rare ability as consisting of a more common ability, pitch memory, and a separate, less common ability, pitch labeling. Forty-six subjects sang two different popular songs and their productions were compared to the actual pitches used in recordings of those songs. 40% of the subjects sang the correct pitch on at least one trial; 12% of the subjects hit the correct pitch on both trials, and 44% came within two semitones of the correct pitch on both trials. The results show a convergence with previous studies on the stability of auditory imagery and latent absolute pitch ability; further, the results suggest that individuals might possess representations of pitch that are more stable and accurate than previously recognized.
One form of absolute memory that has received more attention is the study of that small subset of the population who possess Absolute Pitch (AP). By definition, AP is the ability to produce or identify specific pitches without reference to an external standard (Baggaley, 1974). AP possessors have internalized their pitch references, and they are evidently able to maintain stable representations of pitch in long-term memory. AP is regarded as a rare and somewhat mysterious ability, occurring in as few as 1 in 10,000 people (Takeuchi & Hulse, 1993; Profita & Bidder, 1988). From what we know about the auditory system, its rarity is puzzling. Cells that respond to particular frequency bands are found at every level of the auditory system (Bharucha, 1992; Handel, 1989; Kolb & Whishaw, 1990; Moore, 1989; Pierce, 1983). Information about the absolute pitch of a stimulus is therefore potentially available throughout the auditory system. In light of this, the proper question might not be the often asked "why do so few people have AP?" but rather, "why doesn't everybody?"
Perhaps everybody does have AP to some extent. A growing body of empirical evidence suggests that people who might not be classified as "traditional" AP possessors may nevertheless possess abilities resembling absolute pitch. For example, non-AP subjects asked to identify the pitch of a tone do perform better than chance, and their errors approximate a normal distribution around the correct tone (Lockhead & Byrd, 1981). Similar findings were reported for musically trained subjects asked to identify the musical key of a composition (Terhardt & Seewan, 1983; Terhardt & Ward, 1982).
Even non-musicians seem to possess something similar to absolute pitch. Deutsch and her colleagues found this while investigating two aspects of music cognition: invariance of tonal relations under transposition, and the dimensionality of internal pitch representations (Deutsch, 1991, 1992; Deutsch, Kuyper & Fisher, 1987). In these studies, subjects were asked to judge the height of modified Shepard tones (Shepard, 1964). A pair of such tones, with their focal frequency a tritone apart, form a sort of auditory necker cube and are ambiguous as to whether the second tone is higher or lower than the first. Subjects' directional judgments were found to be dependent on pitch class, leading Deutsch to conclude that, although her subjects were not able to label the tones, they were nevertheless using AP indirectly. Deutsch further speculated that absolute pitch "is a complex faculty which may frequently be present in partial form" (Deutsch, Moore and Dolson, 1986, p. 1351).
Taken together, these studies suggest that AP is neither an isolated and mysterious ability, nor a sign of unusual musical endowment; it is perhaps merely a small extension to memory abilities that are widespread in the general population. One way to make sense of this evidence is to posit that AP consists of two distinct component abilities: (1) The ability to maintain stable, long-term representations of specific pitches in memory, and to access them when required (pitch memory); and (2) the ability to attach meaningful labels to these pitches, such as C#, A440 or Do (pitch labeling). Whereas "true" AP possessors have both abilities, pitch memory might be widespread among ordinary people, a hypothesis that was tested in the present study.
Specifically, subjects tried to reproduce from memory the tones of contemporary popular and rock songs that they had heard many times. I hypothesized that repeated exposure to a song creates a memory representation that preserves the actual pitches of the song, and that subjects would be able to access this representation in a production task. As it happens, Ward (1990) performed a similar study informally, by keeping a taped diary for several months of his spontaneous productions of songs that just popped into his head. He noticed that the keys employed tended to be within a semitone or two of the key in which the song was originally written. This question about the stability and absolute nature of pitch representations for popular songs has also been posed by Dennett (1991).
Contemporary popular and rock songs form an ideal stimulus for such a study, because they are typically encountered in only one version by a musical artist or group, and so the song is always heard - perhaps even hundreds of times - in the same key. In contrast, songs such as "Happy Birthday" and "Yankee Doodle" are performed in many different keys, and thus there is no objective standard for a single performance key. A recent study of auditory imagery used such folk songs to demonstrate the stability of mental representations. Halpern (1989) asked subjects on two different occasions to produce, recognize, or rate the opening tones of holiday and children's songs. She found that subjects tended to sing or select tones within two semitones of the same key from one occasion to the other. The stability she observed suggests that memory for pitch is stable over time. Yet, to address questions about the accuracy of pitch memory in an absolute sense, it is necessary to use songs that have an objective standard.
The absolute pitch issues discussed here are directly related to the issues of absolute representation addressed by the animal learning investigators. In this context, the study of musical memory offers a useful paradigm for exploring the extent of absolute and relational memory in humans. Whereas the identity of a song is determined by its melody (the relation of successive pitches), the auditory system initially processes actual musical pitches (the absolute perceptual information). It has previously been shown that humans do process the abstract relational information - most people have no trouble recognizing songs in transposition (Attneave & Olson, 1971; Deutsch, 1972, 1978; Dowling, 1978, 1982; Dowling & Bartlett, 1981; Idson & Massaro, 1978; Kallman & Massaro, 1979; Pierce, 1983). What remains to be demonstrated is whether people retain the original pitch information; more generally, what Bower (1967) calls the primary code. If people do maintain both kinds of information in memory, this would suggest that a dual representation exists in memory for melody: coding of the actual pitches as well as coding of the system of intervallic relations between tones.
Method
Subjects. The subjects were 46 Stanford University undergraduate and graduate students, and all served without pay. The undergraduates served to fulfill a course requirement for Introductory Psychology. The subjects did not know in advance that they were participating in a study involving music, and the sample included subjects with and without some musical background. The subjects ranged in age from 16 to 35 years (mean 19.5; mode 18; std. dev. 3.7). Two subject claimed to possess AP, although this claim was not tested.
Materials. Prior to the experiment, a norming study was conducted to select the stimuli; 250 introductory-psychology students completed a questionnaire about their familiarity with 50 popular songs. These subjects were also given the opportunity to provide the names of songs they "knew well and could hear playing in their heads." None of the subjects in the norming study were subsequently used in the main experiment.
The results of this norming study were used to select the best known songs. Songs on this list that had been performed by more than one group were excluded from the stimulus set because of the possibility that these versions might be in conflicting keys, creating interference with subjects' memories. (Examples of such songs include The Beatles' "Yesterday" and Stevie Wonder's "You Are the Sunshine of My Life.") In addition, songs in which tight vocal harmonies render the main melody hard to discern were excluded. (Examples include The Everly Brothers "Dream," Jane's Addictionís ìBeen Caught Stealingî and many songs by the group Wilson Phillips.) The 58 Compact Discs (CDs) containing the best known songs were included in this study and since most CDs contain at least 10 songs, over 600 songs were available to the subjects. These songs included "Hotel California" by The Eagles, "Like A Prayer" by Madonna, "Every Breath You Take" by The Police, and "When Doves Cry" by Prince. (The complete list of stimulus CDs and song titles chosen is available from the author.)
Procedure. Upon arriving at the experiment, each subject filled out a questionnaire to gather background information about gender, age, and musical training. After completing the questionnaire, the subjects were seated in a sound attenuation booth with the experimenter. The 58 CDs chosen from the norming study were displayed alphabetically on a shelf in front of the subjects. The experimenter followed a written protocol asking subjects to select from the shelf, and to hold in their hands, a CD that contained a song they knew very well. Holding the CD and looking at it may have provided a visual cue for subsequent auditory imaging.
The subjects were then asked to close their eyes, and to imagine that
the song was actually playing in their heads. They were instructed to try
to reproduce the tones of that song by singing, humming, or whistling,
and they were told they could start anywhere in the tune that they liked.
Subjects' productions were recorded on digital audio tape (DAT), which
accurately preserved the pitches they sang (digital recording avoids the
potential pitch and speed fluctuations of analog recording). The subjects
were not told how much of the song they should sing, but they typically
sang a four-bar phrase, yielding 12 to 20 tones. Following this first production,
subjects were asked to choose another song and repeat the procedure. Three
of the subjects discontinued participation after Trial 1.
The subjects' productions were later compared to the actual tones sung
by the artists on the CDs. Errors were measured in semitone deviations
from the correct pitch. The first three tones the subjects sang were coded
and compared to the equivalent three tones on the CD. For the main analysis,
octave errors were not penalized, on the assumption that subjects with
pitch memory would have a stronger representation for pitch class than
pitch height. This is consistent with modern practice in absolute pitch
research (Ward & Burns, 1982; Miyazaki, 1988, 1990; Takeuchi &
Hulse, 1993). For example, Miyazaki (1988) stated that octave errors are
actually characteristic of AP possessors; Deutsch (1969) proposed a neural
model of the brain that might represent octave equivalent pitch categories.
(For a related discussion, see Bachem, 1954; Bharucha, 1992; Rakowski &
Morawska-Büngeler, 1987). To obtain octave normalized data, an octave
was added or subtracted as necessary from some of the tones produced so
that all tones fell within one-half octave (six semitones) on either side
of a given target tone. Thus, if a subject sang D3 to a target of C4, this
was coded in the main analysis as a deviation of +2 semitones, not a deviation
of -10 semitones.
Analysis. The subjects were recorded monophonically on a Sony TCD-D3 DAT recorder at either 44.1Khz or 48Khz sampling rate, with Ampex R-467 C60 tape, through either AKG SDE-1000 or Akai ACM-100 electret condenser microphones, hidden from the subjects' view. The microphone was run through a Yamaha RM200 mixer for amplification. The subjects' productions were transferred digitally to a NeXT computer via the Singular Solutions AD64/X interface, and the sample rate was converted to 22.05 KHz. Subject data never left the digital domain.
Data coding of the subject productions was carried out using Spectro, a Fast Fourier Transform (FFT) application for the NeXT machine written by Perry Cook (Cook, 1992). Spectro computed the pitch of the fundamental frequency for each tone; this was converted to pitch class and octave by means of a lookup table. Measurement of the subjects' pitch was accurate to within 3 cents, and these measurements were then quantized to the nearest semitone.
In tone production on any instrument with continuously variable pitch - such as voice, woodwind, and brass instruments - each tone begins with an attack transient and ends with a decay transient. These transients contain sounds that are not part of the performer's tonal concept; the tone is closest to the performer's concept during its steady state portion, and it is during this portion that listeners' pitch judgments are made (Campbell & Heller, 1979). Accordingly, gross fluctuations at the beginning and end of a given tone (<100 ms) were considered to be transitions, and were edited out using a waveform editing program, SoundEdit, on the NeXT. The resulting tonal sample was analyzed with Spectro. Of course, even these remaining samples were rarely actual steady state tones, but contained vibrato and slight tonal fluctuations either intentional or unintentional on the part of the singer. Because the perceived pitch of a vibrato tone is the mean of the frequencies (Shonle & Horan, 1990; Sundberg, 1987), the analysis technique used provided accurate pitch information.
The CD melodies were coded using a Magnavox CD114 CD player run through a Yamaha CR600 stereo receiver. The "tape out" of the receiver fed a Seiko ST-1000 digital tuner and a Conn Strobotuner in series. The tuners' accuracy was verified using Spectro; the Seiko was accurate to within 0.01% and the Conn to within 0.1%. Although the vocal lines were not entirely isolated from the background music, this coding scheme proved effective. The vocal lines usually activated the tuner, and as a double check, the data coder used a Yamaha DX7 digital synthesizer to match the performance key and verify chroma and octave. Measurements using this coding scheme were accurate to within a semitone.
A trained vocal musician independently analyzed 11 randomly selected songs and the corresponding subject productions and these analyses were in complete agreement with those obtained by the data coder.
Results
The first three tones produced by the subjects were compared to the equivalent three-tone sequence on the CDs. The average errors across the three-tone sequence did not differ significantly from the errors using each of the three tones individually, and a repeated-measures ANOVA for the three tones revealed no significant effect of tone position (F (90,2) = .58, p=.56). Therefore, the analyses are based on subjects' first-tone productions.
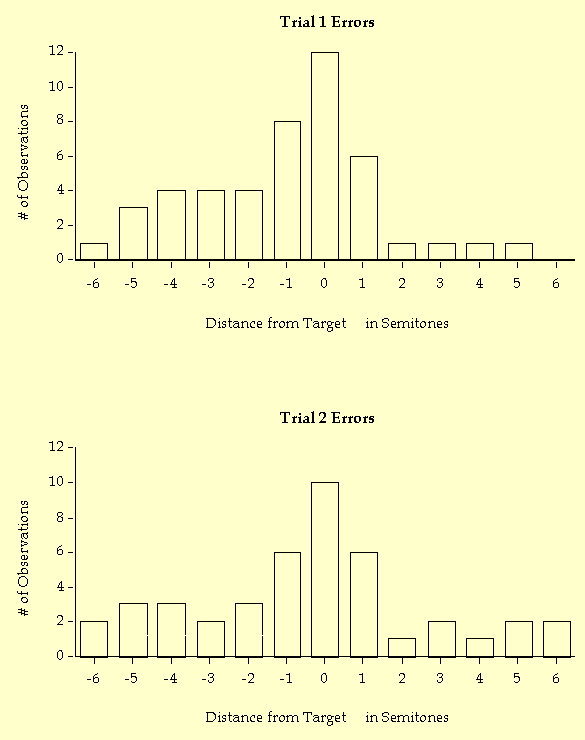
Figure 1 displays subject errors in semitone deviations from the correct pitch for Trials 1 and 2. As described in the previous section, octave errors were adjusted to fall within one half octave on either side of the correct pitch. (Note that a deviation of -6 semitones yields the same pitch class as a deviation of +6 semitones. Both were included for the sake of symmetry in the accompanying figures, and subject errors of ±6 were distributed evenly between the two extreme categories.) The most reasonable null hypothesis is that people can't remember actual pitches at all; if that were true, we would expect a rectangular distribution of errors and each error category to contain 1/12 of the responses, or 8.3%. But, as Figure 1 illustrates, the errors approximate a normal curve. A Rayleigh test was peformed, and the hypothesis of uniformity was rejected in favor of a hypothesis that the data fit a circular normal (von Mises) distribution. For Trial 1, r=.48, p<.001; for Trial 2, r=.30, p<.02. Because the underlying metric for octave normalized pitch is circular, not linear (Krumhansl, 1990; Shepard, 1964), a circular statistic such as the Rayleigh test was required rather than the more common linear goodness-of-fit tests (Batschelet, 1981; Fisher, 1993; Levitin, 1994).
On Trial 1, 12 of the 46 subjects (26%) made no errors; 26 subjects (57%) were within one semitone and 31 subjects (67%) were within two semitones of the correct pitch. On Trial 2 there were 43 subjects and 10 of these (23%) made no errors; 22 subjects (51%) were within one semitone and 26 (60%) were within two semitones of the correct pitch. One of the subjects who claimed to possess AP made an error of -1 semitone on Trial1 (this subject was one of the three who, for various reasons, discontinued the experiment before completing Trial 2). The remaining subject who claimed to possess AP made errors of +1 and -2 semitones on Trials 1 and 2 respectively.

Figure 1. Subjects' errors in semitone deviations from the correct tone. Octave errors were not penalized. Both curves are normal by Kolmogorov-Smirnov test. (a) Trial 1. Mean = -0.98, s = 2.36. (b) Trial 2. Mean = -0.4, s = 3.05.
To measure consistency across trials, trials on which the subjects made no error were considered "hits" and all others were considered "misses." Table 1 shows a 2x2 contingency table of hits and misses for the 43 subjects who completed both trials. Yule's Q was computed as a measure of strength of association and was found to be .58, p=.01.1 Further inspection of Table 1 reveals that 5 subjects (12%) hit the correct tone on both trials, and 17 subjects (40%) hit the correct tone on at least one trial. Broadening the definition of a hit, 19 subjects (44%) came within 2 semitones of the correct pitch on both trials, and 35 subjects (81%) came within 2 semitones on at least one trial.
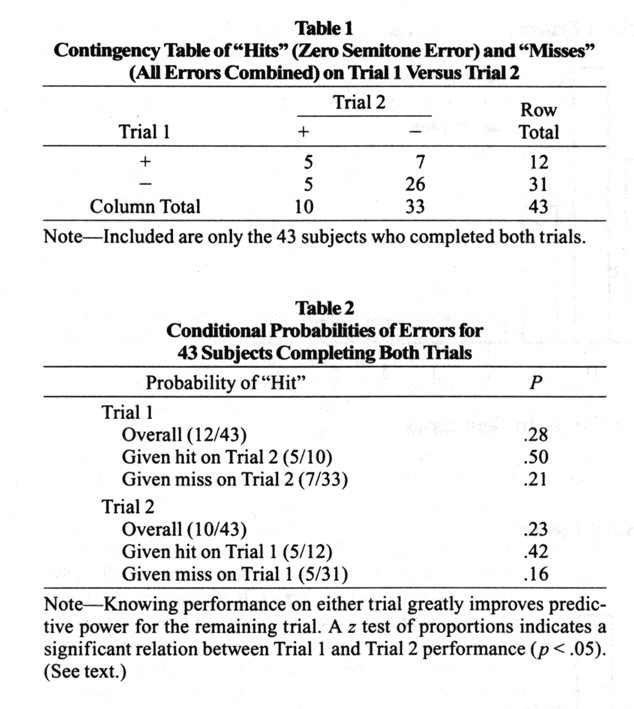
An analysis of conditional probabilities makes the degree of association between the trials still clearer. If there were no association between the two trials, the probability of a hit on Trial 2 should be the same whether the subject obtained a hit or a miss on Trial 1. As Table 2 reveals, this was not the case: P(Hit Trial 2 | Hit Trial 1) = .42, and P(Hit Trial 2 | Miss Trial 1) = .16. A z-test for proportions was performed, and was found to be significant, Z=1.66, p<.05. For prediction in the reverse direction, P(Hit Trial 1 | Hit Trial 2) = .50, and P(Hit Trial 1 | Miss Trial 2) = .79; Z = 1.67, p< .05. Another way to consider this relation is that the overall probability of a hit on Trial 2 was .28, but the conditional probability of a hit on Trial 2 given a hit on Trial 1 was .42; thus, knowing how a subject performed on Trial 1 provides a great deal more predictive power for Trial 2 performance. Looking at this in the opposite direction, the overall probability of a hit on Trial 2 was .28, and the conditional probability of a hit on Trial 2 given a hit on Trial 1 was .50. In summary, it was far more likely that a subject who obtained a hit or a miss on one trial performed equivalently on the other. That is, 31 subjects (72%) were consistent in their performance across trials.
A correlational analysis was used to test whether any of the items on the background questionnaire were related to success at this task. No reliable relation was found between performance and gender, handedness, age, musical training, amount of time spent listening to music, or amount of time singing out loud (including in the shower or car).
Figure 2 displays the same error data without the octave adjustments. Productions that deviated more than one-half octave (six semitones) in either direction from their target pitch can be considered octave errors. 12 subjects made such octave errors on each of Trial 1 and Trial 2. Of course, some octave errors are to be expected, for example, when subjects are trying to match pitch with a singer of the opposite gender. In addition, popular music taste has tended for the last twenty years or so to prefer those singers - both male and female - with voices higher than average. Paula Abdul, Madonna, Sting and Robert Plant are examples of popular singers with voices higher than average in pitch. For Trial 1, half of the octave errors were attributable to subjects singing across gender (two males attempting to sing female vocals and four females attempting to sing male vocals). The remaining octave errors were all from subjects attempting to match unusually high singing voices (one male, for example, trying to match Prince, and another trying to match Michael Jackson). Trial 2 octave errors followed a similar pattern.
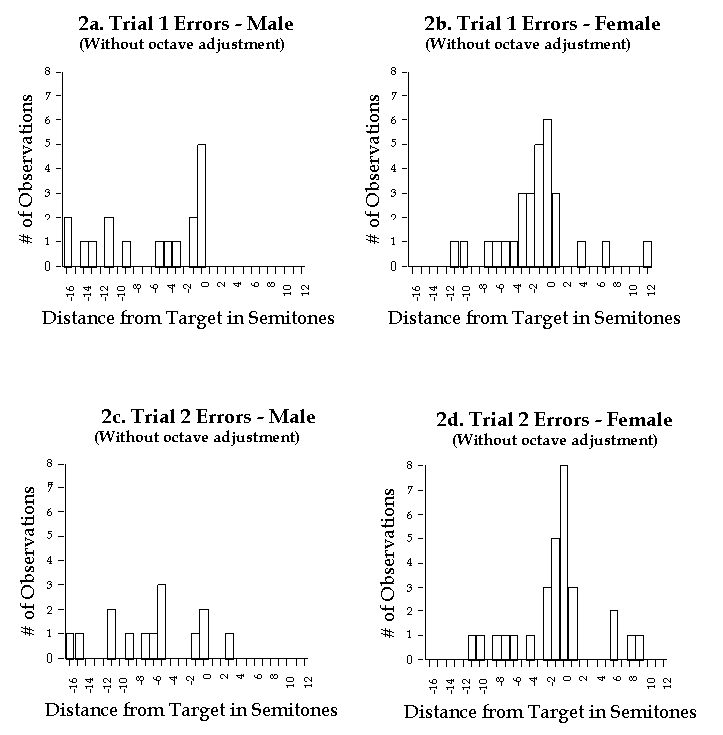
Figure 2. Subjects' actual errors in semitone deviations from the correct
tone, without octave adjustment.
One of the implicit assumptions in the preceding analyses is that the starting tones of the songs that subjects sang, and the tones they actually sang, are both uniformly distributed. One can easily imagine a world where all pop songs start on one or two tones, and where subjects who performed well in this task are those who managed to form a mental representation of that one tone. Recall however that subjects did not necessarily begin singing the first tone of their chosen song - they were allowed to start anywhere in the song they liked. So even if pop songs tend toward a limited set of musical keys (which is a defensible notion) the distribution of starting tones should still be uniform.
Figure 3 shows the distribution of the actual starting tones the subjects were attempting to sing, as well as the starting tones they did sing. The distributions do indeed appear more or less random and the results of Rayleigh tests show a satisfactory fit with a uniform distribution. For Figure 3a: r=.09, p>.69; 3b: r= .21, p>.15; 3c: r= .13, p>.47; 3d: r= .24, p>.09. Note, however, some interesting features of the distributions: no subject sang the tone "F" on either trial, and "C" was the modal choice of subjects for both trials. Although these failed to be statistically significant, the power of the tests is low due to the relatively small sample size.
As a control, one might ask what a distribution of starting tones would look like if random subjects were just asked to sing the first tone that comes to mind, without reference to any particular mental representation. Such a study was performed by Stern (1993), who found that subject productions under these circumstances were uniform. Interestingly, in her sample of 37, no one sang "G" and the modal response was "B." Yet, in both the present study and Stern's, these outcomes are explainable as chance fluctuations.
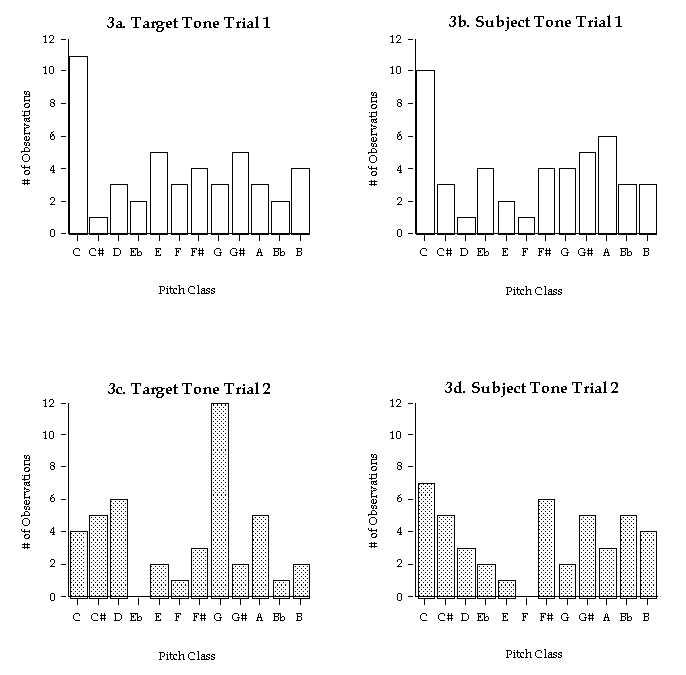
Figure 3. Distribution of starting tones for songs in this study. (a)
Actual starting tones ("targets") in songs selected in Trial
1. (b) Subjects' starting tones in songs selected in Trial 1. (c) Actual
tones in songs selected in Trial 2. (d) Subjects' tones in songs selected
in Trial 2. All distributions are uniform by Rayleigh test.
Similarly, one might wonder about the distribution of subject errors as a function of pitch class. These are displayed in Figure 4 (for Trial 1), and also appear random. Correlations between subjectsí tones and error, and actual tones and error, for both trials were found to be non-significant. (Trial 1: subject tone * error, r=.15, p>.35; actual tone * error, r=.26, p>.10. Trial 2: subject tone * error, r=.11, p>.47; actual tone * error, r=.10, p>.54.)

Figure 4. Distribution of errors as a function of pitch class for Trial
1. (a) Errors vs. the actual pitch of the tone (the subjects' "target"
tone). (b) Errors vs. subjects' tone. All points inside a given box represent
the same tone. Errors are randomly distributed among tones.
Discussion
The finding that one out of four subjects reproduced pitches without error on any given trial, and that 40% perform without error on at least one trial, provides evidence that some degree of absolute memory representation exists in the general population. To perform accurately on this task, subjects needed to encode pitch information for the songs they have learned, store the information, and recall it without shifting those pitches. Their memory for pitch can thus be characterized as a stable, long-term memory representation.
The distribution of errors made by subjects who ìmissedî is also instructive, and shows a convergence with the results of earlier investigators who used a recognition measure (Lockhead & Byrd, 1981; Terhardt & Ward, 1982; Terhardt & Seewan, 1983; Miyazaki, 1988). If those subjects who made errors had no absolute memory, we would expect their errors to be evenly distributed at all distances from the correct tone. Yet, on a given trial, over half of the subjects came within one semitone, and over 60% came within two semitones. This suggests that those subjects who made only slight errors might also have good pitch memory, but that it failed to show up in this testing procedure due to other factors, such as:
(a) a pitch memory with only a semitone resolution. Miyazaki (1988) has argued that this level of resolution should still qualify one as a possessor of absolute pitch; it seems reasonable to extend this to a definition of pitch memory. Indeed, Terhardt and Ward (1982) noted that "semitone discrimination turns out to be quite difficult, even for AP possessors" (p. 33). (For a further discussion of this issue, see also Lockhead & Byrd, 1981; Rakowski and Morawska-Büngeler, 198; Terhardt & Seewan, 1983.)
(b) production problems, in which the subjects were unable to get their voices to match the sounds they heard in their heads. Referring to AP possessors, Takeuchi and Hulse (1993) pointed out the asymmetry that not all people who can identify the pitch of a tone can also produce a tone at a given pitch. Thus, not everyone with absolute pitch also possesses absolute production, at least with respect to vocalizing.
(c) self-correction or self-monitoring deficits, in which the subjects either knew they were singing the wrong tone but could not correct it, or didnít know they were singing the wrong tone because of an inability to compare their own productions with their internal representations.
(d) exposure to the songs in keys other than the correct keys. This could have happened if subjects listened to, and learned, the songs on cassette machines or phonographs with inaccurate speeds. Cassette players and phonographs may vary as much as 5% in their speed (approximately one semitone) whereas CD players do not vary in pitch. To address this, subjects were asked where they had heard the songs before. A correlational analysis, however, showed no relation between accurate performance and the source of learning the songs.
Examination of Figures 1 and 2 reveals that most of the errors fall to the left of center; that is, subjects tended to sing flat when making errors. (This is revealed in Figure 4a as well, with most errors falling below the zero center line.) The explanation of this is uncertain. It may be merely the so-called "lounge singer effect" widely noted by vocal instructors, wherein amateur singers tend to undershoot tones and to sing flat. Alternatively, it may be a range effect such that subjects found themselves attempting to sing songs that were above their range.
Whereas the present results suggest that absolute pitch information is stored by many subjects, pitch is undoubtedly only one of many features contained in the original stimulus that is stored in memory. It seems likely that one's internal representation of the song contains many components, such as timbre, tempo, lyrics and instrumentation; indeed, the entire spectro-temporal pattern of the song may well be represented. The subjects reported that they had no trouble imagining the songs, and heard them as if they were actually playing in their heads. This quality of auditory imagery has been previously noted by Halpern (1988). Thus, pitch might be only one and not necessarily the most important of the stored components. In particular, timbral cues contained in the memory representation might assist people in retrieving the proper pitch; the present study wasn't able to distinguish whether pitch was accessed directly by the subjects or derived from other features.
The concordance measures for between Trial 1 and Trial 2 are reasonably high, but still, many people did not perform consistently. One explanation for this could be that people have an absolute representation for some songs and not others. Alternatively, the process of singing the first song may have established a tonal center for some subjects, biasing subsequent productions. That is, information about the melody of a song may be represented more strongly in memory than information about its actual pitches. Some subjects may have had difficulty ignoring the tonal center established by the first song and they consequently started the second song on a different pitch than they otherwise would have. Tsuzaki (1992) reported that the internal standard for AP possessors is subject to interference; it seems possible that the reference frame for pitch memory possessors could also be influenced by a preceding tonal context.
How do the mental representations of the pitch memory possessors in this study differ from those of traditional AP possessors? AP possessors probably associate a label with each pitch at the time of encoding (Zatorre & Beckett, 1989), and this label becomes another component of the representation. It is probably not the case that AP possessors store the labels without also storing the sensory information; this would be inconsistent with reports that AP possessors often feel uncomfortable hearing a well-known piece performed out of key (Miyazaki, 1993; Ward & Burns, 1982).
It has been suggested that subjects in this task merely relied on muscle memory from their vocal chords to find the correct pitches. There is always some degree of muscle memory involved in the vocal generation of pitch (Ward & Burns, 1978, Cook, 1991). The initial pitch of a vocal tone is, by necessity, determined by muscle memory; only on long tones does one have time to correct a wrong tone using auditory feedback. Zatorre and Beckett (1989) argued that true AP possessors do rely on muscle memory to some extent, and this is not interpreted as diminishing their abilities (c.f. Corliss, 1973). Nevertheless, studies have shown that muscle memory for pitch is not very accurate. Ward and Burns (1978) denied auditory feedback to trained singers (forcing them to rely solely on muscle memory); the singers erred by as much as a minor third, or three semitones. Murry (1990) examined the first five waveforms of vocal productions (before auditory feedback could take effect) and found that subjects who were otherwise good at pitch-matching made average errors of 2-1/2 semitones, and errors as large as 7-1/2 semitones. Therefore, the present experiment seems to have tested, as well as possible, subjects' memory for particular auditory stimuli.
Conclusions
The present study provides evidence that, for at least some well-known popular songs, a larger percentage of people than previously recognized possess absolute memory for musical pitch. 12% of the subjects performed without error on both trials, and 40% performed accurately on at least one trial. These subjects were able to maintain stable and accurate representations of auditory memories over a long period of time with much intervening distraction. The ability seems independent of a subject's musical background, or other factors such as age or gender. The concordance across trials was significant, with 72% performing consistently. Using a broader definition of success reveals that 44% of the subjects came within two semitones on both trials, and 81% came within two semitones on at least one trial.
The findings also provide evidence for the two-component theory of Absolute Pitch. Although the present subjects presumably do not have the ability to label pitches (because all but two claimed they did not possess AP), they did exhibit the ability called pitch memory, demonstrating that this ability is independent of pitch labeling. The puzzle of why AP, as traditionally defined, exists in such small numbers, and why previous studies have hinted at the existence of "latent absolute pitch abilities," may now become more tractable. It might be the case that many people possess pitch memory, but never acquired pitch labeling, possibly because they lacked musical training or exposure during a critical period.
Over fifty years ago, the Gestalt psychologists proposed that memory is the residue of the brain process underlying perception. In a similar vein, Massaro (1972) argued that ìan auditory input produces a preperceptual auditory image that contains the information in the auditory stimulus. The image persists beyond the stimulus presentation and preserves its acoustic informationî (p. 132). The present finding of absolute memory for pitch supports this view.
Taken together, the present study and previous findings suggest that the people are capable of retaining both abstract relational information (in this case, melody) as well as some of the absolute information contained in the original physical stimulus, and further, that these representations are separable. One should be cautious, however, about jumping to conclusions. Subjects who exhibit pitch memory are not necessarily exhibiting perceptual memory (as in the perceptual residue the Gestalt psychologists spoke of), but it is clear that their memories are to some extent veridical, and that they retain access to some absolute features of the original stimulus. We might now ask to what extent - and in what other sensory domains - this type of dual representation exists.
References
Attneave, F., & Olson, R.K. (1971). Pitch as a medium: A new approach to psychophysical scaling. American Journal of Psychology, 84, 147-166.
Bachem, A. (1954). Time factors in relative and absolute pitch determination. Journal of the Acoustical Society of America, 26, 751-753.
Baggaley, J. (1974). Measurement of Absolute Pitch. Psychology of music, 2(2), 11-17.
Batschelet, E. (1981). Circular statistics for biology. London: Academic Press.
Bharucha, J.J. (1992). Tonality and learnability. In M. R. Jones & S. Holleran (Eds.), Cognitive bases of musical communication. Washington, D.C.: American Psychological Association.
Bishop, Y.M.M.; Fienberg, S.E.; & Holland, P.W. (1975). Discrete multivariate analysis: Theory and Practice. Cambridge, MA: MIT Press.
Bower, G.H. (1967). A multicomponent theory of the memory trace. In K. W. Spence and J. T. Spence (Eds.), The psychology of learning and motivation: Advances in research and theory (Vol. 1). New York: Academic Press.
Campbell, W.C., & Heller, J. (1979). Convergence procedures for investigating music listening tasks. Bulletin of the Council for Research in Music Education, 59, 18-23.
Cook, P. R. (1991). Identification of control parameters in an articulator vocal tract model, with applications to the synthesis of singing. Dissertation Abstracts International, B52, 419. (Univ. microfilms #9115756.)
Cook, P. R. (1992). Spectro. Freeware [available by anonymous ftp from ccrma.stanford.edu]. Stanford University.
Corliss, E.L. (1973). Remark on ìfixed-scale mechanism of absolute pitch.î Journal of the Acoustical Society of America, 53(6), 1737-1739.
Dennett, D. C. (1991). Consciousness explained. Boston: Little, Brown and Company.
Deutsch, D. (1969). Music recognition. Psychological Review, 76, 300-307.
Deutsch, D. (1972). Octave generalization and tune recognition. Perception and Psychophysics, 11, 411-412.
Deutsch, D. (1978). Octave generalization and melody identification. Perception and Psychophysics, 23, 91-92.
Deutsch, D. (1991). The tritone paradox: An influence of language on music perception. Music Perception, 8(4), 335-347.
Deutsch, D. (1992). The tritone paradox: Implications for the representation and communication of pitch structure. In M. R. Jones & S. Holleran (Eds.), Cognitive bases of musical communication. Washington, D.C.: American Psychological Association.
Deutsch, D., Kuyper, W.L., & Fisher, Y. (1987). The tritone paradox: Its presence and form of distribution in a general population. Music Perception, 5(1), 79-92.
Deutsch, D., Moore, F.R., & Dolson, M. (1986). The perceived height of octave-related complexes. Journal of the Acoustical Society of America, 80(5), 1346-1353.
Dowling, W. J. (1978). Scale and contour: Two components of a theory of memory for melodies. Psychological Review, 85(4), 341-354.
Dowling, W. J. (1982). Melodic information processing and its development. In D. Deutsch (Ed.), The psychology of music. New York: Academic Press.
Dowling, W. J., & Bartlett, J.C. (1981). The importance of interval information in long-term memory for melodies. Psychomusicology, 1, 30-49.
Fisher, N.I. (1993). Statistical analysis of circular data. Cambridge: Cambridge University Press.
Halpern, A.R. (1988). Mental scanning in auditory imagery for songs. Journal of Experimental Psychology: Learning, Memory and Cognition, 14(3), 434-443.
Halpern, A. R. (1989). Memory for the absolute pitch of familiar songs. Memory and Cognition, 17 (5), 572-581.
Handel, S. (1989). Listening: An introduction to the perception of auditory events. Cambridge: MIT Press.
Hanson, H.M. (1959). Effects of discrimination training on stimulus generalization. Journal of Experimental Pscyhology, 58, 321-334.
Hayman, C.A.G., & Tulving, E. (1989). Contingent dissociation between recognition and fragment completion: The method of triangulation. Journal of Experimental Psychology: Learning, Memory,l and Cognition, 15(2), 228-240.
Idson, W.L., & Massaro, D.W. (1978). A bidimensional model of pitch in the recognition of melodies. Perception and Psychophysics, 24(6), 551-565.
Kallman, H.J., & Massaro, D.W. (1979). Tone chroma is functional in melody recognition. Perception and Psychophysics, 26(1), 32-36.
Kohler, W. (1939). Simple structural function in the chimpanzee and the chicken. In W.D. Ellis (Ed.), A sourcebook of Gestalt psychology. New York: Humanities Press, 1950.
Kolb, B., & Whishaw, I.Q. (1990). Fundamentals of human neuropsychology. (3rd Ed.) New York: Freeman.
Krumhansl, C. L. (1990). Cognitive foundations of musical pitch. New York: Oxford University Press.
Levitin, D.J. (1994). Limitations of the Kolmogorov-Smirnov Test: The need for circular statistics in Psychology. Manuscript submitted for publication.
Lockhead, G. R., & Byrd, R. (1981). Practically perfect pitch. Journal of the Acoustical Society of America, 70(2) 387-389.
Luria, A.R. (1968). The mind of a mnemonist. New York: Basic Books.
Massaro, D. W. (1972). Perceptual images, processing time, and perceptual units in auditory perception. Psychological Review, 79(2), 124-145.
Miyazaki, K. (1988). Musical pitch identification by absolute pitch possessors. Perception and Psychophysics., 44 (6), 501-512.
Miyazaki, K. (1990). The speed of musical pitch identification by absolute pitch possessors. Music Perception, 8(2), 177-188.
Miyazaki, K. (1993). Absolute pitch as an inability: Identification of musical intervals in a tonal context. Music Perception. 11(1), 55-72.
Murry, T. (1990). Pitch-matching accuracy in singers and non-singers. Journal of Voice. 4(4), 317-321.
Nelson, T.O. (1984). A comparison of current measures of the accuracy of feeling-of-knowing predictions. Psychological Bulletin, 95(1), 109-133.
Pierce, J.R. (1983). The science of musical sound. New York: Scientific American Books/Freeman.
Profita, J., & Bidder, T.G. (1988). Perfect pitch. American Journal of Medical Genetics, 29, 763-771.
Rakowski, A., & Morawska-Büngeler, M. (1987). In search of the criteria for absolute pitch. Archives of Acoustics, 12(2), 75-87.
Reese, H.W. (1968). The Perception of sitmulus relations. New York: Academic Press.
Shepard, R.N. (1964). Circularity in judgments of relative pitch. Journal of the Acoustical Society of America, 36(12), 2346-2353.
Shonle, J., & Horan, K. (1980). The pitch of vibrato tones. Journal of the Acoustical Society of America, 67, 246-252.
Spence, K.W. (1937). The differential response in animals to stimuli varying within a single dimension. Psychological Review, 44, 430-444.
Stern, A.W. (1993). Natural pitch and the A440 scale. Unpublished manuscript, Stanford University, Center for Computer Research in Music and Acoustics, Stanford, CA.
Stromeyer, C.F. III. (1970). Eidetikers. Psychology Today, (November), 76-80.
Sundberg, J. (1987). The Science of the singing voice. Dekalb, Il: Northern Illinois University Press.
Takeuchi, A.H., & Hulse, S.H. (1993). Absolute pitch. Psychological Bulletin, 113(2), 345-361.
Terhardt, E., & Seewan, M. (1983). Aural key identification and its relationship to absolute pitch. Music Perception, 1, 63-83.
Terhardt, E., & Ward, W. D. (1982). Recognition of musical key: Exploratory study. Journal of the Acoustical Society of America, 72 (1), 26-33.
Tsuzaki, M. (1992). Interference of preceding scales on absolute pitch judgment. Paper presented at the 2nd International Conference on Music Perception and Cognition, Los Angeles, CA, February 23, 1992.
Ward, W.D. (1990). Paper presented at von Karajan Symposium, Vienna.
Ward, W. D. & Burns, E. M. (1978) . Singing without auditory feedback. Journal of Research in Singing and Applied Vocal Pedagogy, 1(2), 24-44
Ward, W. D., & Burns, E. M. (1982). Absolute pitch. In D. Deutsch (Ed.), The psychology of music. New York: Academic Press.
Zatorre, R. J., & Beckett, C. (1989). Multiple coding strategies in the retention of musical tones by possessors of absolute pitch. Memory & Cognition, 17(5), 582-589.
Author Note
This research was supported by NSF Research Grant BNS 85-11685 to Roger N. Shepard, by ONR Grant N-00014-89-J-3186 to the author, while the author held a National Defense Science and Engineering Graduate Fellowship, and by ONR Grant N-00014-89-3013 to Michael I. Posner. The Center for Computer Research in Music and Acoustics at Stanford (CCRMA) and the Department of Music at the University of Oregon generously provided essential equipment for the study.
I am greatly indebted to Roger Shepard and Perry Cook for their valuable assistance throughout every phase of this project. I am also indebted to the following for their many helpful insights: Gordon Bower, Anne Fernald, Lew Goldberg, Ervin Hafter, Doug Hintzman, Jay Kadis, Carol Krumhansl, Gerald McRoberts, John Pierce, John Pinto, Mike Posner, Peter Todd, and Robert Zatorre; and to Clarence McCormick, Paul Slovic and Marjorie Taylor for their statistical help.
Preliminary versions of this work were presented at the annual meetings of the Audio Engineering Society, San Francisco, CA (1992); Western Psychological Association, Phoenix, AZ (1993); and the Society for Music Perception and Cognition, Philadephia, PA, (1993).
As of 8/1/96, address correspondence to: Daniel Levitin,
Behavioral Science Laboratory, Interval Research Corporation , 1801C Page
Mill Road, Palo Alto, CA 9430. Phone: (650) 842-6236. E-mail: levitin@interval.com
FOOTNOTE
1. For a 2x2 contingency table, Yule's Q is the same as Goodman & Kruskal's Gamma. If the joint event of a hit on each trial is represented in cell a, and the joint event of a miss on each trial is represented in cell d, with "hit-miss" and "miss-hit" represented in cells b and c, the formula for Q is:
Q (= G) = ad-bc/ad+bc.
For further discussion on the use of Q and G as association
measures, see Bishop, Fienberg & Holland, 1975; Hayman & Tulving,
1989; Nelson, 1984.