A connectionist model for categorical perception and symbol grounding
Alberto Greco
Department of Anthropological and Psychological Sciences, University of Genoa (I)
Angelo Cangelosi *
Centre for Neural and Adaptive Systems, University of Plymouth (UK)
Stevan Harnad
Cognitive Science Centre, University of Southampton (UK)
Abstract
Neural network models of categorical perception can help solve the symbol-grounding problem [5,6] by connecting analog sensory projections to symbolic representations through learned category-invariance detectors in a hybrid symbolic/nonsymbolic system. Our nets learn to categorize and name geometric shapes. The nets first learn to do prototype matching and then entry-level naming, grounding the shape names directly in the input patterns via hidden-unit representations. Next, a higher-level categorization is learned indirectly from combinations of the grounded category names (symbols). We analyze the architectures and input conditions that allow grounding to be "transferred" from directly grounded entry-level category names to higher-order category names.
How do symbols mean something? One candidate answer is "by definition," but a definition just consists of further symbols: Where do they get their meaning? This is the symbol grounding problem [5]. To embody thought, a cognitive system must be autonomous: the connections between its symbols and what they stand for must be direct and intrinsic to the system rather than mediated by an external user.
To identify an object, one must somehow detect the invariant features in its "iconic representations" (sensory traces), the features that make them icons of that particular object (or kind of object) rather than another; the rest of the features must be ignored. These categorical representations are still only sensory rather than symbolic, because they still preserve some of the "shape" of the sensory projections, but this shape has been "warped" in the service of categorization: The feature filtering has compressed within-category differences and expanded between-category distances in similarity space so as to allow a reliable category boundary to separate members from nonmembers. This compression/expansion effect is called "categorical perception" [4] and has been shown to occur with both human subjects [2] and neural nets [7] during the course of category learning.
One of the most natural capabilities of neural nets is category learning. Nets can be trained to detect the invariants in sensory input patterns that allow them to be sorted in a specified why. Once the patterns have been sorted, the category can be given a name. That name is then grounded in the system's autonomous capacity to pick out what the name refers to without the mediation of a user.
The training of both neural nets and people to categorize through trial and error with corrective feedback has come to be called "supervised learning," but we will refer to it here as the acquisition of categories through direct sensorimotor grounding (Sm) to contrast it with a radically different way of acquiring categories, which we will indirect symbolic grounding (Sy). The outcome of Sm is a new category and usually also a new name for it; the name can then serve as a grounded elementary symbol. Acquiring a category through Sy is based on symbols only, rather than on sensorimotor interaction: The category is described by a proposition composed of grounded symbols.
In the simulations described below, we test what happens when nets that first acquire a set of categories by Sm are then taught an H-Level category by Sy.
2. Method
2.1 The stimulus set
Our neural nets were trained to categorize and name 50 by 50 pixel images of circles, ellipses, squares and rectangles projected onto the receptive field of a 7 by 7 unit "retina." Once the net had grounded these four Entry-Level (E-Level) category names ("circle," "ellipse," etc.) through direct trial and error experience supervised by corrective feedback (Sm), it was taught the Higher-Level (H-Level) category "symmetric/asymmetric" on the basis of strings of symbols alone (Sy).
A total of 292 stimuli were used (256 training, 32 test, and 4 teaching input stimuli). The 256 stimuli consisted of four groups of circles, ellipses, squares, and rectangles. In each group there were 64 (8 by 8) stimuli that varied in size (8 sizes generated by reducing the diameter by two pixels) and retinal position (8 positions generated by shifting the center of the figure by 1 pixel in the eight adjacent cells). The 32 test stimuli were also subdivided into four groups of eight stimuli each, one for each size. Position for each size was hence fixed, but varied across sizes. The four teaching inputs were the largest instances of each shape.
2.2 Neural networks and learning tasks
Ten 3-layered feed-forward nets differing in their random initial weights were exposed to the 256 training stimuli during the three learning stages. The input layers consisted of two groups of units: the retina, with 49 units (7 by 7) and the 6 linguistic units (one each for the six category names: "circle" "ellipse" "square" "rectangle" "symmetric" and "asymmetric"). The hidden layer had five units receiving connections from both groups of input units. The output had the same organization as the 49 retinal units plus 6 symbolic-name units.
Whereas the coding of the symbolic units was localist, (i.e., each unit was on when its corresponding label was active), the coding of the retinal units was more complex. We used the coding system of [3] with retinal units receiving activation from their receptive fields in the 50 by 50 pixel matrix depicting each of the 256 geometric figures. The receptive field of one retinal unit was a circular area 11 (partially overlapping) pixels in diameter. Because of the receptive field overlap (3 pixels), there were 49 receptive fields arranged in 7 columns by 7 rows. The activation formula for the retinal units used the Gaussian distribution centered on the receptive field. Hence pixels in the center of the field contributed more to the activation of the retinal unit than those in the periphery.

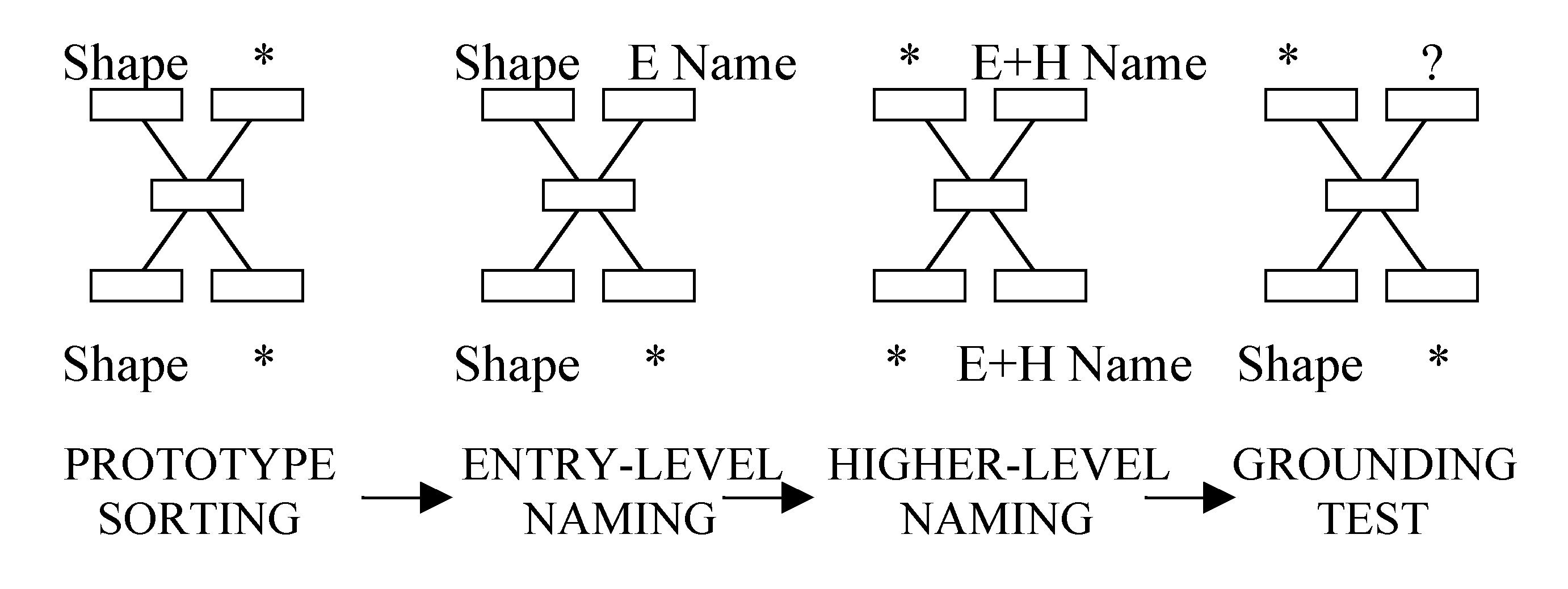
The training procedure consisted of three stages for category learning and naming: (1) prototype-based sorting, (2) E-Level naming, and (3) H-Level naming (figure 1). In all the learning stages in which names were used there was a further imitation task.
Figure 1: Neural network architecture showing the input and output in the learning and test stages. The absence of input or output in the specified set of units is indicated by *.
Prototype-Based Sorting
. The net was first trained, via backpropagation, to sort the 256 training stimuli into the four categories (64 stimuli each) by producing as output the "prototype" of each category in the form of the largest circle, ellipse, square or rectangle (coded the same way as the rest of the stimuli).Entry-Level Naming. The net next learned to respond to each stimulus by producing both its prototype shape and its category name.
Higher-Level Naming. H-Level categories such as "symmetric/ asymmetric" can be learned in one of two ways, either (1) directly from the retinal input, as with the E-Level categories (Sm), or (2) from combinations of the grounded category names (Sy). We investigated (2): The net received as input the combination of the grounded name plus a new name ("asymmetric" or "symmetric") and was required, through error-correcting feedback, to generate both names as output. (Simultaneous presentation of e-level and h-level names makes it unnecessary to use a recurrent network to learn the association.) A net that learns that two different grounded names, "circle" and "square," are always combined with the same new name, "symmetric," should be able to name a circle both "circle" on the basis of the prior (Sm) grounding, and "symmetric" on the basis of the new symbolic grounding (Sy).
Imitation learning. The imitation task is alternated with each trial of the naming task. It consists of an extra spreading cycle that allows the net to "practice" on the category name that has been learned in the previous naming cycle.
Backpropagation. One learning epoch consists in the presentation of all 256 training stimuli. The first learning stage (Prototype-Based Categorization) consists of 10,000 epochs. This is necessary because of the large number of retinal units (49) that need to be trained. The other two learning stages require only 2,000 epochs. Each learning condition is replicated with 10 nets with different random weight initializations. The 10 replications of the second and third stages, however, are constrained to the weights that were trained in their previous phase.
3. Results
3.1 Learning and categorical perception effects
All ten nets learned the three tasks successfully. The pattern of error decreases in all three conditions is a rapid initial decrease in the early training epochs. After that, the error decreases very little. The results of the generalization test showed that after the prototype learning the 32 test stimuli were properly classified in the four E-Level categories.
At the level of the hidden units, the net builds categorical representations which must sort each icon reliably and correctly into its own category. This can be thought of as a feature-filter that reduces the category confusability by decreasing the within-category differences among the icons and increasing the between-category differences as needed to master the task [4].
For the three learning stages of each of the 10 nets, we computed means and variances in the Euclidean distances for all 256 representations in the 5-dimensional hidden unit activation space. We first computed the central (mean) points for the four categories. These were then used to compute both within- and between-category distances. The within-category variance is a measure of the distance between each of the 64 points and its respective category mean. There is a statistically significant decrease in within-category variance from before prototype learning (.315) to after (.2). That is, during the course of the prototype learning the 64 points of each category move closer to one another. A further within-category compression from prototype matching (.2) to naming (.172) shows the effects of arbitrary naming on categorical representations (prototypes are analog, names are arbitrary).
The same effects are observed with the between-category differences (the distances between the centers of the four categories). From before learning (.15) to prototype matching (1.14), the average between-category distance increases for all six pairwise comparisons between the four category means. A further but smaller increase occurs with naming.
3.2 Grounding transfer
We next tested whether grounding could be "transferred" from directly grounded names to H-Level ones. Can a net that has learned the category "symmetric" indirectly through Sy generalize it to the direct retinal input? To test this, after the H-Level learning we presented the retinal stimuli alone (see figure 1, last column) and computed the frequency of correct responses for the E-Level names (criterion for all conditions: correct bit > 0.5, others < 0.5)
Nine of the ten nets gave the correct Entry- Level names and eight the correct H-Level names. Assuming that chance is .5, the probability of 9/10 successful nets is .0098 and of 8/10 successful nets is .044 according to the binomial distribution. Hence the E-Level grounding successfully transferred to the H-Level categorization.
We also did a control to see whether this outcome depended on some uncontrolled variable rather than grounding transfer. For a set of nets, the E-Level Name learning was skipped; H-Level Name learning followed immediately after prototype learning. None of the ten nets was successful.
We can also count the total number of correct responses instead of the number of correct nets. Since the total number of naming trials is high (2560 for E-Level plus H-Level ) we can use the Gaussian distribution and compute the z value for the difference between the two probabilities. For E-Level naming, the percentage correct is 97% for the grounding transfer test and 15% for the controls (prototype learning only). For H-Level naming, the percentage correct is 92%, compared to 63% for the controls. Here we will compare only the probabilities for H-Level naming. For the difference between the two probabilities, the z value is 30.3 (N=2560; p<.0001), confirming that prior direct grounding is essential for grounding transfer.
4. Discussion
The present results confirm other connectionist models of categorical perception [7]. When trained to categorize, neural nets build internal representations that compress differences within categories and expand them between.
Ours is a "toy" model, but it is hoped that the findings will contribute toward constructing hybrid models that are immune to the symbol grounding problem. Names (symbols) are grounded via net-based connections to the sensory projections of the objects they stand for. Moreover, the grounding of E-Level symbols can be transferred to further symbols through boolean combinations of symbols expressing propositions.
The control simulation showed that direct grounding of at least some names is necessary. We grounded the names of the four E-Level geometrical shapes directly in their retinal projections. The same retinal projections then also activate the new H-Level name, "symmetric," through their indirect grounding. Circles and squares activate some common categorical representation in the hidden layer that in turn activates "symmetric"; rectangles and ellipses activate "asymmetric."
The conditions that lead to grounding transfer require further simulations and analysis. E-Level naming proved sufficient for grounding transfer in most of the nets (80%). Thirty percent of the control nets were likewise able to transfer grounding to the H-Level names probably because compression/separation induced by their training in e-level categorisation and naming reduced the variability in the hidden layer. This can be tested with further randomised and biased control conditions.
During the prototype-based categorization, the nets learn to produce four separable hidden representations for each of the categories (64 shapes in each), with very similar activation patterns within categories and very different ones between. In addition, there is already some compression of the symmetric and the asymmetric shapes at the prototype level. These "head-starts" in similarity space may explain how some of the nets managed to master the H-Level naming without being taught the E-Level naming: They already had the categories, just not yet their names. And so it may well be with many categories; random seeding is an unlikely model for the initial conditions of biological categorization.
Some categories will already be "prepared" by evolution; others will be acquired on the basis of shared iconic or functional responses, rather than arbitrary naming. But when naming does occur, it will benefit from following these pre-existing gradients or boundaries in similarity space - as long as the requisite new category goes with them rather than against them. This too is a form of grounding transfer.
This explanation is confirmed by the analysis of the naming errors for the E-Level names in the control condition. Nets named only a very low proportion of shapes correctly in this condition (15%) because it gets harder to be right by chance as the number of bits increases. With two possibilities, symmetric/asymmetric, nets can achieve 50% by chance, but with four (circle, square, etc.), chance is 25%. Moreover, the E-Level control errors reveal that circles are often called "circle + square" or simply "square" and conversely. This interconfusability of circles and squares is what one would expect from their close categorical representations.
Our model for categorization and naming can also test hypotheses about the origin of cognition and of language [1]. The proposition describing the H-Level categories in the present simulation ("Circle [is] Symmetric" "Ellipse [is] Asymmetric" etc.) came as a kind of "Deus ex Machina": The E-Level categories could have been acquired by ordinary trial and error reinforcement in the world, through learning supervised by the consequences of categorizing and miscategorizing. This is what we have called learning by Sy. But in a realistic world the symbol combinations on which the H-Level categories were based would have had to come from someone who already knew what was what. This new way of acquiring categories spares us a great deal of sensorimotor toil. The adaptive advantages of this new mode of category acquisition may be the evolutionary origin of language.
References
[1] Cangelosi A, Parisi D. The evolution of a 'language' in an evolving population of neural nets. Connection Science (in press)
[2] Goldstone R. Influences of categorization of perceptual discrimination. Journal of Experimental Psychology: General 1994; 123:178-200
[3] Jacobs RA, Kosslyn SM. Encoding shape and spatial relations: The role of receptive field size in coordinating complementary representations. Cognitive Science 1994; 18:361-386.
[4] Harnad S (ed). Categorical Perception: The Groundwork of Cognition. New York, Cambridge University Press, 1987
[5] Harnad S. The Symbol Grounding Problem. Physica D 1990; 42:335-346
[6] Harnad S. Grounding symbols in the analog world with neural nets. Think, 1993; 2:12-78
[7] Tijsseling A, Harnad S. Warping Similarity Space in Category Learning by Backprop Nets. In: Ramscar et al. (eds.) Proceedings of SimCat 1997: Edinburgh University, 1997