TABLE OF CONTENTS
I. The Coordinate Axes for Measurement
II. Construction of Coordinates for Measurement:
Choosing Basis Functions
A. Decomposition of ERPs by digitizing
B. Decomposition of ERPs into peaks and zero crossings
C. Decomposition of ERPs with analytic basis functions
III. Some Techniques for Constructing Coordinate Systems
A. Decomposition of the ERPs into mean and higher
moments
B. Decomposition of ERPs into sines and cosines
C. Decomposition of ERPs by segmentation
D. Decomposition with the use of spatial analysis
E. Search for families of analytic basis functions
F. Fitting curves and testing the results
IV. Conclusion
V. Summary
Evoked potentials are used for measurement of dynamic events in the nervous system that accompany and are related to defined sequences of behavior. The usual raw data are recordings of potential differences in or around the central nervous system that fluctuate in amplitude over limited time spans during behavior. The purpose of the study is to detect, describe and classify particular states of the brain that underlie normal and abnormal patterns of behavior, especially those involving higher functions such as perception, learning, cognition, and so forth. The basic approach is to measure the recordings of the potential differences in order to express the information in them by sets of numbers. Description, classification, comparison, correlation, etc., by a variety of statistical techniques are all based on the numbers.
This review is concerned with how the information
in recordings is converted into numbers. It is assumed that the reader
has already defined and measured an appropriate sensory, motor, perceptual
or other behavioral event, that he or she has carried out the preliminary
experiments needed optimally to observe and record event-related potentials
(ERPs) generated by the brain, eyes, muscles, skin, nerves, etc. (Barlow,
1973), and that he or she is familiar with the techniques for sampling
(Lopes da Silva, 1976) and digitizing (Walter, 1972) bioelectrical phenomena.
The first section contains a brief statement of the main elements of theory
that underlie the measurement of ERPs, and the second section describes
three general systems of measurement. The third section outlines some procedures
that are useful in decomposing ERPs in various ways, in order to construct
and evaluate particular systems for measurement.
I. THE COORDINATE AXES FOR MEASUREMENT
Description of the particular wave forms of ERPs is usually of secondary importance. The principal aim is to determine the variation of shape within and between sets of ERPs in relation to associated patterns of behavior. However, the quantitative description of that variability by use of the variance in sets of numbers requires that the shapes be clearly characterized and precisely measured.
Most ERPs have highly irregular shapes that are difficult to describe and comprehend, and their shapes vary erratically and often hugely from trial to trial. The two main sources of the variation are the background EEG activity and the changes from trial to trial in the neural mechanisms generating the ERPs. When the experimental conditions relating to behavioral stimulus and response are fixed to the extent possible, the variation in wave form is reflected in the numbers by what can be called uncorrelated variance. When an experimental condition is deliberately changed across trials, the ERPs can be expected to change as the neural mechanisms change, and this introduces an additional correlated variance. A good system of measurement should produce matrices of numbers that preserve as well as possible the correlated variance and minimize the uncorrelated variance. The aim is not to suppress the variance but to partition it most effectively.
The primary step in measuring the form and variance of ERPs is to decompose it into parts. Each part has three aspects. First, it is an elementary curve. These elementary curves are called basis functions. When a selected set of such curves is added together, the sum should closely conform to the shape of the ERP. Second, each part has a set of numbers or coefficients that denote its height, width, rate of change, and other features. Third, each part defines one or more coordinates, and the set of numbers denotes distances along the axes. The number of coefficients in the set of basis functions specifies the dimensions of the measurement space. In this point of view the measurement of each ERP gives a vector in that space.
The basis functions must be chosen so that each one represents a unique feature of the ERP. This means that the basis functions are independent of each other, and the coordinate axes of each one are not parallel to any other axis, although they need not be orthogonal to any other. Each behavioral measure is also represented by an axis. The variation in wave forms of the ERPs and in behavior is represented by the variance of the numbers on each axis. If there is covariance between the ERPs and behavior, the axes of the ERP measurement space should be positioned (by the proper choice of the basis functions) to project strongly onto the behavioral axes in order to display that covariance.
From an alternative point of view the ERP is conceived
as a signal embedded in noise. The signal is asserted to have certain measurable
attributes such as amplitude, latency, frequency, etc. and the aim is to
measure these in the presence of noise. With the use of a digital computer
the experimenter builds a template or filter that is expected to
match the signal in order to identify it in the noise. Unfortunately
the form of the signal is seldom known in advance, and in any case the
form is expected to vary with changes in the behavioral conditions. That
is, the filter must be adaptive to the varying form of the signal.
Furthermore, the adaptive filter consists of the sum of a set of elementary
curves (basis functions) that is fitted to the ERP. Hence in both views
the measurement process consists in curve-fitting, and the first step is
to choose the basis functions, which are the parts of the ERP.
II. CONSTRUCTION OF COORDINATES FOR MEASUREMENT: CHOOSING BASIS FUNCTIONS.
A. Decomposition of ERPs by digitizing.
There are indefinitely many ways to decompose ERPs by the choice of basis functions. One cannot expect to find a coordinate system that optimally partitions the variance without arduous search. The best place to begin is with the simplest basis function, which is the digitizing pulse.
In this approach an ERP is decomposed into a sequence of short-duration time segments. Each segment is fitted with a rectangular pulse that is evaluated by a height and a latency. The ERP is approximated and represented by the sum of the digitizing pulses, each at a different latency. Each pulse represents an axis, and the number of dimensions in the measurement space is equal to the number of time segments.
The main advantage of this approach is the ease of conversion of the ERP into numbers to any desired degree of precision. Moreover, this step is essential to obtain a set of numbers that can be used for fitting curves from other and more complicated digital filters.
The digitized data are deficient in three ways with respect to the purpose of measurement. First, there is no differentiation between signal and noise other than the noise introduced by the digitizing process. Second, the number of coordinates is unmanageably large, and the information they contain is largely redundant. Third, the most crucial, the value on each coordinate axis is determined only by the ERP amplitude in the corresponding time segment. The information relating to rates of change in the vicinity of each digitizing pulse and more so over the entire extent of the ERP is disenhanced.
In most dynamic systems the characteristic frequencies and decay rates are at least as important as the amplitudes reflected in their outputs. The states of activity of single neurons are revealed in part by the time constants of their synaptic and axonal potentials, so one can expect that large systems of neurons manifest their states in the rates of change as well as the amplitudes of the potentials they generate. These rates can only be clearly evaluated if the measurement process employs appropriately long-lasting basis functions.
B. Decomposition of ERPs into peaks and zero crossings.
A common approach to ERPs is the empirical measurement of peaks and zero-crossings. Here one makes a graphic display of an ERP, labels the successive negative and positive crests and troughs as N1, P1, N2, P2 . . . etc., and measures peak amplitudes and latencies (e.g. P300), and the directions and latencies of zero-crossings. The implicit basis function for decomposition is an empirical hump resembling a parabola or a normal density function,and the ERP is viewed as the sum of a sequence of these elementary curves.
This approach is most useful for the preliminary evaluation of ERPs, because it is easy, rapid, and inexpensive. One can treat the ERP as an n-dimensional vector by making n independent measures of its main features that will incorporate much of its variance for statistical processing. It circumvents the excessive dimensionality of digitized data, and to a certain extent it overcomes the insensitivity of the digitizing process to the rates of change of potential, because one can distinguish the crests of slow and fast waves and represent them independently in the data.
The main drawback of this approach is that there is no way to distinguish the two kinds of variance. Moreover, much of the information contained in the ERP is lost from the data, certainly to the extent that the numbers do not allow reconstruction of the ERP. Some of the behaviorally-related variance is retained in the numbers, but how much cannot be determined without the use of alternative systems of measurement. The act of measuring selected peaks and zero-crossings is often made difficult by the tendencies of adjacent peaks to overlap or merge and vanish or to ride on slow baseline shifts that distort their onset and crest latencies. For these reasons the empirical approach should be regarded as a useful but limited preliminary.
C. Decomposition of ERPs with analytic basis functions.
The deficiencies of the digitized data can be remedied by using sets of elementary curves that are called analytic basis functions. These are continuous curves that extend over the entire duration of each ERP and that are defined by an algebraic term or expression containing one or more coefficients.
The procedure for using them has two stages. In the first stage an ensemble average ERP is made over a set of ERPs after digitizing them. The individual ERPs each contain both signal and noise, and averaging decreases the noise in the ERP but does not eliminate it entirely. Then a curve consisting of the sum of a set of analytic basis functions is fitted to the ERP by adjusting the values of all the coefficients. This curve is called a matched filter. The fitted curve is treated as an approximation for the signal, and the difference between the ERP and the curve is treated as residual noise.
It is assumed that the noise differs on successive trials, and that the shape of the signal also differs due to the correlated variance. The shape of the average for the signal must be unlike any of the signals; it is only an estimate for the shape of each one. For example, if one takes the ensemble average of a set of exponential curves with a rate constant that varies randomly on successive trials, the mean curve is not exponential but can be fitted with one to an approximation. In addition to the distortion of the signal, the fitted curve of course contains none of the variance of the ERPs.
In the second stage the matched filter is used to measure the signal embedded in noise in each of the ERPs. A curve from the same equation is fitted to each of the ERPs in the set, or to subaverages of them, by readjusting the coefficients. That is, the filter is made to be adaptive. The variance in the set of ERPs is incorporated into a matrix of coefficients (usually 4 to 10) of the basis functions, and the distortions introduced by averaging may be largely corrected.
This procedure overcomes the three deficiencies in the digitized data. The number of axes in the measurement space is reduced by an order of magnitude or more. Each coefficient is evaluated on the basis of what is happening over the entire duration of an ERP, so that information on both amplitudes and their rates of change is preserved. Most importantly, curve-fitting introduces a structured hypothesis into the measurement process. It asserts on the basis of the ensemble average that particular parts or components such as exponentials or damped sine waves exist in the ERPs. When bursts of background EEG waves are superimposed on the potential related to a behavioral event, and the signal in the ERP is obscured by noise, the basis functions impose a form that is adaptive but cannot be twisted arbitrarily.
More explicitly, the hypothesis is that a neural mechanism has certain stable properties, and the generic character of its neural signals in a set of ERPs is invariant and can be approximated by a curve from an equation. The shape of the ERPs varies from trial to trial partly due to variations in the mechanism, and these variations are expressed in a matrix of the coefficients in the equations of the fitted curves. Also each ERP contains noise contributed by the background EEG. The noise can be expected to distort the values of the coefficients from their putative true values (in the absence of noise) on each trial.
However, a difference will persist between the
fitted curve and the ERP. This residue is rejected, because the set of
basis functions is not established in respect to individual ERPs but to
the ensemble average of a set of ERPs. This rejection is the main basis
for partitioning the variance, with retention only of that part that is
related to the coordinate space for measurement, i.e. the set of basis
functions. The matrix of coefficients will contain less information than
the digitized raw data, but that content should be more richly related
to the neural events underlying the ERPs and therefore to behavior.
III. SOME TECHNIQUES FOR CONSTRUCTING COORDINATE SYSTEMS.
There is a long step between obtaining a graphic display of an ERP and finding a curve that fits it properly. This section deals with some experimental procedures that may be useful for decomposing the wave form of the ERP in order to find a set of basis functions and fit a curve, that is, to measure the ERP. Emphasis is placed on the continuing feedback of the preliminary results of measurement into the experimental situation, so that the conditions of stimulation and recording can be optimized in respect to the measurement process.
A. Decomposition of the ERPs into mean and higher moments.
It is assumed that preliminary evaluation of an ERP has already been completed to determine qualitatively its general shape, variability, and relation to behavior. One should explore the available range of conditions for stimulation and recording and choose a standardized set of conditions that seem optimal for detailed study of the ERP. Within these fixed conditions one should collect as large a set as feasible of ERPs from one pair of recording electrodes, digitize, and make an ensemble average of all of them.
One should not be embarrassed about averaging over 1,000 trials or even 10,000 trials if they are available. The usual mistake is to average too few. Unquestionably "over-averaging" destroys some of the information in the ERPs, including the variance one wishes to relate to behavior. At this stage one may look at the ERP as a carrier of information, and the aim is to remove the modulations in order to measure the carrier in its basal state. The number of trials needed can be determined in two ways. First, a pre-stimulus baseline segment lasting 10 to 20% of the recording duration should be included if possible and appropriate, and this should be flat in the average. Second, the set may be broken into two separate averages, which should not differ significantly.
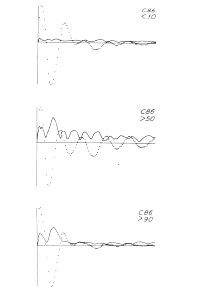
The next step, the mean having been found, is to inspect the variance. The second moment is obtained by plotting the value of the root mean square for each digitizing interval as a function of ERP time. This may give some immediate clues to the structure of a set of ERPs. For example, Figure 1 shows three ERPs, each of which is the over-average (AAEP) of a set of averaged evoked potentials (AEPs) on electrical stimulation of the lateral olfactory tract in a cat while recording the response of the prepyriform cortex. The cat was being trained to press a bar for a reward in response to the electrical stimulation as a conditioned stimulus. Before acquisition of the conditioned response the AAEP has a certain shape and the variance is uniform and unrelated to that shape. In and after the stage of acquisition the AAEP has a different shape, and the variance increases in a way that is closely related to the AAEP. There are obviously two kinds of variance. One is from background EEG activity that is not related to the stimulus, and the other is a modulation of the form of the successive ERPs that occurs during the stage of acquisition of the conditioned response. This would not have been apparent from inspection of the AAEPs alone.
The third moment (root mean cube) plotted as a function of time may be useful for determining asymmetries in the variance, and the fourth moment (root mean quartic) may call attention to trouble spots: outliers consisting of strongly deviant ERPs that may not belong in the set under study. Either the standard conditions have failed to hold and something unusual has occurred on some trials which might be of great interest, or there was an artifact (e.g., a barbiturate spike, or an eye movement). By researching the ensemble of ERPs for those with high negative or positive amplitudes (using the third and fourth moments) at particular post-event times one may be able to improve one's picture of the mean by removal of highly atypical ERPs.
B. Decomposition of ERPs into sines and cosines.
At this stage with a clean mean one may use spectral analysis which is decomposition of the wave shape of the average into a set of sines and cosines over a range of frequencies. There are several reasons for this. First, the ERPs may contain oscillatory components that will require the use of oscillatory basis functions as shown in Figures 1 and 2. Second, the results may suggest improvements in recording procedure to enhance or diminish one or another part of the spectrum by pre-filtering the ERPs, or, if the main frequencies are separated by at least a factor of two, the ERPs may be decomposed into two or more parts by electronic pre-filtering.

Figure 1. The relations are shown between the variance (standard deviation, solid curves) and mean (dotted curves) of the averages (AAEP) of sets of averaged evoked potentials from Implanted electrodes in a cat being trained to press a bar in response to the electrical stimulus used to evoke the potentials. Above: response on C 10% of trials. Middle: response on > 50% of trials (stage of acquisition). Below: response on >90% of trials.

Figure 2. Above left: AEP from a cat with Implanted electrodes (dotted curve) with fitted sum of basis functions (solid curve). Above right: amplitude and phase of the two curves at left after Fourier trans. form by numerical Integration. Below left: polar plot of the Fourier transform. Lower right: dominant and subsidiary components, which are-subsets of basis functions comprising the curve fitted to the AEP. From Freeman, 1975.
Third, spectral analysis may be applied to the background EEG, which is a prime source of the variance of the ERP. If there is a strong periodicity in the EEG, the stimulus repetition rate should be set at an odd multiple of the half length of the period. For example, if the visual cortical evoked potential is recorded in the presence of strong alpha at 10 Hz, the stimulus rate should not be 1/sec (which might lock on to a burst of alpha at any phase) but might be .95 or 1.05/sec.
Another use of the EEG spectrum lies in comparison of it with the spectrum of the AEP. Do the spectral peaks occur at the same frequencies in the EEG and the AEP, and is it desirable or not that they do so? From the standpoint of observability of the single ERP it is not desirable, because the EEG and ERP cannot be separated by band-pass filters. Moreover, such correspondence of spectral peaks happens most often when the amplitude of the single ERP is the same or less than the amplitude of the EEG. Because the only distinguishing characteristic of the ERP is the time of its occurrence, averaging in this case is a necessity. If the ERP and EEG spectral peaks do not overlap, one can use Wiener averaging (Walter, 1969; Hartwell and Erwin, 1 976).
One should consider the point of view that a stimulus
is superimposed on background input to a functional group of neurons, and
that the characteristics of the response to the stimulus should closely
resemble those of the response to the background input. With a strong stimulus
the neural system may respond abnormally, perhaps involving saturation
or partial blockage of the neural mechanism, so that the normal range of
ERP variance is diminished. Then strong stimulation should be avoided.
After all, the aim of analysis is not the suppression of variance but decomposition
and selective removal. The observer should use parametric testing, in which
the stimulus intensity or some other experimental variable is changed in
small steps over a suitable range (see also Section D). For example, one
can obtain a series of clean means and variances over a range of stimulus
intensities or output amplitudes (as appropriate), note the dependence
of wave shape on intensity, and choose for further study a clean mean with
optimal variance, such that there is an optimal covariance with behavior.
Provisionally, it may be useful by adjusting the stimulus intensity to
maximize the nonuniformity of the second moment with respect to ERP time.
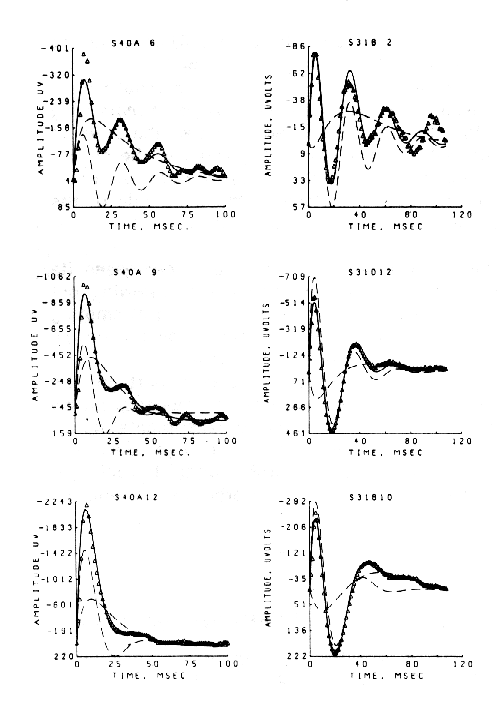
Figure 3. Two sets of AEPs (dotted curves) are shown from the olfactory bulb on stimulation of the lateral olfactory tract (right) and primary olfactory nerve (left). From above to below the stimulus intensity is raised in steps, which changes the amplitude and shape of the AEPs. Solid curves: sum of fitted basis functions. Dashed curves: dominant and subsidiary components.
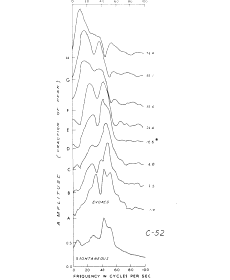
Figure 4. The characteristic effect on AEPs of increasing the stimulus intensity is a spectral shift to the left. The lowest curve is the amplitude spectrum of the prepyriform EEG in a cat. The remaining curves in ascending order are the amplitude spectra of the Fourier transforms of AEPs (normalized to equal maximal amplitude) over a range of increasing stimulus intensity. The asterisk shows the level of the threshold for behavioral responses to the electrical stimulation, at which the amplitudes of single evoked potentials are close to the amplitude of the background EEG. From Freeman, 1975.
Typically the observer has some control over the correspondence between the spectral peaks of the ERP and EEG, because he may change the stimulus rate or intensity and change the spectrum of the ERP. The most likely result of increasing the stimulus intensity is an increase in amplitude of the ERP above the EEG and a decrease in the frequencies of the ERP (Figure 3), which is reflected in a prominent spectral shift (Figure 4). This makes the single ERP much easier to see, but it also decreases its variance. This may be an instance of throwing out the baby with the bath water, because in attempting to observe the carrier, the observer may reduce excessively the correlated variance as well.
This stage reflects an important part of the measurement process, which is the repeated review and updating of the standardized experimental conditions. One clean mean is not an end in itself or a representation of what the ERP "ought" to look like, and its variance should not be arbitrarily diminished prior to partialling.
C. Decomposition of ERPs by segmentation.
The observer should next return for preliminary decomposition to the individual ERPs or to averages of small ensembles in which the second moment is relatively uniform over time and does not covary with the mean, i.e. its variance is mainly due to the superimposed EEG. This is done in three ways, each based on the presence of some stable component in the ERPs and on a provisional idea of the physiological significance of the component (subject to independent verification). The first is blocking into time segments, similarly to the conventional treatment of the electrocardiogram into P-, QRS-, and T-waves that are referred to events in the cardiac cycle. If, for example, the ERPs contain an obvious presynaptic compound action potential prior to the first main peak, this may be split off or removed from the record. However, this procedure should not be used arbitrarily, e.g. to separate a "primary complex" from an "after-discharge" or "ringing," unless these have clearly independent physiological referents.
The second is spectral decomposition. This may be used, for example, to separate a series of "spikes" riding on a slow wave, if these can be referred to corresponding unit activity (Figure 5), but not if the apparent spikes merge with a continuing complex of unknown etiology.
The third is selection of subsets of ERPs in which a distinctive part is present in some and absent in others, whether the difference is induced or occurs "spontaneously." This procedure is based on the premise that some neural circuits may open or close in such fashion that a complex sub-event may appear or disappear, in which case averaging over the entire set would be inappropriate. If the inference is correct, then subtraction of one average from another may reveal the physiological components of an ERP. An example is shown in Figure 6. The procedure should be applied sparingly if at all to individual peaks on a train of such peaks, because one such peak may vanish or reappear due to phase or frequency modulation of two or more overlapping oscillations of potential. The inductive comparison of the ERPs with each other and with the clean mean should help and may lead to the formation of two or more clean means.
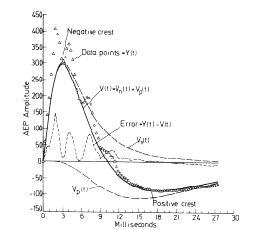
Figure 5. An example is shown of decomposition of the AEP in the turtle cerebellum on electrical stimulation of the peduncle. Solid curve: sum of basis functions. Heavy dashed curves: subsets of basis functions. Light dashed curve: residual difference between the AEP and the solid curve. The successive peaks correspond closely to the pattern of unit firing of Purkinje cells In the region of recording (Bantil, 1974a). From Bantil, 1974b.
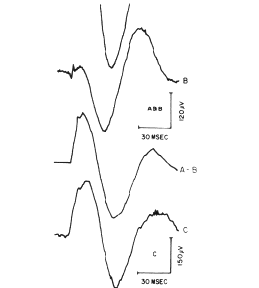
Figure 6. an example is shown at partial decomposition of an AEP.
An electrical stimulus to the lateral olfactory tract In a cat evokes an
orthodromic volley to the prepyriform cortex and an antidromic volley to
the olfactory bulb. The bulbar volley excites Inter. neurons that Inhibit
the excitatory neurons sending axons to the cortex In the tract. The Input
to the cortex Is the orthodromic volley, and a momentary absence of background
Input from the bulb, which Is equivalent to inhibition and evokes an Initially
positive oscillatory wave of activity. Normally these two events are superimposed
(A).
When the tract is stimulated continuously for 3 days at 40
pulses/sec, the orthodromic volley no longer evokes a response, and only
the antidromically mediated component remains (B). When B is subtracted
from A, the missing orthodromically mediated component is revealed (A-B).
When the tract is cut and the missing background activity
is supplied by tetanizing the peripheral cut end of the tract, the orthodromically
mediated component is seen alone (C). From Willey and Freeman, 1968.
D. Decomposition with the use of spatial analysis.
Most of the preceding remarks have been directed toward the analysis of ensembles of ERPs that are collected from one recording site seriatim over time, but they also apply to ensembles of ERPs that are taken concomitantly from multiple recording sites, with or without prior averaging over sequential trials in time. If the sites are chosen reasonably close to each other, the multiple ERPs provide another basis for decomposition.
The ERP arises from the flow of neuronal current across the extracellular fluid in and around the brain. Large numbers of neurons (and glia) are involved, either directly in generating the currents or indirectly in partly controlling those neurons that do. Except for single cell action potentials recorded with microelectrodes the observable fields of potential are generated by functional groups of neurons in cooperative modes of activity. Multiple functional groups coexist and intermingle within each part of the brain. Each group has a characteristic cellular architecture that determines the geometry of its potential field, as well as a characteristic dynamics that regulates the time-varying patterns of its potential field. The potential fields of neighboring and interspersed groups overlap in the extra-cellular fluid and simply add to give the observed potential. However, the contribution of each group is spatially nonuniform, so the ERP wave form determined by the sum of contributions has a different shape at each point over the extent of the whole field of potential.
There are several ways to dissect apart these contributions, including depth recording and laminar analysis; surgical, pharmacological, and behavior manipulation to enhance or suppress the components selectively; correlation of selected components with the patterns of unit activity of single neurons, such as their conditional pulse probabilities with respect to the EEG, poststimulus time histograms, expectation densities, etc.1; analysis of ERPs in response to multiple converging inputs or correlated with multiple outputs; etc. (Freeman, 1975). However, these techniques are not feasible in most studies of ERPs, particularly those in human subjects. In place of them, there are three techniques one can apply directly to spatial ensemble of ERPs.
[*1 The same principles of decomposition and measurement with basis functions apply to statistical even ages of unit activity as well as to field potentials (Freeman, 1975).]
One is factor analysis of the set of ERPs, using location as a stratifying variable to separate the independent wave forms that are generated by contiguous functional groups of neurons. If the potential v(x,t) is recorded (with or without time-averaging) at m points in space x and n points in time t, the analysis yields m factors Fi(t), i = 1, ..., m extending over the duration of the digitized segment. In the results (unpublished) of applying this technique to fields of evoked potential recorded in the olfactory bulb, prepyriform cortex, hippocampus (Horowitz, 1969, 1972), septum (Freeman and Patel, 1968), and superior colliculus (Pickering and Freeman, 1967, 1968), the first 2 or 3 factors have accounted for 95% to 98% of the total variance.
The spatial distributions of the largest factors can be determined by linear regression onto the ERPs. The assumption is made that the record at each point x is the sum of the first two factors F1 and F2 plus noise n(x,t). Then a set of m simultaneous equations is formed in which the potential at each point is the sum of contributions from each factor weighted by a coefficient {GAMMA}.
![]()
The equations are solved for the m values of the weighting coefficients {GAMMA}X1 and {GAMMA}X2. Those values are the basis for making contour plots of the spatial distributions of the two components F1 and F2. The time functions F1(t) and F2(t) are decomposed with basis functions as already described.
This technique may fail for two reasons. One is that the wave forms describing the activity levels of two or more functional groups are not statistically independent. This may be because the groups have similar dynamical properties and respond similarly to common or shared inputs, even though they may be functionally independent. That is, their responses happen to look alike, so that two or more components may be lumped into a single factor. The other reason is that there may be significant time delays in the establishment of a certain pattern of activity across a mass of neurons, due to the slow conduction velocities of input axons, and these delays give rise to the illusion of spreading waves across the tissue. This form of time-dependence and the similarity of the waveforms of multiple otherwise independent groups both tend to confound the factor analysis and cause incomplete and inadequate separation of the components as factors.
The second technique is based on selective averaging. By visual inspection of an array of ERPs it may be possible to locate marginal areas where certain components are relatively clean, and to use these basis functions as factors in equation (1) to analyze the more central and mixed ERPs (Freeman and Patel, 1968). The third technique is to fit basis functions to the ensemble average of the set of ERPs as already described, treat each of them as a factor, and use equation (1) to determine the spatial weighting coefficient l for each basis function. This may allow one to decompose the ERPs into subsets of basis functions with common spatial distributions. The dominant subset can be treated as a signal from one functional group and the others as a mixture of background noise from other groups, in order to focus the analysis on the activity of a major component of the ERP, and to distinguish clearly its variance from the variance of other components.
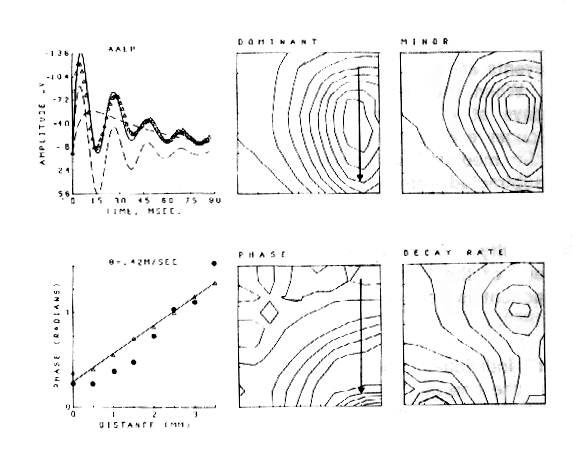
Figure 7. An example is shown of 64 AEPs recorded and averaged concomitantly from the surface of the olfactory bulb on stimulation of the primary olfactory nerve. N = 100. Calibration: 200 microvolts, 50 millisec.
An example is shown for the potential evoked in the olfactory bulb (Figure 7) by stimulation of the primary olfactory nerve and recorded concomitantly on the surface of the bulb with 64 electrodes in an 8 x 8 array (3.5 mm x 3.5 mm). The 64 AEPs differ in shape as well as amplitude with location. The ensemble average (AAEP) in Figure 8a is fitted with a sum of basis functions in two subsets, one that consists of a dominant damped sine wave V1 and the other that is a baseline shift V2. The distributions of amplitudes of V1 and V2 are similar but not identical (Figures 8b and c). The frequency of the oscillation of V1 is everywhere the same, but the decay rate is maximal near the center of V2 (Figure 8f), and the phase (Figure 8e) reflects a delay in the direction of propagation of the afferent axons (arrow). The phase lag (dots in Figure 8d) is consistent with the lag predicted (triangles) from measurements of conduction distance and velocity in the nerve. The example shows how the basis functions are defined in relation to the clean mean, how they are adapted to measure the members of the ensemble, and how the measurements are used to define the spatial distribution and variation in shapes of the AEPs.
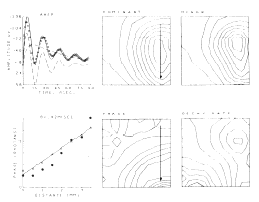
Figure 8. a. Clean mean (symbols) for the AEPs in Figure 7, sum of basis functions (solid curve), and dominant component V1 and subsidiary components V2 (cashed curves). b. Contour plot for V1. c. Contour plot for V2. d. Measured (dots) and predicted (triangles) phase of the dominant component V1. e. Contour plot for the phase of V1. f. Contour plot for the decay rate of V1.
E. Search for families of analytic basis functions.
With these preliminaries taken care of, the main work of decomposition begins. The aim is to select a family of basis functions, such that the sum of a given number or set of basis functions from the family can be fitted as a curve first to a clean mean and then to each of the ERPs comprising it. By this approach the generic shapes of the ERPs are expressed in small sets of numbers that partition and incorporate the variance in an optimal way.
It is advisable to begin by reproducing a clean mean from memory in a freehand drawing to ascertain that its pattern is clearly in mind. Then attempts should be made to dissect the pattern into components, i.e. slow waves, fast waves, oscillation, etc., according to the rules that each component is a curve extending over the entire duration of the ERP, and the sum is an approximate match for the ERP. It is useful at this stage to leaf through handbooks of mathematics and engineering to get some idea of the varieties of curves used to described dynamic processes in many systems, or, better, to have lunch with an engineer or mathematician. It will be necessary to select a family of elementary curves that intuitively seems best to conform to the pattern of the ERP, and to become familiar with the equations used to generate those curves.
The most likely to prove useful is the family of curves comprising the solutions to linear differential equations, that includes pulses, steps, ramps, exponentials, sines, cosines, damped sine waves, and several other elementary wave forms. This may be called the family of linear basis functions. There are several reasons for this choice. The functions are easy to generate, have simple algebraic forms, and are likely to be familiar already. There are numerous electrophysiological systems at the levels of single neurons and masses of neurons in which the dynamics in certain ranges can be described with linear differential equations, and on driving by sensory or electrical impulses each output must then consist of the sum of a set of linear basis functions. Whether a given neural system is operating in a linear way can be tested in accordance with the superposition principle (e.g. paired-shock stimulation in a classical physiological test; see Chapter 2 in Freeman, 1975). Most importantly, many neural systems have two or more ranges of function, only one of which may be linear. Usually this range is for low-amplitude inputs, so that the observer may be able to place the system in the linear range by stimulus control.
At this stage the observer should return to the experiment and carry out careful parametric testing, if it has not already been done, i.e. systematic variation of stimulus interval and intensity (as appropriate), to determine whether a linear range of function exists (Biedenbach and Freeman, 1965), in which additivity and proportionality hold. An example is shown in Figure 9 of the AEPs from single-shock responses recorded in the hippocampus on electrical stimulation of the fornix (Horowitz, 1972). Over a range of low stimulus intensities (a - c) the AEP (for constant N) increases in amplitude without change in its form (proportionality). Over a middle range (d - h) the generic character of the AEP is invariant (approximating a damped sine wave), but the frequency and decay rate of the oscillation change as the initial amplitude increases. At the highest stimulus level (i) shown the AEP changes to a new generic character. The three ranges are linear, near-linear, and nonlinear.

Figure 9 AEPs from the ventral hippocampus at increasing amplitudes of single shocks given to the dorsal fornix. a. 2.5v., N = 6600; b. 3.0v., N = 3600; c. 4.0v., N = 1800; d. 5.2v., N = 850; e. 7.0v., N = 650; f. 9.0v., N = 510; 9. 11.0v., N = 417; h. 15.0v., N = 357; 1. 20.0v., N = 290v. Duration of each AEP Is 125 msec. From Horowitz, 1969.
Alternatively the observer may systematically explore the background conditions for recording. An illustration of this procedure is shown in Figure 10.
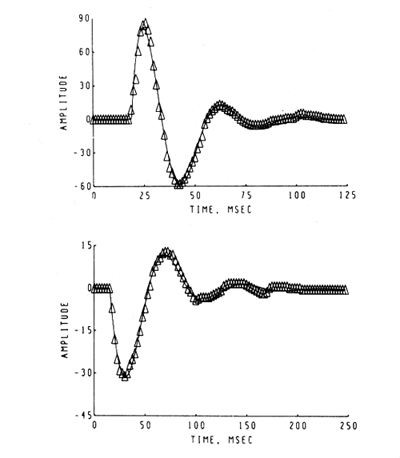
Figure 10. A set of AEPs was taken from a cat with electrodes chronically implanted for stimulation of the optic tract and recording from the superior colliculus. At the time of the upper AEP the cat was placed in a dark box, and thereafter the AEP was taken at the times indicated. The frequency of the AEP increased slightly and the decay rate decreased (Pickering and Freeman, 1967).
The set of AEPs was taken from a cat with stimulating and recording electrodes chronically implanted respectively in the optic tract and superior colliculus. The cat was placed in a light-tight box and the uppermost AEP was taken. Thereafter the AEP was taken at the designated times during presumptive dark adaptation. Control sequences were taken in the same box with illumination to control for the effects on the AEP of habituation, changes in motivation, etc. (Pickering and Freeman, 1967).
The sets of AEPs from the hippocampus and superior colliculus resembled damped sine waves. The degree of conformance was tested by fitting to each one a curve generated from the equation for a damped sine wave. The fit was rather close over the linear (a-c) and near-linear (d-h) ranges for the hippocampal AEPs (for example, lower frame in Figure 11) but not for the nonlinear range (Figure 9,i). The collicular responses conformed only when the initial positive peak (Figure 10) was excluded from the curve-fitting procedure (Figure 11, upper frame). In both sets the frequency, decay rate and phase of the damped sine wave changed in relation to the antecedent variable.
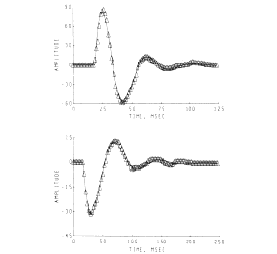
Figure 11. Damped sine wave curves were fitted to the AEPs from the superior colliculus (upper frame) and hippocampus (lower frame) to measure the changes in frequency, decay rate, phase and amplitude. (The curves were fitted by Stan Leung using nonlinear regression.)
If a neural system has a linear or near-linear range, the observer should work within this range at the outset, because the basis functions are then prescribed, and because a thorough study in this range will lay the foundation for an extension into the nonlinear ranges, including characterization of the kinds of nonlinearity and possibly the preferred families of basis functions. Moreover, experience with paleocortical mechanisms indicates that the behaviorally correlated variance in the ERPs is maximal in the linear range. Finally, even if the neural system is not linear according to the superposition principle, the family of linear basis functions may provide a useful approximation.
In the event that a linear basis fails and intuition yields no alternatives, one may fall back on any of a variety of families of orthogonal basis functions (Bessel, Legendre, Tchebyshev, etc.) that may seem optimally to conform to a particular clean mean.
F. Fitting curves and testing the results.
Each basis function is specified by an algebraic term containing one or more coefficients, and the sum of basis functions is generated by the sum of the terms. The next step is to fit the sum of basis functions to a clean mean. This entails finding the proper values of the coefficients by curve-fitting. A number of standard computer procedures are available for this. The most useful procedure is nonlinear regression, in which all of the coefficients (usually 4 to 10) are simultaneously adjusted. A computer center library may be consulted for procedural details (see also Simon, 1972; Chapter 2 in Freeman, 1975).
The criterion for determining the optimal values for the coefficients is minimization of the sum of squares of the differences between the clean mean and the sum of basis functions. Typically one's first attempt yields an unsatisfactory match, and one must try repeatedly while adding new terms or changing existing terms. A successful outcome is when the residue on subtracting the fitted curve from the clean mean resembles white noise or, better still, the appearance of records of an average over control trials on which no event occurred. If this occurs, the ERP or its average has in fact been identified and subtracted out.
A further and essential test of such a fitted curve is then to fit the same curve to each of the ERPs or the subaverages of ERPs that comprise the clean mean. Here the basis functions become adaptive, in that the values of their coefficients are optimized to fit each event or subaverage. If this cannot be done, the most likely reasons are that the basis functions were not properly chosen to reflect the variation, or that averaging was sufficiently destructive to remove certain components, or that one or more components occurred on some trials and not on others. Either a new matching set of basis functions must be sought, or the ensemble must be divided into subsets on the basis of the results on hand. In either case the decomposition of the ERP should now be well under way.
The next test of whether the decomposition is effective lies in study of the relations between sets of coefficients and concomitant measurements of behavioral variables. When the experimental conditions have been fixed, one should observe "spontaneous" variation of the coefficients from trial to trial. The values for each coefficient should be "well-behaved" in the sense that they fall into a unimodal distribution (not necessarily normal), and that one can see patterns of covariation within the matrix of coefficients.
The patterns of covariation between coefficients are best explored with a graph of each pair to determine the ranges and distributions, and the form of the relation. Suitable transformations should be sought to normalize the distributions and to linearize as many of the relations as is feasible. then factor analysis with varimax rotation is used to characterize the patterns (Emery and Freeman, 1969). An example is shown in Table I (Freeman, 1964) of the patterns between eight coefficients from basis functions fitted to the AEPs from the prepyriform cortex of 7 cats, and the rate of work done for food in an ergometer during each averaging period. The covariance matrix for the 7 sets of data was partitioned into interact and intraset matrices, and the latter was converted to a correlation matrix for factor analysis.
The two basis functions fitted to each AEP were damped sine waves; each had coefficients for amplitude V, frequency (transformed to an interval T), decay rate (transformed to the parameter G), and phase P. Rate of work is represented by W. This is a useful form for the end results of measurement.
The next test is to determine whether the same set of basis functions can be applied to the ERPs from several subjects, and whether the same factors emerge from the matrix of coefficients. Here one must come to terms with between-subject variability. The observer may be pleasantly surprised to find the ERPs of considerable variety of shape can be fitted with the same sum of basis functions, though the mean values of the coefficients differ significantly. Alternatively it may be necessary to add, delete, or change terms within the sum. It is reasonable to events in the ERP other than the desired signal. For example, the AEP in Figure 2 has two damped sine wave components. The larger one is a manifestation of the response of an intracortical negative feedback loop in the prepyriform cortex to single shock stimulation, which is manifested by a reverberation between sets of excitatory and inhibitory neurons. This is the signal.
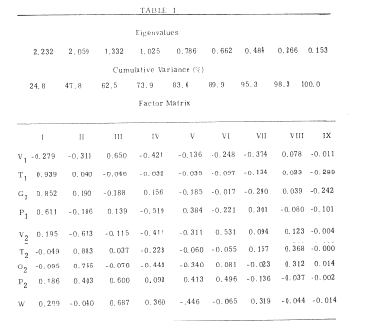
Table 1. An example is shown of the factor matrix for the lumped within-individual variance (excluding the between individual variance) from the 8 coefficients of a curve fitted to 30 AEPs from each of 7 cats. The curve is the sum of two damped sine waves each characterized by an amplitude (V), frequency (T), decay rate (G) and phase (P). Loadings are shown onto the rate of work (W) done by the cats during each period of averaging of the AEP. The main identified factors are I = (-V1´ + T1´ + G1´ + P1), II = (-V2´ + T2´ + G2´ + P2) and III = (V1 P2). The theoretical significance and uses of these factors is described elsewhere (Chapters 6 and 7 in Freeman, 1975). From Freeman, 1964.
The smaller component is the manifestation of a number of complicated feedback loops that include postulate that the same neural mechanisms operate in all subjects under study, although their manifestations in the form of ERPs may undergo distortions in differing ways or be overlapped by subsidiary events in unpredicted ways. If one can identify one or more components that are always present (though variable), one may characterize this subset of basis functions as a signal and treat the other variable basis functions as background "clutter."
There is another way of looking at the problem. The procedure of curve-fitting is essentially the design of a matched filter to detect a desired signal against a white noise background. Any one basis function or any subset of them within a set comprising a fitted curve can be specified as a filter that is matched to a signal. Then the remaining basis functions serve as a filter that is matched to or project onto the intracortical loop, including neurons in the olfactory bulb, nucleus and tubercle, and possibly recurrent projections from the cortical efferent system. The contributions to the dynamics of those longer pathways are not easily distinguishable from each other, but the sum of their effects can be approximated in form by a damped sine wave. This is the clutter. When the cortical dynamics change, both the signal and the clutter vary, and the two filters are adapted (by curve-fitting) simultaneously to reflect the change. To a certain extent the variations in the two filters are correlated, as they should be, because they both involve the intracortical feedback loop.
One can expect that for differing stimulus sites or different subjects the category of the signal will be invariant. That is, the equation for the dominant component is always a damped sine wave, though the values for the coefficient are variable. However, the form of the clutter may vary, meaning that the equation for the sum of the other subsidiary basis functions may vary, as well as the values of the coefficients.
The use of subsidiary basis functions can be regarded as a pre-whitening transformation on the ERP, before the adaptive filter is used to recover the desired signal. In the interest of economy, if the ranges of the frequencies of the filters for the signal and the clutter are sufficiently far apart, the coefficients of the filter matched to the clutter in the clean mean may be fixed, so that only the coefficients of the filter for the signal are varied during adaptation to the signal by nonlinear regression. The variance of the dominant component in relation to behavior may still be optimally preserved.
This principle is familiar to the designers of
radar equipment. The signal reflected from an object such as an aircraft
may be embedded in subsidiary reflections from birds, clouds, hills, etc.
The recovery of the signal is more efficient if filters are designed not
only to recover the desired signal but also to match and remove such clutter
leaving mainly white noise that is the optimal background for detection.
For the observer of ERPs this means decomposing a wave form to identify
a pearl embedded in the oyster.
IV. CONCLUSION
Emphasis has been placed in this review on the desirability of collecting data from ERPs with a large variance, which has not been arbitrarily reduced or collated by strong stimulation, averaging, measurement of peaks and zero-crossings, or band-pass filtering. The aim of measurement is to partition the variance in one or more ways in order best to retain that portion of it that is correlated with behavior and flush out the rest. To this end the uncorrelated variance should be studied in fixed optimally standardized experimental conditions. This includes an evaluation of the background EEG; direct measurement of the ensemble mean, variance and higher moments of the ERPs; and factor analysis of the matrix of measured coefficients in the presence of "spontaneous" variation of the ERPs.
Having done this the observer should be prepared to introduce a systematic change in the standardized experimental conditions, such as in the kind or degree of motivation, level of attentiveness, conditioning in respect to the same or other stimuli, etc. In a new set of ERPs will the clean mean change? Will the same set of basis functions suffice, with changes in the mean values for the coefficients? Will the factor patterns among the coefficients conform to those already found, or will new patterns emerge? Will the new ERPs require a different set of basis functions, either in regard to a presumptive signal or to the clutter? The answers may cause the observer to go back to the first set of data and reformulate the basis functions, choose a new family to explore, or modify the standardized conditions, but with new insight into the ERP as a sum of parts.
The reader may question the worth of detailed analysis
and replication of such fleeting and unstable manifestations of brain activity,
that to friends and colleagues may appear as trivial as the cuneiform tablets
of a dead civilization that after years of study prove to be laundry lists
and tax receipts. (What is it worth to be able to read another language?)
Even if measurement is successful, the results may lead the observer into
realms of statistical and mathematical modeling that are less enticing
than setting patients and animals to interesting behavioral tasks. These
are matters of taste and faith. What is reasonably certain is that the
major circuits of the brain are not likely to be understood solely on the
basis of recording unit potentials by present and foreseeable techniques,
and that the perspectives opened by the analysis of field potentials including
ERPs and EEGs will be essential. Here lies the importance of precise description
and measurement of ERPs. This knowledge must be available as one basis
for the analysis of brain dynamics and cannot be expected to follow logically
from it.
V. SUMMARY.
Neurometrics offers direct access to brain mechanisms that underlie complex mental processes by analysis of the accompanying electrical signs. Such analysis rests on the procedures of measurement whereby complicated wave forms of potential are expressed by numbers for statistical processing. Measurement requires that a coordinate space be set up, and this is done by selecting a family of elementary curves called basis functions. Event related potentials (ERPs) are fitted with a curve consisting of the sum of basis functions to give the numbers.
The simplest basis functions are the digitizing pulse and the empirical peak or hump. These are useful for preliminary evaluation, but they do not convey adequately the information about the rates of change of neural events conveyed in ERPs, and they do not separate effectively the signal from the noise.
The optimal procedure is to average over a very
large ensemble of ERPs in order to minimize the noise, fit a set of analytic
basis functions to the clean mean in order to extract the signal, and then
fit the same curve to each ERP or small subaverages of them in order to
identify the varying signal in the presence of noise. When combined with
a study of the properties of the noise in the absence of the signal (the
background EEG), this procedure approaches partitioning of the variance
in a set of ERPs into parts correlated and uncorrelated with behavioral
events, and it best preserves the correlated part for subsequent statistical
processing, such as by factor analysis.
REFERENCES
Bantli, H. Analysis of difference between potentials evoked by climbing fibers in cerebellum of cat and turtle. Journal of Neurophysiology, 1974, 37, 573-593. (a).
Bantli, H. Analysis of the dynamic behavior of neuron populations in the turtle cerebellum: I. General topological model. il. Lumped circuit model. Kybernetic, 1974, 15, 203-212, 213-225. (b).
Barlow, J.S. (Ed.) Complementary electrophysiological techniques and methods for evaluation of the central nervous system. Handbook of Electroencephalography and Clinical Neurophysiology, Vol. 8B. Amsterdam: Elsevier, 1973.
Biedenbach, M.A., and Freeman, W.J. Linear domain of potential from the prepyriform cortex with respect to stimulus parameters. Experimental Neurology, 1965, 11, 400-417.
Emery, J.D., and Freeman, W.J. Pattern analysis of cortical evoked potential parameters during attention changes. Physiology and Behavior, 1969, 4, 69-77.
Freeman, W.J. Correlation of goal-directed work with sensory cortical excitability. In J. Wortis (Ed.), Proceedings of the Society of Biological Psychiatry (Los Angeles), 1964, 25, 243-250.
Freeman, W.J. Mass Action in the Nervous System, New York: Academic Press, 1975.
Freeman, W.J., and Patel, H.H. Extraneuronal potential fields evoked in septal region of cat by stimulation of fornix. Electroencephalography and Clinical Neurophysiology, 1968, 24, 444-457.
Hartwell, J.W., and Erwin, C.W. Evoked potential analysis: on-line signal optimization using a minicomputer. Electroencephalography and Clinical Neurophysiology, 1976, 41, 416-421.
Horowitz, J.M. Thesis in Physiology: Analysis of a neuronal feedback system of the hippocampus in the cat. 1969: University of California, Berkeley.
Horowitz, J.M. Evoked activity of single units and neural populations in the hippocampus of the cat. Electroencephalography and Clinical Neurophysiology, 1972, 32, 227-440.
Lopes da Silva, F.H. (Ed.) Sampling, conversion and measurement of bioelectrical phenomena. Handbook of Electroencephalography and Clinical Neurophysiology, Vol. 4A, Amsterdam: Elsevier, 1976.
Pickering, S.G., and Freeman, W.J. Variations of the superior collicuius-evoked response in cats. Experimental Neurology, 1967, 19, 127-139.
Pickering, S.G., and Freeman, W.J. Superior colliculus-evoked response in anesthetized cats: space-time characteristics. American Journal of Physiology, 1968, Vol. 214, No. 1, 152-157.
Simon, W. Mathematical Techniques for Physiology and Medicine. New York: Academic Press, 1972.
Walter, D.O. A posterior) "Wiener filtering" of averaged evoked responses. Electroencephalography and Clinical Neurophysiology, 1969, 27, 61-70.
Walter, D.O. (Ed.) Digital processing of bioelectrical phenomena. Handbook of Electroencephalography and Clinical Neurophysiology, Vol. 4B, Amsterdam: Elsevier, 1972.
Willey, T.J., and Freeman, W.J. Alteration of prepyriform evoked response following prolonged electrical stimulation. American Journal of Physiology, 1968, 215, 1435-1441.