We report simulations with backpropagation networks trained to discriminate and then categorize a set of stimuli. The findings suggest a possible mechanism for categorical perception based on altering interstimulus similarity.
Categorical perception (CP) consists of qualitative or quantitative differences in how similar things look depending on whether they are in the same or different categories. Equal-sized physical differences in the physical signals arriving at our sensory receptors can be perceived as smaller within categories and larger between categories. A good example of this is the perception of color. The color of light is determined by its wavelength. The human eye is responsive to wavelengths between 360 and 760 nanometers. Wavelengths produce different color sensations in different regions along this continuum. Differences in wavelength in the range we call "yellow" are perceived as smaller than equal-sized differences that straddle the boundary between yellow and the range called "green" (Berlin & Kay, 1969; Bornstein, 1987). It seems that the wavelength continuum has somehow been "warped", with some regions getting compressed and other regions getting expanded (Harnad, 1987). In the case of color perception, this change in similarity structure appears to be a product of evolution, an inborn property of our sensory systems, and only minimally modifiable (if at all) by experience. We are investigating whether this kind of compression/separation performs a functional role, such as providing compact, bounded chunks (Miller, 1956) with category names that can then be combined into higher-order categories through language (Harnad, 1996; Greco, Cangelosi, & Harnad, 1997).
CP effects also occur in other cognitive modalities. With speech sounds, for example, an acoustic continuum, called the second-formant transition, is transformed into stop-consonant categories like /ba/, /da/, and /ga/ (Rosen & Howell, 1987; Damper, Harnad, & Gore, 1997). Facial expressions have likewise been found to be perceived categorically (Calder et al., 1996; Beale & Keil, 1995). The role of perceptual learning, however, has only recently begun to be investigated in the context of CP, which has been reported with artificial shape categories (Lane, 1965), musical pitch (Siegel & Siegel, 1977), artificially generated "textures" and chick genitalia (Andrews, Livingstone & Harnad, 1997; Pevtzow & Harnad, 1997). In these kinds of experiments, CP occurs when pairwise similarity judgments within and between categories have changed relative to judgments prior to category learning, with within-category compression of perceived similarity and/or between-category separation (Goldstone, 1994).
It is natural to ask what functional role such changes in similarity structure might play in categorisation: Might CP effects provide a clue as to the underlying mechanism of category acquisition? We begin with Harnad, Hanson, & Lubin's (1991, 1995) observation that "CP might arise as a natural side-effect of the means by which certain standard neural net models [..] accomplish learning". In their studies a standard backpropagation network was trained to categorize a set of lines which varied continuously in length. In the present paper we will investigate more closely how such networks learn to categorize further 1D and 2D stimuli. We will test the hypothesis that it is by modifying similarity between internal representations - by "warping" similarity space - that successful categorization is achieved. Changes in perceived interstimulus distances arise from moving hidden-unit representations to the correct side of the category boundary and/or decreasing the weight of some feature dimensions in similarity space.
Harnad et al. (1995) trained a feed-forward backprop network with 12 input units, 3 hidden units, and 15 output units by means of a backpropagation algorithm with a pattern set consisting of 12 patterns. Each pattern is a string of 12 bits which is supposed to represent a "line" of a certain length. Six different coding schemes were used in order to test the effects of the way the lines were represented (table 1).
| discrete | ||||||||
| place | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| thermo | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| coarse | ||||||||
| place | 0 | .001 | .1 | .99 | .1 | .001 | 0 | 0 |
| thermo | .9 | .99 | .99 | .9 | .1 | .001 | 0 | 0 |
| lateral-inhibition | ||||||||
| place | .1 | .1 | .001 | .99 | .001 | .1 | .1 | .1 |
| thermo | .8 | .9 | .9 | .99 | .001 | .1 | .1 | .1 |
Place coding can be considered to be more arbitrary than the thermometer coding as the latter preserves some multi-unit constraints. For example, with thermometer coding a line of length 4 will activate four adjacent units and will share those four bits with a line of length 5, whereas a place coding would not preserve any similarity between these two lines. The thermometer coding preserves the iconicity of the stimuli, i.e. it is structure preserving (Iconic representations are of especial interest in the context of the known tonotopic sensory maps in the neocortex and the thalamus; Kaas et al., 1979; Mcrae, Butler & Popiel, 1987; Obermayer, Blasdel & Schulten, 1991). An extra multi-unit constraint is introduced by having the patterns coarse-coded, such that there is a gaussian spill-over to adjacent units. The lateral inhibition is used to test whether inhibition enhances the boundary between categories.
Before the network is trained to categorize the lines into three categories "short" (lines 1 to 4), "middle" (lines 5 to 8) and "long" (lines 9 to 12), it has to be given an initial discrimination function. The rationale for this is that CP effects are defined as an interaction between discrimination (the capacity to tell pairs of stimuli apart, a relative judgment) and identification (the capacity to categorize or name individual stimuli, an absolute judgment), an interaction whereby the discriminability of objects belonging to the same category is attenuated and/or the discriminability of objects belonging to different categories is enhanced. To induce a discrimination function for the network, `auto-association' is used.
The procedure is as follows. First the net is trained on auto-association. When the mean squared error is below a predefined criterion, the interstimulus distances of the hidden unit activation vectors are calculated for each pair of input patterns using the Euclidean measure. This calculation gives us the discriminabilty metric for the net. After auto-association, the trained weights are reloaded and the net has to do a double task, in addition to performing auto-association task, it must now categorize as well. The category bits in the desired output vector are now set appropriately. As soon as the network has performed to a predefined criterion, the interstimulus distances are calculated again and compared to the pre-categorization values. A CP-effect is then defined as a decrease in within-category interstimulus distances and/or an increase in between-category interstimulus distances relative to the auto-association-alone baseline.
Harnad et al. (1995) report having observed CP-effects for all six kinds of coding, although the thermometer codings seem to generate effects of greater magnitude. They inferred three main factors which influence the generation of CP during the course of learning. First, because the hidden units saturate to 0 or 1, a finite, bounded space forms. In the case of three hidden units, this bounded space is a cube of size one. The hidden unit representations for the patterns move into the extremes of this space during auto-association learning, so as to maximize their distances from one another. This movement, however, interacts with the second factor, the iconicity of the inputs: the less iconic the patterns, the stronger the movements to the outer limits of the hidden unit space. Finally, the dynamics of the backpropagation learning algorithm push the hidden unit representations with a force that is inversely proportional to an exponential function of their distances from the plane separating the two categories.
Harnad et al. suggest that neural networks learn to "sort their inputs into categories imposed by supervised learning through altering the pairwise distances between them [..] until there is sufficient within-category compression and between-category separation to accomplish reliable categorization" (ibid.). Moreover, Harnad et al. claim that the nets don't necessarily stop at a minimal degree of compression/separation, but that they overshoot, thereby producing a stronger CP effect than "necessary". Given the relative simplicity of the backpropagation learning algorithm, however, it seems unlikely that the network is not satisfied to decrease the mean squared error and goes on to make the representations neatly ordered as well.
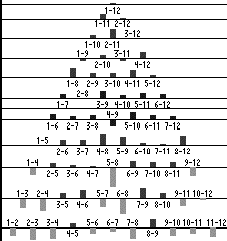
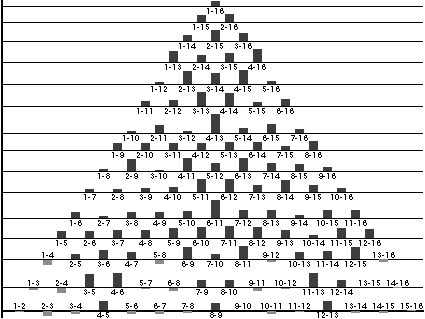
We have replicated the simulations of Harnad et al. (1995). Although our average results are basically the same as in the original study, there are some important new findings. Figure 1 shows the changes in distances between the hidden unit representations after auto-association and categorization for a discrete and a thermometer coding. The distances between each adjacent pair of patterns are shown on the bottom row. Each subsequent row shows the pairwise distances for inputs as length increases (line 1 compared to 2 up to 1 compared to 12).

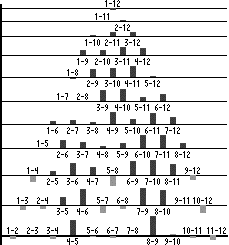
Figure 1: Pairwise distances in hidden unit space. Dark gray is between category and light gray is within category comparisons.
For both types of inputs there is a strong CP effect, with the difference that the place coding shows a bipolar CP-effect (both compression and separation), whereas the thermometer coding elicits a unipolar CP-effect (mainly separation, which is significantly greater for between category comparisons). The latter characteristic was shown to be pervasive over all runs with thermometer coded patterns, whereas with place-coded patterns there seemed to be more variance. A closer look at the network dynamics after auto-association revealed the cause of these effects.
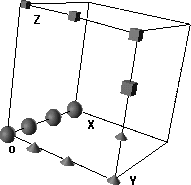
Figure 2: 3D hidden unit space after auto-association for discrete thermometer coded patterns.
Analyses of individual runs show that the presence of CP is determined by the way the hidden unit representations of the input pattern set are organized by the network prior to category learning. Thermometer codings always resulted in a specific type of organization of hidden unit representations, because the patterns have a large overlap (which can be seen by calculating the Hamming distance), forcing the corresponding hidden unit representations to be arranged close to each other in hidden unit space (figure 2). On the other hand, the discrete coded patterns are either othonormal (discrete) or strongly separated (coarse). The final hidden unit configuration after auto-association is as a consequence random, varying from extremely linear separable through moderately separable to very inseparable linearly (figures 3a to c).
So in the case of place codings there are varying degrees of linear separability for each different set of initial weights. The emerging pattern is that starting with the case of extreme linear inseparability there is a high rate of compression-only movement, via the case of moderate linear separability, involving both compression and separation, to the case of extreme linear separability which has a high rate of separation-only movement. The reason is obvious. When the representations are linearly inseparable, they have to move so that the hidden unit space can be partitioned, thereby allowing the two groups of representations can be separated. This always involves moving a representation closer to the others of its kind, hence the compression. At the other extreme the representations do not have to cross the boundary, and the only movement induced is when the boundary plane forces the representations to move away from it, hence the separation. An important thing to note is that in cases of linear separability, the change in the weights other than those from the hidden units to the category node is minimal.
For the thermometer codings (especially discrete and coarse) the pattern is different. Here the same kind of linear separability for each different run is always attained, because the patterns come to be represented close together and in their order of similarity. In most cases the lines are ordered along three adjacent axes of the cubes, starting from the shortest line to the longest, as can be seen in figure 2. The auto-association phase always renders these representations linear separable, but only moderately, as the lines at the boundaries are still relatively close to each other. Categorization training with thermometer codings therefore always shows the same kind of movement in hidden unit space. The closer to the boundary, the stronger the movement away from the plane separating the two categories. Compression effects are usually small here as the representations are already grouped together. They do not have to move closer and, contrary to the report of Harnad et al. (1995), there is absolutely no overshoot at all.
3a. Extreme linear separability. The two groups are separated maximally by being represented on opposite sides of the unit cube.
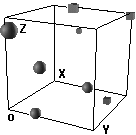
3b.Almost linear separable. The instances of the two classes are not separated completely, but only a small movement of just one object is needed to achieve linear separability.
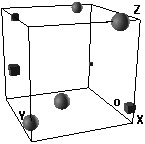
3c. Linear inseparability. The two groups are mixed in the unit cube. For categorization to succeed the respective instances have to travel long distances within the cube.
Figure 3: Varieties of hidden unit representations. Only 8 representations are shown.
In summary, the only condition in which there is always a CP effect is when there is little linear separability between the two groups of patterns. Situations in which there is extreme nonseparability or extreme separability regularly fail to exhibit significant CP effects. However, these conditions are not the interesting ones from a psychological point of view. In categorical perception experiments with human subjects, the stimuli are already discriminable by the subject, but the categories into which they must be sorted are confusable (see Pevtzow & Harnad, 1997, this volume). The objective in these experiments is to see whether mastering the categorization task changes the discriminability of the stimuli. It does not make much sense to train subjects to categorize stimuli that are already far apart from each other in similarity space, such as apples and cars. As these are already so highly discriminable as to be unconfusable, categorization training would not lead to significant changes in how they were perceived. On the other hand, using stimuli that are so confusable that categorization training cannot improve performance will lead to neither successful mastery of the categorization task nor CP. In other words, if stimuli are already so far apart in similarity space that no learning is necessary to partition them correctly, then there is no CP; if they are so near in similarity space that no learning is sufficient to partition them correctly, there is no CP. CP occurs in the "learning zone" in between these two conditions "pre-learning" and "nonlearnability" (Csato et al., submitted). These characteristics are reflected in the neural network counterpart as well.
It appears that a single standard backpropagation network can offer a candidate mechanism for learned CP-effects, but only when the network arrives at a near separable state after auto-association. As this always occurs when the patterns are thermometer coded, the iconicity factor should be included in a mechanism for CP. This factor corresponds to the similarity between patterns, i.e. the number of features the patterns have in common. Hence, the network will show CP-effects only if the patterns are coded in a "meaningful" way. This is tricky, because the modeller is thereby defining the features of the categories. In the current simulations this is not much of a problem as we are using very simple one-dimensional patterns. But when high-dimensional patterns such as pictures of faces are used, we need to find a way to code the patterns without falling into ad-hoc traps. The patterns need to be coded without implicitly predefining the features.
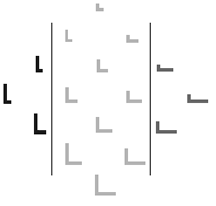
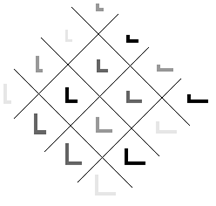
Figure 4: Sixteen two-dimensional patterns subdivided in three categories (denoted by the brightness of the gray color and the separating lines). Note that the categories are unequal in size.
It would accordingly be very interesting to see whether CP effects are generated with more complicated stimuli, such as 2D patterns. We have accordingly run simulations in which two-dimensional 'L'-shaped patterns are used to train the nets. These shapes vary continuously in the length of their vertical and horizontal arms. The results show that with more complicated patterns linear separability of hidden unit representations after auto-association plays a much more crucial role.
The first set of 2D patterns consists of 16 'L'-figures drawn on a grid of 10 by 10 pixels. Each figure has a vertical and a horizontal line meeting in the bottom left corner. The maximum length of the lines is 5 bits. Figure 4 shows a diamond-like setup of the figures, starting with the smallest "L"-shape on the top to the largest one on the bottom. Each layer shows figures that differ from their neighbours in just one colored pixel. The patterns were coarse-thermo coded, so as to preserve multi-unit constraints, and subsequently normalized to improve convergence speed and ratio. We used a standard backpropagation network with 121 input units, 3 hidden units, and 123 output units of which 2 units coded the categories; the net was trained using the procedure outlined previously.
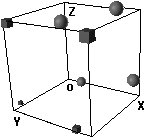
After the auto-association phase the hidden unit representations are always arranged gridwise according to their pairwise similarity (figure 5a). Hence, the only task to be performed by the net during the categorization phase is to rearrange this grid of representations so that there is enough separation between the classes to make error-free categorization possible, but at the same time making sure that the instances are not so close together as to be indiscriminable.
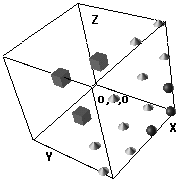
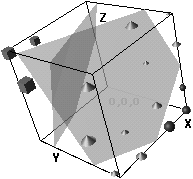
Figure 5: Hidden unit representations. The cubes in the lefthand upper corner correspond to the small category on the left of figure 4. The cones are the large category and the spheres (bottom righthand corner) are the other small category. Also shown in b. are the two boundaries separating the categories. Note that the cubes have been pushed towards the other end of the cube as compared to the auto-association phase.
With the categorization scheme of figure 4 it is obvious that the hidden unit representations are already linearly separable after auto-association. Indeed, after categorization the grid has been stretched out while preserving the pairwise similarity (figure 5b). It can be seen that one of the smaller categories is pushed towards the end of the cube, while the other category stays in place, but gets a bit of compression. This effect persisted through the simulations and accordingly reflected in the CP-effect: separation between the classes, with compression only in the one small category that stayed in place. The distance between the three classes of stimuli, as shown in table 2, indicates that the distance between classes II and III is larger than the one between I and II, which might explain why class III is always the one being pushed away; it is the one closer to the large class II.
| I-II | II-III | I-III |
| 1.68 | 1.58 | 2.17 |
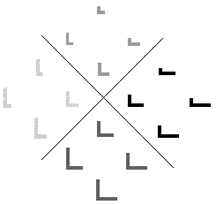
Figure 6: Another categorization scheme consisting of four equal-sized categories.
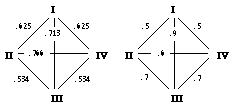
With another classification scheme the network may perform differently. Using the scheme of figure 6, which still uses the linear separability of the hidden unit representations, we have 4 equal-sized categories, each of which contains instances differing from each other in a maximum of two pixels. For this type of categorization scheme we used 2 more output units and 4 hidden units. The simulations showed strong bipolar CP-effects (figure 7). A possible explanation for this persistent bipolar CP-effect is the measure of the distances between the four classes prior to categorization learning (figure 8). Classes II and III are both the same distance to classes I and IV, respectively. The distance between II and III is of similar magnitude to the distance between I and IV. If we look at the relative changes in distance (figure 8), we see that the classes now all have almost the same distance from each other (maximum separability).
To analyse further the crucial role of linear separability, we did another series of simulations with a classification scheme in which the categories were arbitrary ones (see figure 9). We know that the auto-association phase always arranges the hidden unit representations in a grid according to the similarity between them, so if the categories are such that the representations have to be rearranged, then this will be very hard for the network. Indeed, only 30.8% of such networks converged. The networks which succeeded showed only a separation effect, which is not surprising, as the representations have to move relatively large distances in hidden unit space. Backpropagation may be too weak to master such hard learning tasks without using many more hidden units, but our results could also mean that categorization tasks become much more difficult once the network cannot make use of the similarity between the stimuli.
We concluded on the basis of the simulations with one-dimensional input patterns that a potential mechanism for CP may be based on the following factors: (i) iconicity of the internal representations, (ii) movement of internal representations to obtain linear separability, (iii) maximal inter-representational separation, and (iv) inverse-distance forces at the category boundary (see also Harnad et al. 1995). In particular, we have stressed the iconicity of the input patterns, which is closely related to the amount of linear separability among the hidden unit representations. Iconicity constrains the network's tendency to seek maximal inter-representational separation.
It has been shown for both 1D and 2D stimuli that their iconicity induces a similarity preserving structure in their hidden unit representations. As a consequence, categorizations which are based on the similarity between the stimuli are always much easier to learn than categorizations which are orthogonal or contrary to these similarities. We have seen how categorization training moves the internal representations to the correct sides of the boundaries and how the similarity between the representation are warped at the same time. Related to this similarity/iconicity-based representational mechanism is the presence and strength of CP-effects. CP-effects usually occur with similarity-based categorization, but their magnitude and direction vary with the set of stimuli used, how this set of stimuli is carved up into categories, and the distance between those categories.
Beale, J.M. and Keil, F.C. (1995). Categorical perception as an acquired phenomenon: What are the implications? In L.S. Smith and P.J.B. Hancock (Eds.). Neural Computation and Psychology: Workshops in Computing Series. London: Springer-Verlag, 176-187.
Berlin, B. & Kay, P. (1969) Basic color terms: Their universality and evolution. Berkeley: University of California Press.
Bornstein, M. H. (1987) Perceptual Categories in Vision and Audition. In: Harnad (1987).
Calder, AJ, Young, AW, Perrett, DI, Etcoff, NL, Rowland, D. (1996) Categorical Perception of Morphed Facial Expressions. Visual Cognition 3: 81-117.
Csato, L., Kovacs, G, Harnad, S. Pevtzow, R & Lorincz, A. (submitted) Category learning, categorization difficulty, and categorical perception: Computational and behavioral evidence. Connection Science.
Damper, R.I, Harnad, S. & Gore, M.O. (submitted) A computational model of the perception of voicing in initial stop consonants. Journal of the Acoustical Society of America.
Goldstone, R. L. (1994). influences of categorization on perceptual discrimination. Journal of Experimental Psychology: General, 123, 178-200.
Greco, A., Cangelosi, A. & Harnad, S. (1997) A connectionist model of categorical perception and symbol grounding. Proceedings of the 15th Annual Workshop of the European Society for the Study of Cognitive Systems. Freiburg (D). January 1997: 7.
Harnad, S. (ed.) (1987) Categorical Perception: The Groundwork of Cognition. New York: Cambridge University Press.
Harnad, S. (1996) The Origin of Words: A Psychophysical Hypothesis. In Velichkovsky B & Rumbaugh, D. (Eds.) Communicating Meaning: Evolution and Development of Language. NJ: Erlbaum: pp 27-44.
Harnad, S., Hanson, S.J. & Lubin, J. (1991) Categorical Perception and the Evolution of Supervised Learning in Neural Nets. In D.W. Powers & L. Reeker, (Eds.), "Working Papers of the AAAI Spring Symposium on Machine Learning of Natural Language and Ontology".
Harnad, S., Hanson, S.J. & Lubin, J. (1995) Learned Categorical Perception in Neural Nets: Implications for Symbol Grounding. In: V. Honavar & L. Uhr (Eds.), Symbol Processors and Connectionist Network Models in Artificial Intelligence and Cognitive Modelling: Steps Toward Pricipled Integration, Academic Press.
Kaas, J.; Nelson, R.; Sur, M.; Lin, C. & Merzenich, M. (1979) Multiple Representations of the Body Within the Primary Somatosensory Cortex of Primates. Science 204, 521-3.
Lane, H. (1965) The motor theory of speech perception: A critical review. Psychological Review 72: 275 - 309.
McRae, K., Butler, B., Popiel, S. (1987) Spatiotopic and Retinotopic Components of Iconic Memory. Psychological Research, Vol.49, No.4, 221-227.
Miller, G.A. (1956) The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review 63: 81-97.
Obermayer, K., Blasdel, G. G. & Schulten, K. (1991) A neural network model for the formation and for the spatial structure of retinotopic maps, orientation and ocular dominance columns. In T. Kohonen, K. Mikisara, O. Simula & J. Kangas, eds, Artificial Neural Networks, Elsevier, Amsterdam, Netherlands, 505-511.
Pevtzow, R. & Harnad, S. (1997) Warping similarity space in the category learning by human subjects: The role of task difficulty. Proceedings of An Interdisciplinary Workshop On Similarity And Categorisation, Edinburgh, Scotland.
Rosen, S. & Howell, P. (1987) Explanations of Categorical Perception in Speech. In: S. Harnad (1987).
Siegel, J.A. & Siegel, W. (1977) Absolute identification of notes and intervals by musicians. Perception & Psychophysics 21: 143-152.