
Abstract: In innate Categorical Perception (CP) (e.g., colour perception), similarity space is "warped," with regions of increased within-category similarity (compression) and regions of reduced between-category similarity (separation) enh ancing the category boundaries and making categorisation reliable and all-or-none rather than graded. We show that category learning can likewise warp similarity space, resolving uncertainty near category boundaries. Two Hard and two Easy texture learning tasks were compared: As predicted, there were fewer successful Learners with the Hard task, and only the successful Learners of the Hard task exhibited CP. In a second experiment, the Easy task was made Hard by making the corrective feedback during learn ing only 90% reliable; this too generated CP. The results are discussed in relation to supervised, unsupervised and dual-mode models of category learning and representation.The world is full of things that vary in their similarity and interconfusability.O rganisms must somehow resolve this confusion, sorting and acting upon things adaptively. It might be important, for example, to learn which kinds of mushrooms are poisonous and which are safe to eat, minimising the confusion between them (Greco, Cangelosi & Harnad 1997).
Similarity Space Warping
Sometimes nature is generous, and either minimises the interconfusability
by providing natural gaps (we need not worry about how to sort creatures
that are midway between giraffes and zebras as that region of potential
similarity space is empty) or endows us from birth with feature detectors
that sort the continua into discrete categories, creating "virtual" gaps
in otherwise continuous stimulation. Colours and colour boundaries are
examples: pa irs of wave-lengths look more alike when they are in the interior
of a category, such as green, than they do when they straddle the blue/green
boundary (Bornstein 1987).
This selective deformation or "warping" of similarity space has come to be called "categorical perception" (CP; Harnad, 1987). CP effects come in different flavours: within-category compression or between-category separation alone would be "unipolar" CP whereas both together would be "bipolar" CP. Unipolar CP could be relative (compression everywhere, but relatively more within categories, or separation everywhere, but relatively more between categories) or absolute (compression within only or separation between only). ("Anti-CP" -- compression between and separation within -- is logically possible but would be a paradoxical result: getting worse at telling things apart in pairs the better one gets at identifying them individually; such an effect has not yet been reported.)
Innate and Learned CP
Most of the published work on CP focuses on stimuli that we perceive
categorically as a result of mere exposure, without any training; examples
include speech phonemes (Liberman et al., 1957, 1967; Rosen & Howell
1987; Damper & Harnad 1996), colours (Bornstein 1987) and fa cial expressions
(Calder et al. 1996; De Gelder et al. 1997). It is assumed that these perceptual
categories are inborn. The question arises whether CP can be induced by
category learning. Recent reports of CP for face identity (Beale &
Keil, 1995; Le vin 1996) and musical pitch (Burns & Campbell 1994)
suggest an affirmative answer, although the actual learning would have
occurred long before the experiments took place.
Reports of CP arising during the course of learning have also begun to appea r (Andrews et al., 1997; Goldstone, 1994; Goldstone et al. 1996; Stevenage 1997). In the present experiments our interest is in determining the conditions under which similarity space (in this case, discriminability space) is "warped" during the course of category learning: Does CP arise merely as a result of exposure during training or does it depend on the successful learning of the category? (Or, more important, does the successful learning of the category depend on CP?) Does CP arise in all category l earning tasks, whether easy or difficult, or is it playing a functional role in the mastery of difficult categorisation tasks? And if so, what is that functional role?
According to one model for category learning (Harnad et al. 1991, 1995; Tijsseling & amp; Harnad 1997 this volume), CP occurs in the service of category learning: to reliably resolve confusion at the category boundary, where uncertainty is maximal, internal representations of stimuli that are near to or on the wrong side of the category b oundary must be "moved." The movement is manifested as within-category compression and/or between-category separation -- whatever is needed to partition similarity space and generate reliable, all-or-none categorisation.
It follows from this model that CP should occur only when it is needed: In easy, already separable categorisation tasks there should be little or no CP. In unsupervised tasks (mere exposure, with no corrective feedback) there should likewise be little or no CP. Nor should CP occur if c ategorisation is not reliably mastered: CP should only be observed in difficult category learning tasks, and only those that have been successfully learned.
Methods
Participants
78 undergraduates at Southampton University.
S timuli

"Easy" conditions : The two Easy Categories consisted of a microfeature ratio of (i) 0%n/50%m vs. 20%n/30%m (Figure 1, upper) and (ii) 50%n/0%m vs. 30%n/20%m (same as (i) but swapping m's and n's; not shown). These two conditions were mirror inverses of one another (to control for the arbitrary microfeature used). The invariant feature t hat distinguished the categories was 0% of one of the microfeatures in one category vs. 20% in the other. The actual location of all the microfeatures varied from presentation to presentation (except the top and bottom three rows, which were kept identica l in all categories and all conditions, so as to discourage fixation strategies). This categorisation task was predicted to be easy to learn, because it is based on detecting none (0%) vs. some (20%) of a particular microfeature.
"Hard" conditions : Again, mirror inverse controls were used. These required detecting a difference in relative proportions: (iii) 10%n/40%m vs. 30%n/20%m (see lower two textures in Figure 1) and (iv) 40%n/10%m vs. 20%n/30%m (not shown). The invariant this time was 10% vs. 30% (or 20% vs. 40%). Instead of some vs. none, this required distinguishing less and more and was hence predicted to be harder.
Procedures
The experiment consisted of three phases:
(1) Pre-Training Discriminability Measurement : A set of inputs
was presented in triplets to our experimental participants (Ps) so that
we could measure how hard it was to tell them apart before training.
(2) Categorisation Training : Ps were next trained to sort the
stimuli (alone now, ra ther than in pairs) into named categories through
trial and error with corrective feedback after each trial. All Ps had a
total of 200 training trials.
(3) Post-Training Discriminability Measurement : Condition (1)
was repeated to test whether t he training had produced any change in Ps'
capacity to tell apart pairs when they fell in (what would after training
have been learned to be) the same or different categories.
There are several ways to measure discriminability; we used a variant of the standard ABX method used in most CP work (Liberman et al. 1957) in order to force Ps to consider all three stimuli rather than just the last two. The set of stimuli is sampled in triplets (A, B, X) presented one after the other. The first (A) and the sec ond (B) stimuli are always different from each other. On each trial Ps must indicate whether the third stimulus (X) was the same as the first (A), the second (B), or neither (C). The combinations, tested in equal proportions, are ABA, ABB, and ABC. Before training, there are presumably no categories. After training, A and B might either be in the same category or in different categories; ABX then provides a comparative measure of between- and within-category discriminability. Because it occurs both before and after training, it is possible to measure expansion/compression, relative to learning (CP). (The data from the ABC trials that were a hybrid of between and within were discarded.) Note that (1) and (3) are measures of relative judgement: pairs of stimuli are tested to see how well Ps can tell them apart. Categorisation (2) is a measure of absolute judgement: single stimuli must be identified using their unique category name (Miller 1956).
CP effects are measured as interactions betw een absolute and relative judgement by comparing discriminability/similarity before and after training. Each learning condition had two categories: Ps were told that they would view computer textures generated by two different graphic artists, "Percy" and "Quincy," and that their task was to learn, by trial and error, the "style" of each artist, until they could tell whether any texture presented was the work of Percy or Quincy. Each P participated in only one of the four learning conditions (2 Easy, 2 Ha rd).
Following the overall paradigm described above, Ps were tested on (1) ABX discrimination first. Each of the three stimuli was presented for 1000 ms with an ISI of 1000 ms. A practice block of ABX discrimination trials was followed by two 18-trial test blocks. After a rest came (2) 200 training trials in 10 blocks of 20, with each stimulus appearing for up to 1000 ms (shorter if P responded sooner); each response (key press) was followed after 50 ms by feedback (e.g."YES, Quincy" or "no, PERCY"). T he categorisation training was followed by (3) ABX discrimination. There were two 18-trial test blocks, each preceded by a refresher block of categorisation (2).
Results & Discussion
No differences were found between the mirror versions of the two Easy conditions or the two Hard conditions (F(1,36) = .001, p=.97; and F(1,38) = .027, p=.87, respectively), so their data were combined into one overall Easy and one Hard condition. The learning curves for categori sation appeared, upon inspection, to fall into three classes: Learners (monotonically ascending learning curve, terminating at a high intercept), Nonlearners (monotonically ascending learning curve, low terminal intercept) and Nonperformers (learning curv e not monotonically ascending).
We used a terminal intercept criterion to classify the Ps formally as Learners (terminal intercept 0.8; N=48) and Nonlearners (terminal intercept < 0.8; N=19) (see Figure 2) (The data of the Nonperformers: slope < 0.0 (N=11) were discarded on the grounds that they were not following the instructions, otherwise they would not get worse across trials.)
The relative proportion of Learners/Nonlearners proved to differ for the Hard vs. t he Easy conditions (chi square (1) = 12.966, p < .0005) with significantly more Learners in the Easy condition and more Nonlearners in the Hard condition (Figure 3). Note that this datum is based on category learning performance alone; no discriminatio n data are involved. We interpret this difference in proportion of Learners as confirming that the Hard stimuli were indeed harder and the Easy stimuli easier to learn.
Our measure of compression/separation was the ratio of discrimination accuracy aft er (Post) to before (Pre) the categorisation training: The Post/Pre ratio would be 1 if there was no change after training; it would be greater than 1 if there was separation, and less than 1 if there was compression.
For the Learners in the Hard condition, the Post/Pre accuracy ratio between categories was significantly greater than within categories (F(1,16) = 4.53 p <.05), whereas the Learners in the Easy condition showed separation everywhere, within and between, meaning they improved at both ty pes of discrimination after training. Learners in the Hard condition got worse at telling apart members of the same category and better at telling apart members of different categories (Figure 4.). These data support the hypothesis that stimuli that are more similar and hence harder to discriminate cause more confusion at the category boundary, which then calls for CP. No CP is needed when there is little or no uncertainty at the category boundary.
The absence of CP for Ps in the Easy condition suggests that because the stimuli were readily discriminable to begin with, no change in similarity structure was necessary. In the Hard condition, there was a significant interaction between (1) the within-category vs. between-category factor and (2) the terminal intercept factor (F(1,38) = 4.65, p < .05)). The underlying cause of this interaction was a significant correlation between the final level achieved on the learning task and the degree of separation between categories, as measured by the Post/Pre ratio (r(37) = .394, p = .016; see Figure 5); there was no significant correlation with changes within categories (although the direction of the association is negative; see Figure 5). In contrast, for the Easy condition, there was a signi ficant correlation between final learning level and the degree of separation within categories (r(34)=.38, p=.025) and no change between (Figure 5). We interpret this as follows: In the Easy condition there is already sufficient separation between categor ies to accomplish successful categorisation, hence the only effect of the category learning is some sharpening of within-category differences. In the Hard condition, the between-category differences need to be sharpened in the course of category learning in order to achieve successful categorisation.
Experiment 2
In the first experiment, we found between-category separation for the
Learners in the Hard condition and interpreted it as reducing similarity
across the category boundary. Csato et al.'s (submitted) model predicts
that any uncertainty at the decision boundary will generate CP. Would causes
of boundary uncertainty other than between-category similarity also induce
CP? In the first experiment all the un certainty was caused by stimulus
similarity; in this second experiment uncertainty was induced by reducing
the reliability of the feedback during categorisation training for the
Easy stimuli, making the Easy task more like the Hard one.
Methods < p> Participants
32 undergraduates at Southampton University.
Stimuli
The stimuli were identical to those used in the Easy condition of experiment
1.
Procedures
Experiment 2 used the same procedure as Experiment 1 but 10% noise
was added in the categorisation training phase (2), making the corrective
feedback only 90% reliable. (Ps were informed that the feedback signal
would not always be reliable.)
Results & Discussion
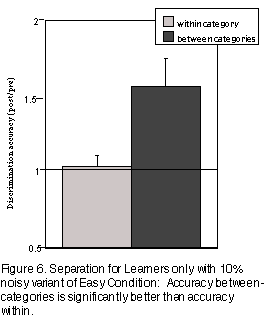
Adding noise to the feedback s ignal during category learning in the Easy task made it more like the Hard task in several respects. The Learners in the Easy 90% condition, like the Learners in the Hard 100% condition, and unlike the Learners in the Easy 100% condition, did show signifi cant separation (F(1,20)= 6.19, p<0.05; Figure 6.). The main difference between the 90% Easy condition and the 100% Hard condition was that the correlation between the magnitude of the CP and the terminal intercept of the learning curve was not present in the 90% "Easy" condition. The data support the hypothesis that uncertainty about the category boundary will result in greater separation across it, although the shift was more pronounced when the uncertainty was caused by stimulus similarity rather th an uncertain feedback about correctness.
In supervised gradient-descent models of categorisation, the deformation of similarity space corresponds to the "movement" of hidden-unit representations to the correct side of a bo undary that separates the categories (Harnad et al. 1991, 1995; Tijsseling & Harnad 1997, this volume). Our findings with the Easy and Hard stimuli confirm that CP occurs when separation is required to accomplish the categorisation, as in the Hard con dition, whereas no CP arises in the Easy condition, where pre training separation is already sufficient to master the task. Our supervised model accounts for the the difference in outcome for the Easy and Hard stimuli in Experiment 1, but it is not clear how it can account for the effects of unreliable feedback with the Easy stimuli of Experiment 2. Goldstone et al. (1996) model separation at the category boundary with competitive learning in an unsupervised network (Goldstone et al. 1996) which recruits units to regions of uncertainty. This can account for the results of Experiment 2. Csato et al. (submitted) have formulated a generalised model that subsumes both the unsupervised and the supervised models as special cases, thereby accounting for the resu lts of both Experiments.
To put these results in a broader context: All computational theories of cognition and all cognitive theories of meaning face the "symbol grounding problem" (Harnad 1990): Computational models consist of symbols and symbol mani pulation rules. If cognition is computation, if thoughts are just strings of symbols, how do the symbols get their meaning? How are they connected to the objects they refer to? Neural nets have been proposed as a mechanism that could provide the connectio n between symbol and object (Harnad 1992, Harnad et al. 1991, 1995) as mediated by perceptual categorisation (Harnad 1987; Harnad 1995).
The analysis of CP is of particular interest, because the grounding of category names (which are really only arbitr ary symbols) in the "shadows" cast on our senses by the objects that the names refer to, by means of pattern-learning filters that can learn to detect and separate them into perceptibly distinct "chunks" through CP, would provide part of the solution to t he symbol grounding problem. A solution to the symbol grounding problem would be extremely important, both in the design of robots and other intelligent machines and in the basic understanding of human and animal cognition.
Some categories are so obvio us that no perceptual learning is needed in order to master them: one exposure coupled with the category name is enough. If the only things in the world were stars and pebbles, then categorisation would be trivial and neither people nor machines would hav e any problem grounding the only two words they would ever have to worry about.
On the other hand, if the only things in the world were two kinds of spheres, completely identical in every respect except that one was a tiny bit bigger than the other, th en if the difference were small enough, two outcomes would be possible: (1) When seen in pairs, the spheres might be discriminable as being of either equal or unequal size, but when seen alone, it might be impossible to categorise them as being of the "bi g" or the "small" kind. Or (2) even discriminating them in pairs might be impossible.
The real world of "blooming, buzzing confusion" whose contents we must all learn to sort and name falls somewhere between these two extremes: between the trivially di sjoint and the unlearnable. And that in-between region where learning is possible was the focus of the present studies. What is the functional role of separation/compression effects in category learning, and how are they related to the difficulty of the c ategorisation and discrimination tasks? Our hypothesis is that CP is a subtle perceptual change in discriminability that occurs in the service of categorisation when the categorisation is neither trivially easy nor impossibly difficult; the magnitude of t he separation/compression effect depends on how much the internal representations of the "shadows" cast by the members and nonmembers of categories have to be "moved" in order to get them on the right side of the category boundary.
The output of perce ptual categorisation is a similarity space that has been deformed in various ways to carve out the parts of the world that we need to act upon differentially and call by different names. Once the names are grounded in perceptual "chunks" which have been l earned the hard way, through trial and error feedback, those names become available for another form of representation and another means of learning new categories: Names can be strung together in the form of propositions that define further categories (H arnad 1996, Cangelosi & Harnad, in prep.). This unique way of acquiring categories is what sets us apart from other species.
Andrews, J., Livingston, K., Harnad, S. & Fischer, U. (1994) Are Concepts Grounded in Categorical Perception? Some Relevant Em pirical Results. Presented at Annual Meeting of Society for Philosophy and Psychology. Memphis TN, June 1994
Beale, J.M., & Keil, F.C. (1996). Categorical perception as an acquired phenomenon: What are the implications? In L. Smith & P. Hancock (Eds.). Springer-Verlag Workshops in Computing Series . Berlin,Heidelberg: Springer-Verlag.
Burns, Edward M.; Campbell, Shari L. (1994) Frequency and frequency-ratio resolution by possessors of absolute and relative pitch: Examples of categorica l perception? Journal of the Acoustical Society of America 96 : 2704-2719
Calder, AJ, Young, AW, Perrett, DI, Etcoff, NL, Rowland, D. (1996) Categorical Perception of Morphed Facial Expressions. Visual Cognition 3 : 81-117
Cangelosi, A & Harnad, S. (in prep) On the Virtues of Theft Over Honest Toil: Grounding Language and Thought in Sensorimotor Categories: Grounding Language and thought in Sensorimotor Categories
Csato, L., Kovacs, G, Harnad, S. Pevtzow, R & Lo rincz, A. (submitted) Category Learning, Categorisation Difficulty and Categorical Perception: Computational Modules and behavioural Evidence. Connection Science.
Damper, R & Harnad, S. (1996) The Auditory Basis of the Perception of Voicing. Procee dings of (ECSA) European Speech Communication Association Tutorial and Research Workshop on "The Auditory Basis of Speech Perception." Keele University. July 19 1996. Pp 69-74.
Damper, R.I, Harnad, S. & Gore, M.O. (submitted) The Auditory Basis of the Perception of Voicing. Journal of the Acoustical Society of America .
De Gelder, B. Teunisse, J-P., & Benson, P.J. (1997). Categorical Perception of facial expressions: Categories and their internal structure. Cognition and Emotion , 11 : 1-23.
Goldstone, R.L. (1994). Influences of categorization of perceptual discrimination. Journal of Experimental Psychology: General , 123 : 178-200.
Goldstone, R. L., Steyvers, M., Larimer, K. (1996). Categorical percept ion of novel dimensions. Proceedings of the Eighteenth Annual Conference of the Cognitive Science Society.
Greco, A., Cangelosi, A. & Harnad, S. (1997) A connectionist model of categorical perception and symbol grounding. Proceedings of the 15th An nual Workshop of the European Society for the Study of Cognitive Systems. Freiburg (D). January 1997: 7.
Greco, A., Cangelosi, A., & Harnad, S. A Connectionist Model for Categorical Perception and Symbol Grounding. Harnad, S., Steklis, H. D. & ; Lancaster, J. B. (eds.) (1976) Origins and Evolution of Language and Speech. Annals of the New York Academy of Sciences 280.
Harnad, S. (Ed.) (1987). Categorical perception: the groundwork of cognition . Cambridge: Cambridge University Pre ss.
Harnad, S. (1990) The Symbol Grounding Problem. Physica D 42 : 335-346.
Harnad, S. (1992) Connecting Object to Symbol in Modeling Cognition. In: A. Clark and R. Lutz (Eds) Connectionism in Context . Springer Verlag
Harnad, S. (1996) The Origin of Words: A Psychophysical Hypothesis In Velichkovsky B & Rumbaugh, D. (Eds.) " Communicating Meaning: Evolution and Development of Language . NJ: Erlbaum.
Harnad, S., Hanson, S.J. & Lubin, J. (1991) Categorical Perc eption and the Evolution of Supervised Learning in Neural Nets. In: Working Papers of the AAAI Spring Symposium on Machine Learning of Natural Language and Ontology (DW Powers & L Reeker, Eds.). Also reprinted as Document D91-09, Deutsches For schungszentrum fur Kuenstliche Intelligenz GmbH Kaiserslautern FRG.
Harnad, S. Hanson, S.J. & Lubin, J. (1995) Learned Categorical Perception in Neural Nets: Implications for Symbol Grounding. In: V. Honavar & L. Uhr (eds) Symbol Processors and Connectionist Network Models in Artificial Intelligence and Cognitive Modelling: Steps Toward Principled Integration. Academic Press. pp. 191-206.
Harnad, S., Steklis, H. D. & Lancaster, J. B. (eds.) (1976) Origins and Evolution of Language and S peech. Annals of the New York Academy of Sciences 280.
Jusczyk, P.W. (1992). Developing phonological categories from the speech signal. In C.E. Fergussonm L. Menn, & C. Stoel-Gammon (Eds.) Phonological development: Models, Research, &a mp; Implications . York Press, Parkton MD.
Kuhl, P. (1987). Perception of speech and sound in early infancy. In P. Salapatek & L. Cohen (Eds.) Handbook of Infant Perception (volume 2 ), New York, Academic Press.
Levin DT. (1996) Clas sifying Faces by Race - The Structure of Face Categories. Journal of Experimental Psychology-LearninG Memory and Cognition 22 : 1364-1382.
Liberman, A. M., Harris, K. S., Hoffman, H. S. & Griffith, B. C. (1957) The discrimination of s peech sounds within and across phoneme boundaries. Journal of Experimental Psychology , 54 : 358 - 368.
Liberman, A.M., Cooper, F.S., Shankweiler, D.P., & Studdert-Kennedy, M. (1967). Perception of the speech code. Psychological R eview , 74 : 431-461.
Miller, G. A. (1956) The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review 63 : 81 - 97
Rosen, S. & Howell, P. (1987) Auditory, Arti culatory and Learning Explanations of Categorical Perception in Speech. In Harnad (1987)
Stevenage, S.V. (1997) Which Twin Are You? A Demonstration of Induced Categorical Perception of Identical Twin Faces. British Journal of Psychology (in pre ss)
Tijsseling, A. & Harnad, S. (1997) Warping Similarity Space in Category Learning by BackProp Nets. Interdisciplinary Workshop On Similarity And Categorisation, Edinburgh, Scotland, November 1997
Young, A.W., Rowland, D., Calder, A.J., Etcof f, N.L., Seth, A., & Perrett, D.I. (1997). Facial expression Megamix: Tests of dimensional and category accounts of emotion recognition. Cognition , 63 : 271-313.