Erhard Bieberich
Institute of Molecular Medicine and Genetics
Medical College of Georgia
1120 15th Street CB-2803
Augusta, GA 30912
[ebieberich@mail.mcg.edu]
Correspondence to:
Dr. Erhard Bieberich
Institute of Molecular Medicine and Genetics
Medical College of Georgia
1120 15th Street CB-2803
Augusta, GA 30912
Phone: 706-721-9113
Fax: 706-721-8272
E-mail: ebieberich@mail.mcg.edu
Keywords: consciousness, Liar paradox, atomism, fractal, quantum
mechanics, computation, Halting problem, Turing machine
Abstract
In human consciousness perceptions are distinct or atomistic events despite being perceived by an apparently undivided inner observer. This paper applies both classical (Boolean) and quantum logic to analysis of the Liar paradox which is taken as a typical example of a self-referential negation in the perception space of an undivided observer. The conception of self-referential paradoxes is a unique ability of the human mind still lacking an explanation on the basis of logic. It will be shown that both classical and quantum logics fail to resolve the paradox because of the particle-like (atomistic) nature of physical events in the moments of perception. The atomistic reality is the only one observed in human consciousness even if, as has been claimed by a number of authors, consciousness arises from a quantum mechanical superposition. However, a computational solution of the paradox can be achieved by embedding quantum registers in a fractal space. The truth values, or q-bit eigenstates, of the separate parts of the paradox correspond to sub-spaces of the fractal. Since a fractal contains the whole in each part a self-referential negation emerges as the experienced concept in each sub-space. Fractal quantum computation is realized by a cNOT-operation with percolation of the control q-bits into sub-spaces of a nascent fractal. In other words, atomism cannot cope with a self-referential paradox but quantum logic gates embedded in a fractal structure can cope. Remarkably, it will be shown that a mind operating on these algorithmic principles will not inevitably be limited by Turing's halting theorem. I suggest a physical mechanism that can deal with our experience of self-referential paradox. Because it is also shown that this cannot be achieved by any previously suggested classical or quantum mechanical operation, the newly proposed mechanism provides a better model than others for an important aspect of the structure of our minds.
Introduction
Three well-known self-referential paradoxes are closely linked with
three inter-related impossibility theorems (Chaitin, 1999). The paradoxes
are 'I, a Cretan, say that all Cretans are liars' (Epimenides), 'who shaves
the barber who shaves everyone who does not shave himself?' (Russell) and
'the first natural number that cannot be named in less than fourteen words'
(a thirteen word definition allegedly due to Berry). The theorems that
link with them are Gödel's incompleteness, Turing's halting theorem,
and Chaitin's information-theoretic formulation of these. In particular,
the halting theorem is of importance for a mechanistic description of the
human mind. It says that no algorithm exists that can always predict whether
a given Turing machine computation will halt (Turing, 1937). Furter, Chaitin
has shown that one cannot prove any theorem whose information content exceeds
that of its axiom system by more than a fixed number of bits (see Chaitin,
1999, for an accessible account of this). A self-referential negation is
fatal for any algorithm since it annihilates its input definitions by its
own computational results. Unprovability and self-referential negation
are particularly baffling since their conception by the human mind raises
the question about whether the mind does in fact operate within an axiomatic
system and therefore can be described by an algorithm embodied in a physical
mechanism. Hence, any model of consciousness, irrespective of whether it
is classical or quantum mechanical, has to be analyzed in the context of
these fundamental theorems.
Penrose (1989, 1994) has famously argued that human minds are not limited
by Goedel incompleteness, hence cannot be Turing machines. If one takes
Chaitin's theorem into account, it is easy to see that Penrose's argument
cannot amount to a proof. Faced with an 'incomputable' problem, people
might subconsciously add 'axioms' to their thought processes until a solution
emerged. 'False' solutions could later be winnowed out by Darwinian mechanisms
selecting for those solutions best fitted to society or to the world. It
is nevertheless possible, however, that Penrose's intuition is valid.
I argue here that examination of the Liar paradox, taken as exemplar for
self-referential paradoxes, allows one to infer a structure for a type
of mind which could escape the limitations of Turing's halting theorem
and hence, by implication, Goedel incompleteness. My suggestion, unlike
that of Penrose, does not entail the introduction of any new physics and
is, I believe, biologically plausible.
My model of the type of mind required has three essential components.
First, it assumes that much brain activity has a fractal structure. This
is uncontentious (see, for example, C.C. King, 1995). Second, it requires
that the 'bottom line' of some of the fractal structure be quantum mechanical
(see Bieberich, 1999, 2000, for further details). Third, it assumes that
this 'bottom line' can take the form of quantum logic gates such as Toffoli
gates. Quantum computation is, of course, a very hot topic at present because
of the hope that it may soon be possible to construct artificial quantum
computers. Accessible accounts of such computation have been provided by,
among others, Milburn (1998) and Lo, Popescu and Spiller (1998). Many 'quantum
computation in the brain' approaches envisage the occurrence of large-scale
quantum coherence in the brain extending across many neurons or even the
whole brain. Mine has the advantage that, being at the basis of a mainly
classical fractal structure, the quantum coherence itself needs to be maintained
for only short periods over areas no greater than part of a single cell
membrane (Bieberich, 1999, 2000). Particularly if envisaged as coherence
between spin of molecules associated with ion channels, it seems likely
that such relatively small-scale quantum structures must arise naturally.
They will therefore have become available for exploitation by evolution
as soon as they arose. The larger scale coherence required by other models
presents greater theoretical problems.
My analysis of the Liar paradox depends on examining its separate, atomistic
components in the context both of the holistic 'field' provided by an undivided,
experiencing consciousness, and of, first classical Boolean logic, followed
by quantum logic. I show that both of these logics are inadequate to account
for our experience of paradox. It emerges, however, that a combination
of quantum logic and fractal topology can accommodate our experience, hence
suggesting that our minds do incorporate these principles. The details
are inevitably somewhat technical, but I hope readers who do not have much
familiarity with these topics will nevertheless be able to follow the argument.
Reference to the figures is probably essential to understanding the text.
There are also appendices describing the basics of quantum computation
and fractal topology for people unfamiliar with them.
Analysis and Discussion
Classical (Boolean) analysis
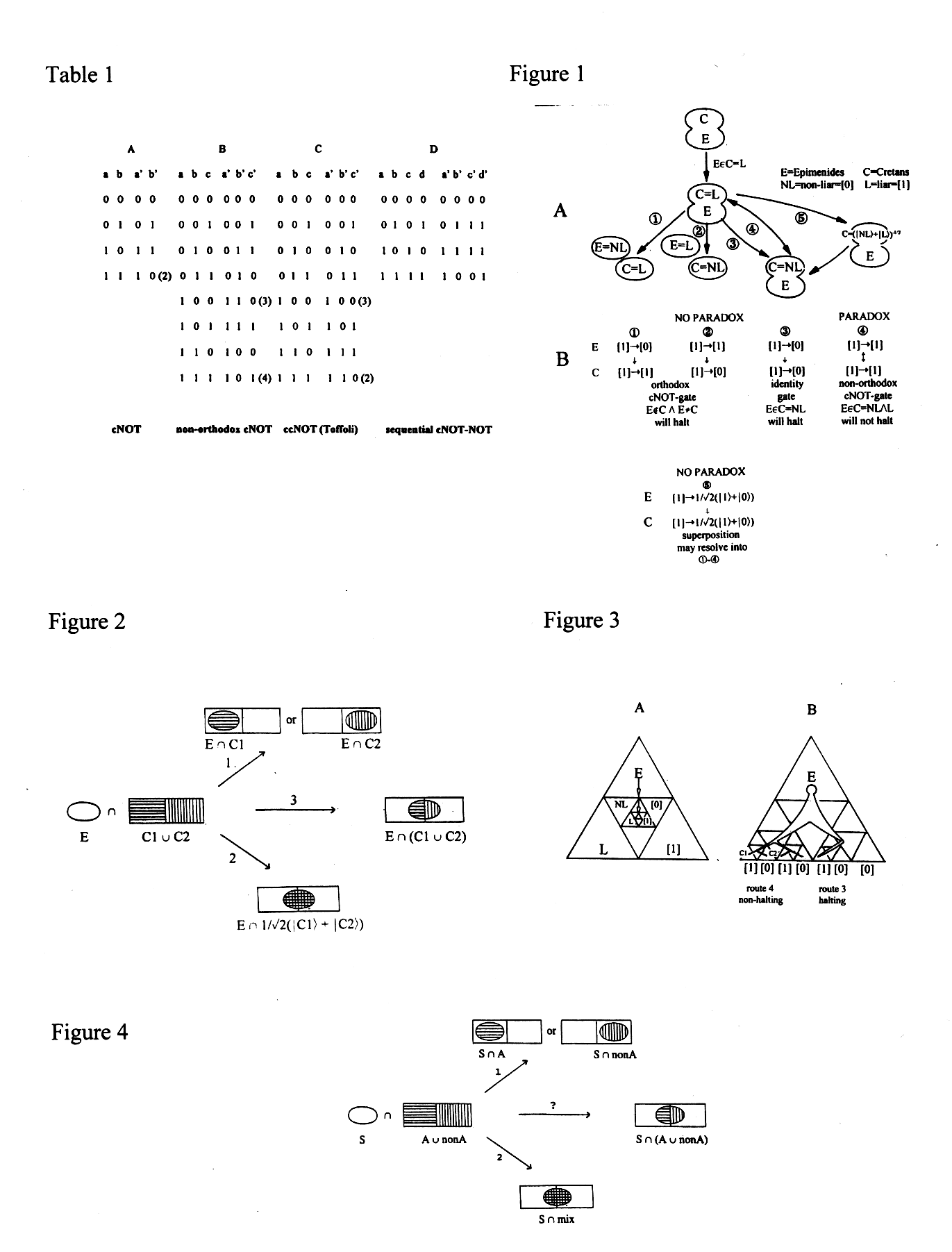
Let's express the Liar paradox in the form, 'I am a Cretan and all Cretans
are liars'. Epimenides' provenance is thus an accessible statement. Here
are two sets of definitions:
(1) E = Epimenides is an element of set C = Cretan or of set NC = non-Cretan
(E is element of C or NC). C may be L = Liar or NL = non-Liar (C = L or
NL). For illustration see Fig. 1; in this figure everything outside of
C is not defined as exclusively either L or NL.
(2) If E = L then a NOT-operation will change the value of each statement made by E.
The Liar paradox can be taken to start with E is element of C and C
= L. Due to a NOT-operation the value of each statement made by E will
change. E now belongs to NC and C = L or NL (Routes 1 and 2 in Fig. 1).
If E is in NC the paradox is resolved by Epimenides being a liar when claiming
to be in C (route 2) or truthful about being NC (Route 1. Note that one
can still suppose, if one wishes, that he may be lying about the propensities
of all Cretans). In contrast, when E does belong to C, the paradox will
be iterated ad infinitum via a combination of Routes 3 and 4. Route
3 on its own would allow termination of the computation as the registers
would simply set to the condition of Epimenides being both C and NL, but
in practice the computation must always be re-started no sooner than finished
due to the route 4-loop. These are the characteristics of a classical or
atomistic computation.
In the literature, a solution of the Liar paradox has been attempted
by avoiding the self-referential negation inherent to the original postulate
(Tarski, 1969; Yablo, 1993). Their approach involves excluding the statement
of E from the truth-value of statements on set C, or in other words, E
'escapes' to a meta-set by temporarily becoming a non-Cretan when making
a statement on C. It has been shown that there are only two ways in classical
computation to restore the state of E being element of C. One is simply
to include a third axiom which says that upon any statement E is no longer
member of C but will be reclaimed as Cretan afterwards. This is equivalent
to route 1, however, the third axiom forces E back on route 4. Hence, there
is no difference to the infinite iteration of routes 3 and 4. Yablo has
tried to remove the self-reference by constructing an infinite series of
Cretan sets with E always making the liar statement on the next following
set that he is not a member of (Sorensen, 1998; Yablo, 1993). However the
Liar paradox, even without immediate self-reference, nevertheless stays
paradoxical when E's statement is repeated infinitely. In these circumstances
we do not know whether Epimenides is a liar or not because we cannot stop
the computation. So the best we can do is to introduce a multi-valued logic:
E is a liar (E = L), or is not a liar (E = NL), or is a state in between
both, a liar and a non-liar (E = L + NL). The latter state takes us immediately
to the next analysis of the Liar paradox discussing Epimenides being both,
a liar and non-liar by means of quantum-mechanical superposition of states.
Quantum logical analysis
If we assign the truth values so that [1] = L and [0] = [NL] to E or
C, it is possible to deal with them in quantum logical cNOT (i.e. controlled
NOT) operation with the q-bit (i.e. quantum-bit) spin values [1] and [0].
Readers wanting a technical description of this quantum logical operation
are referred to Appendix 1. In brief, E and C are two quantum registers
with one control and target q-bit in each register. In quantum logical
operations, spin value changes of the control q-bit are intertwined (i.e.
entangled) with those of the target q-bit. If we start with E housing the
the control q-bit that determines the output of the target q-bit in C,
then the transitions resulting from routes 1 and 2 are compatible with
an orthodox cNOT gate (see Fig. 1). C changes its truth value only if E
stays [1]. E is then not an element of C any longer because being a liar
changes his physical state of being a Cretan (i.e. E is element of NC =
[0] = NL and C = [1] = L, or E is element of NC = [1] = L and C = [0] =
NL. In contrast, route 3 expresses the operation of an identity gate (E
is element of C and both E, C = [0] = NL). Here the truth value is the
same in both registers and there is no lie to be told. Routes 1 to 3 are
not paradoxical so the operation will halt without negation of its own
truth value. Repeat operations will occur only if the orthodox cNOT gate
is re-booted, so to speak, from without.
So far, the computational results of a quantum logical cNOT-gate are
not different from those of a Boolean gate. E may escape the paradox by
becoming an element of the meta-set NC, however, the operation is either
infinitely repeated or E adopts the truth-value [0] = NL for good. The
paradox arises from the combination of route 3 and 4 which looks like another
identity gate, but shows mutual negation of the truth values of E and C
(Fig. 1). This negation is what distinguishes route 4 from the orthodox
identity gate of route 3. It results in a non-halting computation due to
infinite repetition of the negation from within the operation itself. The
necessary quantum logical operation can be implemented by the non-orthodox
cNOT gate described in Appendix 1. As shown in Fig. 1, a gate of this type
can accommodate a quantum superposition of [0] and [1] in each of the two
registers (route 5). The superposition of L and NL itself is non-paradoxical
for as long as it remains 'unmeasured'. A measurement of the truth value
of E and C, however, would be non-paradoxical only if E and C shared the
same truth value within each of their registers, so allowing the computation
to halt via a combination of routes 5 and 3. A combination of routes 5
and 4, on the other hand, will be paradoxical and non-halting in the same
way as the combination of 3 and 4. Recently, Aerts et al. have analyzed
the liar paradox by quantum mechanics reporting the appearance of the truth
values L and NL from a superposition of the two state (Aerts et al., 1999).
However, my analysis by implementation of quantum logical gates has shown
that a superposition of complementary spin a.k.a. truth values cannot be
a solution of the liar paradox without introduction of a previously unknown
non-orthodox cNOT gate.
It might be supposed that the suggested combination of routes 5 and
4 is just a flight of fancy, perhaps analogous to the idea of a perpetual
motion machine forever unrealizable because violating the laws of thermodynamics.
Unlike perpetual motion, however, the non-orthodox cNOT gate does not violate
physical laws. In particular, its reversibility characterizes it as a quantum
logical gate (see Appendix 1). An adequate technical realization is possible
by inclusion of a third, auxiliary q-bit (A) into the logical chain: if
for E: [1] changes to [1], then for A:[1] changes to [0], then for C: [1]
changes to [1]. Note, that the truth value of A is excluded from the set
of accessible (measurable) results. Otherwise the computation will halt
as with a combination of route 5 and 3 resulting in an identity operation.
The exclusion of results from their accessibility does not violate physical
laws but renders the non-orthodox cNOT gate distinct from a sequential
computation as implemented by coupled orthodox cNOT-gates (see Appendix
1).
It is intriguing to note that, if the accessibility of truth value A
= [0] is not permitted, there is no way of discriminating E and C by telling
a lie. In other words, Nature may know a lie in these circumstances but
cannot tell us of Her knowledge through measurement. The concept of a lie
is dependent upon knowledge of the truth. It is thus possible to conclude
that no classical or quantum approach to the solution of the liar paradox
is able to handle the simultaneous existence of a truth value and its negation
in the context of a set of results with only one truth value. Nevertheless,
the simultaneous accessibility of E = L and E = NL in our own minds proves
that this set exists. In order to understand how the set can exist, and
to characterize the nature of a non-orthodox cNOT gate, we need to move
on to a topological approach to the paradox.
Topological analysis
Any classical or quantum measurement of a truth value requires its mapping
into a real space and an at least temporary correlation to the measurement
instrument within this space. This applies to discerning truth values along
with all other measurements. Figure 2 shows that Epimenides' statements
can be represented by a mapping of E into two sub-spaces (C1 = NL and C2
= L) within the group of Cretans. Assuming that any contradiction to the
exclusivity of C's truth value is only temporary, finding an appropriate
operation for resolving the paradox involves mapping Epimenides onto either
C1, or C2, or both together via a superposition of L and NL. But, if the
superposition is measured, Epimenides' space will be split into E mapped
onto C1, or E mapped onto C2, with C1 intersected with C2 = 0 (The respective
product set contains all elements which are both, member of E and C1 or
C2, or member of C1 and C2, respectively. If C1 intersected with C2 = 0
then the intersection set is empty). As before, we either exclude Epimenides
from the space which equals his truth value (routes 1 or 2 in the previous
section), or we include him and enter the paradox (route 3 looping with
4 or 5).
Is there any possibility that E could be in two spaces (C1 and C2) at
the same time without invoking a superposition of L and NL? As it happens,
there is. C and NC can be described as sub-spaces of a fractal, or self-similar
structure (Barnsley, 1993, Peitgen et al., 1992). A brief account for such
spaces is given in Appendix 2. It turns out that the sub-spaces of a fractal
show the following characteristics: C1 unequals C2 and C1 intersected
with C2 unequals 0 (note the different second term here from the one describing
non-fractal sub-spaces given in the previous paragraph). As shown in Fig.
3A each sub-space of a Sierpinski triangle (which is a typical, simple
fractal) contains the other sub-space(s) due to iterative downscaling of
the whole structure into each part.
The process of mapping E can now be pictured as E entering the bottom
triangles of Fig. 3B through two slits (a fractal double-slit). One can
see that mapping E onto C1 or C2 involves simultaneous mapping onto the
other sub-space of the growing fractal. If E is assigned to the central
triangle and controls a cNOT operation on target registers in the bottom
triangle, we have the requisite fractal cNOT gate (see Appendix 1 for more
detail).
Figure 3B shows that the non-halting operation (routes 4 and 5 in the
previous section) is describable as an ongoing mapping of E into two sub-spaces
(C1 and C2) of an emerging fractal. Since E is always in the central triangle,
this implies a repeated copying of the control register into sub-spaces
of the target register accompanying iterative tiling of the Sierpinski
triangle. The control q-bits are multiplying along with proliferation of
the sub-spaces inside the target registers as the computation proceeds.
It should be noted, however, that the total computation does not proceed
by sequential steps but happens simultaneously in each sub-space of the
fractal. The overall picture is of a computation whose different forms
"percolate", so to speak, into different sub-spaces of a fractal tree where
they can proceed independently while nevertheless remaining related to
one another within an all encompassing structure.
A surprising conclusion is that halting and non-halting operations can be discriminated if non-halting requires an equal percolation of E into all sub-spaces of the growing fractal (iteration of route 4). If there is not equal percolation, one computation outgrows the other and hence tends to exclude the other from sub-spaces further down the line. After allowing sufficient time for evolution of the fractal, a discrimination can be made by simply counting the truth values as spin states ([0] = NL and [1] = L) in the bottom triangles (Fig. 3B). The ratio [1]/([1] + [0]) will be 0.5 in case of the non-halting operation whereas it asymptotically reaches 0 otherwise. The first case is identical to the result of a non-orthodox cNOT gate described as an algorithm for the liar paradox in the previous section. An implementation of this algorithm by a fractal can thus decide on whether an operation creates a "true" paradox (route 4) or whether a finalization of the operation occurs (branches of the fractal tree "die out" or route 3).
Penrose has suggested a similar operation for solving the Thue word
problem (Penrose, 1989; see Dewdney for review,1989). In brief, his idea
of a fractal computer (equivalent to the fractal double slit) can substitute
any string of symbols in a finite time, no matter how long they are. This
is the result of a progression toward shorter operation cycles eventually
asymptotically reaching a finite duration for the complete computation.
The fractal cNOT gate is also an operation asymptotically reaching a finite
duration time for a computational result. Similar to Penrose's computer
the halting of a calculation prevents further branching of the fractal
tree. The difference to his model, however, is given by the evolution of
the fractal occurring simultaneously with the computation. Penrose's fractal
computer has an infinite structure a priori whereas the evolution
of the fractal cNOT gate is intrinsically determined by the nature of the
computation (halting or non-halting) itself.
Do fractal gates exist in our brains?
A problem with the fractal gate proposal arises from the fact that there
is no internal evidence in my analysis so far to unequivocally show that
we must posses such gates. As is shown in Appendix 1, for instance, the
output from two orthodox (Toffoli) cNOT gates can mimic the output of my
proposed fractal cNOT gate, at least in the case of halting operations.
More generally, it is always possible to devise some other architecture
which could carry out the same formal operations as the fractal
gate (except in relation to the secondary operation which may solve the
halting problem. However, there is no good evidence that our minds can
in fact sometimes solve this problem). The concept of fractal computation
does have other attractions though, especially as fractality is known to
be involved in so many aspects of brain function. I would like to briefly
mention some other considerations, which suggest that the idea is worth
taking seriously. More detailed accounts are available elsewhere (Bieberich,
1999 a-d).
In this paper, I have tried to analyze a 'self-negation' paradox in
terms of orthodox classical or quantum mechanical models of computations
that might underpin consciousness. In both cases a single event perceived
in a Cartesian space of consciousness is a local and point-like signal,
distinct from any other event once the 'computation' has been accomplished.
Despite tremendous progress in modern neuroscience there are no valid topological
concepts relating a neurophysiological activity to a simultaneous conscious
perception. Hence, it is suggested that the standard concept of point-like
events distributed in a Cartesian space has to be abandoned in favor of
a fractal concept of space containing the whole in each part.
As shown in Fig. 4, classical models based on pinball-like collisions
of neurotransmitters with particular receptors in the nerve cell membrane
will relate an inner observer "S" either to event "A" or "nonA" in a Cartesian
space underlying the topology of neuronal or sub-neuronal anatomy and molecular
morphology. Accordingly, the inner observer will be split into as many
disjoint sub-entities as there are events perceived. Obviously, this model
is equivalent to the mapping of Epimenides onto the sub-spaces C1 or C2
in Fig. 2A. A holistic and undivided perception may be preserved by a quantum
mechanical interpretation as given by a superposition of "A" and "nonA".
A superposition, however, will result in a mixture of indistinguishable
perceptions homogeneously distributed in the perception space. This is
contradictory to our conscious experience of a world consisting of distinct
objects. A resolution by measurement of eigenstates does not provide a
solution of this dilemma since it converts an initial superposition into
a classical distribution of states. This is another apparent paradox, of
a sort.
Resolution of this new paradox seems to require a fundamental change
in our concept of space in relation to consciousness. Recently, two models
have been suggested for embedding consciousness in a configuration space
that is either based on intrinsic contextuality or putative signal non-locality
of entangled quantum states (Aerts et al., 1999; Sarfatti, 1998). The two
models cope with non-local volition of an inner observer by locally acting
on neuronal events. However, the local activity is still bound to the distribution
of the neuronal substrate in a Cartesian space. Accordingly, a correlation
of a consciously experienced perception to a neuronal event has again to
face a topological paradox due to the separability of the substrate. This
correlation will render any computation performed by the human mind as
atomistic as with classical or orthodox quantum mechanical models.
In the present study, the Cartesian concept of space is abandoned and
replaced by a fractal structure containing the whole in each part. A fractal
space underlying the topology of quantum registers may cope with a computational
solution of the Liar paradox and the Halting problem. In addition, mapping
an inner observer onto a fractal perception space is consistent with the
view that computation in the human mind is relying on fractal cNOT gates.
The analysis of the Liar paradox has shown that the classical view of an
atomistic particle distribution in a Cartesian space cannot cope with the
physics required for a description of the human mind. Furthermore, a quantum
mechanical approach will stay incomplete if not combined with a topological
concept for the non-Cartesian distribution of its quantum states. Further
studies are needed on the applicability of the fractal concept to the solution
of other paradoxes arising from the atomistic nature of our percepts.
Acknowledgments: The author is gratefully indebted to Dr. Chris Nunn who gave invaluable support by thoroughly discussing the present study and critically reading the manuscript.
References
Aerts, D., Broekert, J., and Gabora, L. (1999) Nonclassical contextuality in cognition: Borrowing
from quantum mechanical approaches to indeterminism and observer dependence. http://hubcap.clemson.edu/psych/Dialogues/10.0html
Barnsley, M.F. (1993) Fractals everywhere. Academic Press, Cambridge, MA.
Bieberich, E. (1999a) Structure in human consciousness: A fractal approach to the topology of the self perceiving and outer world in an inner space. http://cogprints.soton.ac.uk/abs/neuro/199902004
Bieberich, E. (1999b) Non-local quantum evolution of entangled ensemble states in neural nets and its significance for brain function and a theory of consciousness. http://xxx.lanl.gov/html/quant-ph/9906011.
Bieberich, E. (1999c) Generation of a conscious self in a fractal quantum oscillator (FRAQTOR) J. Consciousness Studies Abstracts Flagstaff conference "Quantum Approaches to Consciousness", p. 23-24. Also accessible at . http://www.bakery.demon.co.uk/flagstaff/abstracts.htm
Bieberich, E. (1999d) In search of a neuronal substrate of the human mind: new concepts from topological neurochemistry. http://cogprints.soton.ac.uk/abs/neuro/199902006
Bieberich, E. (2000) Principles of neural quantum computation and classical communication: Darwinian evolution of the human mind in the quantum dynamical brain. J. Consciousness Stud. Abstracts Tucson 2000, p. 88.
Chaitin, G.J. (1999) The unknowable. Springer, New York, NY.
Dewdney, A.K. (1989) Computer Recreations. Scientific American 12, 140-142.
Faletta, N. (1990) The Paradoxicon. John Wiley & Sons, New York, NY.
Gilburn, G.J. (1998) The Feynman processor. Perseus Books, Reading, MA.
King, C.C. (1995) Fractal neurodynamics and quantum chaos: Resolving the mind-brain paradox through novel biophysics in "Fractals of brain, fractals of mind" (MacCormack, E. and Stamenov, M.I., eds.) John Benjamins, Amsterdam and Philadelphia.
Lo, H-K., Popescu, S., and Spiller, T. (1998) Introduction to quantum information and computation. World Scientific, Singapore.
Penrose, R. (1989) The emperor's new mind. Oxford University Press Inc., New York, NY.
Penrose, R. (1994) Shadows of the mind. Oxford University Press Inc., New York, NY.
Peitgen, H.-O., Jürgen, H., and Saupe, D. (1992) Chaos and Fractals, New Frontiers in Science. Springer-Verlag, New York, NY.
Rieffel, E. and Polak, W. (1998) An Introduction to Quantum Computing for Non-Physicists. http://xxx.lanl.gov/html/quant-ph/9809016
Rosen, R. (1993) Drawing the boundary between subject and object: comments on the mind-brain problem. Theor. Med. 14, 89-100.
Sarfatti, J. (1998) The post-quantum physics of consciousness.
http://www.qedcorp.com/pcr/pcr/pq/pq.htm
Searle, J.R. (1997) Mystery of consciousness. The New York Review of Books, NY, p. 89-93.
Sorensen, R.A. (1998) Yablo's paradox and kindred infinite liars. Mind 107/425, 137-155.
Stapp, H. (1995) Why classical mechanics cannot naturally accommodate consciousness but quantum mechanics can. Psyche 2(5).
Tarski, A. (1969) Truth and proof. Scientific American 6, 63-77.
Turing, A.M. (1937) On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 42, 230-265, correction 43, 544-546.
Vedra, V. and Plenio, M.B. (1998) The Basics of Quantum Computation.
http://xxx.lanl.gov/html/quant-ph/9802065
Yablo, S. (1993) Paradox without self-reference. Analysis 53, 251-252.
Appendix 1
The orthodox and non-orthodox cNOT-gate
The hallmark distinguishing a quantum logical from a classical (Boolean) computation is its reversibility. The classical OR-gate is irreversible (cannot run backwards) since it is impossible to unambiguously infer the input of two bits from their output states (e.g., if output is [1,1] the input can be [0,1], [1,0], or [1,1]). A cNOT-gate consists of a control and target qubit implementing an OR-operation with the input and output spin values [0] and [1] as shown in A (for instructive review see Vedral and Plenio, 1998). If the input [1] of the control qubit equals its output the target qubit changes from [0] to [1] or vice versa. This operation is reversible since the input value of the control qubit can be unambiguously determined from the output of the target qubit (input and output are interchangeable by implementation of the reverse operation). It can be seen as "copy-operation" in the sense that the target qubit with input [0] has the same output [1] as the control qubit (single NOT-operation). The non-orthodox cNOT gate can be constructed from three qubits with [a] as control qubit for [b] and [b] as control qubit for [c] (B). This gate carries out a "copy operation" from [a] on [c] if [1] is given as input for the two qubits (NOT-NOT-operation). In consequence, the output of a non-orthodox cNOT-gate is equivalent to an identity gate. The difference to an orthodox Toffoli gate with three qubits ([a] and [b] are control, [c] is target qubit) is shown in C. The result is also different from an orthodox cNOT-NOT-gate with sequential operation from [a] on [b] and [b] on [d]. This gate can be constructed with four qbits ([a] and [b]: cNOT1, [b] and [c]: identity gate, [c] and [d]: cNOT2) as shown in D. Although the operation resembles B, the sequential cNOT-NOT-gate is not reversible since output and input are not interchangeable. The numbers indicate the routes shown in Fig. 1. Route 1 and 2 are identical due to reversibility of the operation. Route 5 is not shown since only orthogonal results (after accomplishment of the unitary evolution) are denoted.
[Table is presented as Figure "Table 1" in HTML-format].
Appendix 2
Topology of fractal space
A self-similar or fractal structure is generated by iterative mapping
of each point of a compact point set A on a space X into a sub-space Xi
by linear affine transformation (Hutchinson operator, Barnsley, 1993; Peitgen
et al., 1992). The Sierpinski triangle in Fig. 2 can be constructed by
iterative translation of each vertex point along the edges followed by
rotation of the edges by 60°. A downscaling factor warrants a tiling
operation into four equally sized inner triangles forming the sub-spaces
Xi of the fractal. The fractal space is a metric space with
a positive distance function for each point of the sub-sets: X1-X2
unequals 0. However, the sub-sets Ai cannot be separated: A1
intersected with A2 unequals 0. This results in the scale invariance
or self-similarity of the fractal: A = sA with s=scaling factor. As shown
in Fig. 2 each inner triangle contains the whole structure as a downscaled
part. Self-similarity distinguishes the fractal space from any other metric
space.
Legends to the Figures
Figure 1
Analysis of the Liar paradox by classical and quantum logic
Epimenides (E) states "I am a Cretan" (E is element of C) and "All Cretans
are liars" (C = L). Due to the Liar statement routes 1-3 implement a NOT-operation.
E becomes a non-Cretan (routes 1 or 2) and may be a non-liar (NL) or a
liar (L). The operation equals an orthodox cNOT-gate (see Appendix 1) and
halts without entering a paradox. If E stays Cretan the Cretans have to
convert to non-liars (route 3) in order to avoid a paradox. Again, the
operation halts, this time by implementation of an identity gate. However,
if E stays Cretan and non-liar the mere possibility to utter a negation
of a truth-value already creates a paradox. The Cretans oscillate between
C = L and NL ad infinitum (route 4), the operation does not halt.
Route 4 can be implemented by a non-orthodox cNOT gate (see Appendix 1).
The necessary quantum-superposition is indicated by route 5 and can resolve
into the truth-values of routes 1 to 4. Boolean symbols: = and, = or; the
notation (bra-ket) in route 5 is technical and denotes a superposition
state.
Figure 2
Topological analysis of the Liar paradox
Epimenides (E) is mapped onto the space X (C) = C1 in union with C2 (for comparison see Appendix 2). The mapping operation 1 will correlate E either to C1 or C2. The consequence is a splitting of the space in which the Cretans live (equivalent to routes 1 or 2 in Fig. 1). A superposition of E with C1 and C2 is achieved by the mapping operation 2 (equivalent to route 5 in Fig. 1). However, C1 is no longer separable from C2. A simultaneous mapping of E onto C1 and C2 is indicated by the operation 3.
Symbols in set theory: = intersection, = union.
Figure 3
Fractal cNOT-gate
Fractal construction of the space X (C). In A it is shown that Epimenides
= E is mapped into a space which iteratively contains the opposite truth
value as a subspace. As shown in B, the fractal distribution of quantum
states into the sub-spaces of a Sierpinski triangle may be used for implementation
of a non-orthodox cNOT gate. A quantum computation will proceed with E
as control qubit percolating into the target registers (bottom triangles)
by iterative tiling of its sub-spaces. The fractal cNOT-gate can distinguish
a non-halting (equivalent to route 4) from a halting operation (route 3)
by counting the spin values in the target registers (Appendix 1).
Figure 4
Mapping of an inner observer onto a perception space in consciousness
An inner observer (S) is aware of a perception space filled with an
object (A) and all the other objects (nonA). A one-to-one mapping will
split S into S1 aware of A and S2 aware of nonA (1). This is equivalent
to the mapping operation 1 in Fig. 2. If the undividedness of S is preserved
the objects A and nonA will be superimposed but not longer separable (2).
Mapping 3 describes the observation of objects in human consciousness:
S is inseparable but A and nonA are separable.
